Although the interaction between the beam and the fundamental mode is by far the strongest multibunch effect (beam loading), this process can be compensated by choosing an appropriate mode of operation (staggered timing, shaping of klystron pulses etc.). In contrast to this, higher order mode effects depend strongly on mechanical tolerances and require special structure designs to prevent multibunch beam break-up and emittance dilution: Cell-to-cell and structure-to-structure detuning are based on small variations of the cell geometry to decohere the long range wakefield contributions. On the other hand effective HOM damping in long traveling wave structures with either one or few dampers is limited by the existence of trapped modes and the low velocity of energy propagation. Even reduced requirements of damping together with detuning can be fulfilled only with a large number of damper cells. Therefore different concepts of damping with strong impact on the structure design are proposed.

To avoid emittance dilution due to short and lang range wakefields the bunch charge is limited, so that only a small fraction of the cavity energy can be transferred to a single bunch. Therefor, for effective operation, most linear collider studies consider multibunch operation to increase the power conversion efficiency _c=Q_bV_section/t_bP_rf and the filltime efficiency _fill=m_bt_b/(_fill+m_bt_b):

	fill/ns	mb	tb/ns	c	fill
TESLA [1]	515	1130	708	0.98	0.61
SBLC [3]	790	333	6	0.40	0.72
JLC-C [4]	281	72	2.8	0.42	0.42
JLC-X [2]	110	85	1.4	0.54	0.52
NLC [5]	100	90	1.4	0.55	0.56
CLIC [6]	12	50	1.0	0.73	0.81

On the other hand multibunch interactions due to long range wakefields have to be taken into account. The beam loading of monopole modes - especially of the fundamental mode - are by far the strongest long range effects, but they are insensitive to manufacturing and alignment tolerances and predictibaly reach a predictablesteady state. Several modes of operation controlling the klystron timing, phase and/or amplitude are known to compensate this effect sufficiently. In contrast the excitation of fields with higher azimuthal order depend on the offset and tilt of the beam compared to the structure axis. Therefore transverse wakefield effects which cause emittance dilution can only be controlled by structure design, the straighness and the alignment. Active alignment is used to avoid the excitation of transverse wakefields while the rf-structure design intrinsically suppresses the relevant part of the long range wake - either by damping or detuning. Any alignment technique is limited by the straightness of the structure (mechanical structure design), the sensitivity of higher order mode pickups (rf-design), injection errors and the accumulation of alignment errors along the LINAC. Both methods, the suppression as well as the alignmnent allow the requirements for the other one to be relaxed.

The dominant contribution to the transverse wake of one accelerating section is produced by dipole fields and can be written as

with r₁, ₁, r₂, ₂ the offset coordinates of the source and witness charge and s the longitudinal distance between source and witness. The normalized transverse wake function w_T(s) can be split into a resonant term w_r(s) and a transient term w_t(s). The resonant part can be expressed by eigenmodes

.

Usually this equation is modified by damping terms with the time constants =2Q/ to take into account small losses e.g. due to the wall conductivity. As the cutoff frequency of the beam pipe is approximately two to three times higher than the operation frequency only modes below this limit are trapped in the section and can be considered as 'undamped'. Even for higher modes the velocity of energy propagation is typically small compared to c so that the damping time is much higher than L/c (with L = section length). Therefore it is convenient to use this description (together with the corresponding longitudinal component) for beam dynamic simulations of weakly damped structures. For strongly damped structures w_T(s) is directly calculated in time domain.

The requirements for the suppression of the long range wake, derived from beam dynamics simulations, depend on many parameters (such as the bunch charge, acceleration gradient, focussing strength and tolerable emittance growth). Nevertheless for most design studies a rough criterion can be given: for the CLIC [6] and the X-band sections [7] the transverse wake for following bunches has to be reduced by at least by a factor of 100 compared to the peak wakefield. The simulations for the SBLC structure indicate that a factor of 10 is necessary 3, and for TESLA a supression factor of 2 is more than sufficient 8.

The sums of loss- and kick-parameters to a certain frequency f

illustrate the net effect of mode density and strength. Fig.1 gives an impression of the frequency distribution of k and the spectrum of w_T(s). This diagram was calculated for a constant gradient structure with 180 cells very similar to the SBLC section, but it is typical for most disc loaded structures. In the frequency range below 4f₀ about ten separated passbands can be distinguished for individual cells in a periodic approximation. Although these bands are not identical for different cells in a tapered structure, certain frequency ranges can be related to particular bands. In this sense even in aperiodic structures many modes can be addressed by band numbers.

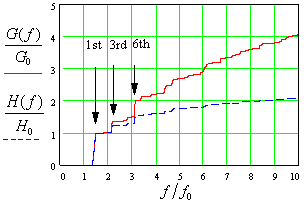
The first step in fig. 1 at f/f_{0 1.3..1.5} corresponds to the lowest dipole band. As most design effort and most HOM calculations were dedicated to this band the step is normalized to one. The absolute values G₀ and H₀ depend on the precise cell shape (e.g. the ratio of coupling hole diameter to wavelength) but they can roughly be estimated by

The peak value of the transverse wake, which is essentially caused by modes of the first dipole band, is approximately 2H₀. This gives a relation for the absolute requirements of wakefield suppression.

	L	Nbunch		max(wt(s))/L#
unit	m	1010	V/Cm3	V/Cm2
TESLA	1	3.6	8101012	471012
SBLC	6	1.1	951015	2.11015
JLX-X	1.5	0.65	131018	801015
NLC	1.8	0.63	131018	801015

^# Contribution of the first dipole band.

Higher Dipole Bands

The contribution of the 2nd, 4th and 5th dipole band to the normalized kick-parameter sum is only a few percent for each. In constant impedance sections (such as CLIC) this contribution is essentially caused by one mode which cannot decohere with other oscillations. Only a continuous cell-to-cell detuning is necessary to decrease the transversal wake for the succeding bunches below 1%. This is already reached with conventionally designed constant gradient sections. Significant steps higher than 10% can be seen for the 3rd band (f/f_02.3) and for the 6th band (f/f_03.2). The effect calculated in [9] for the NLC structure is smaller, but could only be avoided by tapering the iris thickness of the NLC and JLC-X structures to improve the detuning. For the SBLC structure the 'natural' CG detuning is sufficient for the 3rd band, but the synchronous frequencies of the 6th band are too close for all cells. Therefore a slight tapering of the iris thickness is necessary as well.

Very High Modes

The influence of very high modes (above the sixth passband) is neglected for two reasons: the decay time _d=2Q/ decreases at least with ^-0.5 and the spectral power density in a loss free structure decays asymptotically with at least ^-3. The first argument is certainly right for damped structures, but in undamped sections with 100 cells or more the energy dissipation in the walls and the power flux into the beam pipe or through high power couplers does not prevent decay times in the order of or above t_b. The second argument was verified for the SBLC structure by a direct calculation of the transverse long range wake in the frequency range below10f₀. This frequency range is still too small to estimate the exponent of the spectral decay, but a significant drop could be observed. The frequency contribution above the sixth passband (3.3f₀) appears as stationary noise with the rms amplitude 0.01max(w_t) for s>40.

Bunch-to-bunch damping means that the damping time is at least of the order of the bunch repetition time. This is the only method to reduce wake fields in CI structures (more precisely: not detuned structures) but it is also used in tapered structures to ensure - independent from the detuning - that all HOMs are damped. On the one hand a higher order mode needs a quality factor equal or below Q=t_bf/lnd to be damped during the bunch repetition time t_b by the factor d. On the other hand the maximal damping is limited by the velocity of energy propagation and the distance between HOM dampers. The following estimations are based on a simple propagation model. They are valid if the decay length v_gQ/f is large compared to the cell period. With dampers at the structure ends the quality cannot be reduced below Q=/4, where is the HOM filltime. is given for CI structures by L/v_g and for smooth tapered structures can be estimated by 1/(f₊₁-f_-1). However the theoretical Q values are by far not reachable for trapped modes.

Only TESLA with its large bunch distance and small damping requirement is well below this limit. Therefore two couplers at the beam pipes of every nine cell cavity are sufficient for both polarization planes. Nevertheless the detuning of the end cells (due to the beam pipes), their different polarization (due to the coupler polarization) and manufacturing tolerances may cause trapped or tilted field distributions with little energy at the coupler with the matching polarization. As the cell to cell coupling of modes below the cutoff frequency of the beam pipe (TE₁₁₁- and TM₁₁₀-like modes) is large, their field pattern is not very sensitive to this effects. Tilted modes above f_c are either damped by the coupler at the cavity end or the coupler at the next cavity. To "untrap" TE₁₂₁-like modes an asymmetric end cell tuning (with modified cavity curvature) is used [10].

Using several dampers along a section provides stronger absorption, but even with perfect absorbers, the distance between dampers cannot be greater than L_c=2v_gt_b/lnd. (This equation is applicable to tapered structures provided that v_g, the local group velocity, is approximately constant over the length L_c.) For LC projects with small bunch spacing it would be necessary to place dampers every few cells in order to fulfil the requirements for the first pass band. As it is difficult to manufacture and tune sections with a high number of special cells and as real absorbers are less efficient than ideal ones, structures with one damper per cell (for at least one polarization plane) are preferred.

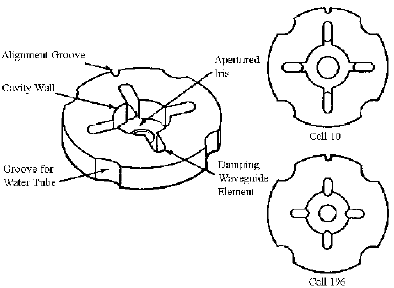
The "HOM free" choke mode cavity [4] in fig. 3 is foreseen for the JLC-C section. The choke is a sharp notch-filter which only traps the accelerating mode inside the cavity. All other modes can propagate out of the cavity without large reflections at the choke. A good broad band absorber is necessary to terminate the outgoing cylindrical wave. Compared to a conventional disc loaded structure the quality of the accelerating mode is reduced by 13% and approximately 13% of its field energy is stored in the choke filter so that the shunt impedance is lowered by 25%. As also the beam loading is also reduced, only 15% more input power is necessary to achieve the same loaded gradient.

For the new CLIC multibunch parameters purely damped structures are being investigated [6]. Therefore either two or four radial output waveguides couple to each cell. The two waveguide version uses T-shaped waveguides which directly couple to the cell. In principle this type of coupler is suitable for both polarization planes, but to avoid asymmetric damping it is turned by 90 degrees from cell to cell. The four waveguide version uses iris coupling - which is more difficult to fabricate - but reduces the additional losses to about 5%. Time domain simulations with perfectly terminated waveguides obtained less than 1% of the single bunch total transverse wake for the following bunches in a frequency range below 4.7f₀.

The interference of several modes in a narrow frequency range can be used to suppress the wake field by detuning. If the frequency spacing of modes is small compared to c/s the sum for the normalized wake can be approximated by an integral

,

with continuous functions for the loss parameter k and the mode density n/. If we consider the contribution of only one band, F() is a narrow function with the center frequency _c. The envelope E(s) of the wake function is given by the magnitude of the Fourier transformation of F(-_c). In the range of a few bunch distances a very good approximation for w_r(s) and F() can be found from the 'uncoupled model' [9]: the parameters and k of the complete (coupled) solution are replaced by the synchronous parameters _c and k_c which can be calculated for the periodic approximation of each individual cell. On a longer scale the oscillations may recohere to some extent and after a very long distance the oscillator phases are randomly distributed which leads to the rms amplitude

_.

Constant Impedance Structures

For conventional disc loaded structures F() is determined by the generic cell geometry, the cell number N and the damping parameter =0.5ln(P_in/P_out). To a good approximation it rises linearly from F(_1c)=F₁k_1c/_1c to F(_Nc)=F_Nk_Nc/_Nc. The envelope is

with A=(F_N-F₁)/(F₁+F_N) and =(_Nc-_1c)/2c. Usually the second term is negligible for the third and later bunches. According to this model the wake of the first dipole band of the SBLC structure (with f_Nc-f_1c=320MHz, F₁/F_N=1.38) is below 5% of the peak value for all following bunches. The calculation of the long range wake by a loss-free, double-band coupled oscillator model indicates that the wake is below the 5% level for the next 120m and recoheres to 30% after 132m.

Detuned Structures

Three cavity parameters are used for the JLC-X and NLC sections to tune the accelerating mode and to detune the first and some higher dipole bands. As mentioned before the iris thickness is used to spread the synchronous frequencies _c of the third and sixth dipole band. Therefore the pairs of cell and iris radii are uniquely defined for every group velocity v_g of the accelerating mode. In contrast to CI structures the group velocity profile is not adjusted with respect to the accelerating mode but to obtain a particular frequency response F(). One idea was to produce minimas of E(s) |sin(s)/(s)| at the positions of the next bunches (s=nt_b/c) but the present proposals use a truncated Gaussian distribution

/_c is essentially determined by the structure parameter =ln(P_b/P_a) and / is set so that the envelope function for the second bunch drops below 0.01E(0). Calculations for the NLC structure based on coupled oscillator models show that the envelope function resurges after L_r10m above the 1% level. To verify that the detuning works as expected, a full scale prototype of the detuned NLC structure has been build and was measured in the ASSET test facility [11]. The measurement is in good agreement with the prediction over the first 60cm but for the rest of the L_r-range significant differences (values even above 0.01E(0)) are observed. This is explained by an 1.510^-4 rms fractional error of the cell dimensions. At larger distances the prediction would better agree with the data if the Q of the modes used in the calculations were lowered from the assumed value of 6500 to about 4000. Measurements of the loaded Q, however, show no evidence for the smaller values.

The wake function of two or more successive structures can be added to a total wake if the length of the combined sections is still small compared to the betatron wavelength.

A systematic detuning of multiple sections is limited by manufacturing tolerances. For a randomly distributed frequency error with the rms width, the effective transverse error-wake can be estimated by

(M is the number of sections). Even for one section it is difficult to keep below the desired level with realistic manufacturing tolerances. Therefore systematic section-to-section detuning is not considered for the present LC projects.

A random detuning of the center frequencies by leads to the envelope

If the arguments of the exponential function are in the order of i or larger the effective envelope is . As all sections of a LINAC are randomly detuned the particle dynamics over many betatron wavelength is affected and an 'effective' value of M cannot trivially be determined.

The recoherence of the wakefield in purely detuned structures takes place on a time scale _r=L_r/c which is short compared to the fill time _fill and therefore short compared to the length of the bunch trains considered in most LC design studies. Only a weak additional damping in the order of Q_r=f_cr is needed to suppress the long range wake. For the SBLC structure an average Q value of 3000 is needed, the goal for the NLC damped and detuned structure (DDS) of 1000 even allows the cell and alignment tolerances to be relaxed.

For the concept 'weak damping with few dampers' a large variety of coupling geometries and structure-damper configurations have been investigated. Due to the existence of trapped modes, damping cells inside a section are needed. E.g. for the SBLC structure, dampers would be needed at at least three positions, so that one damper is in the trapping range of each mode. Unfortunately even a damping cell inside the trapping range can be completely ineffective. This is the case for damping cells with two fundamental-mode-waveguides per polarization plane which do not break the dipole symmetry. To overcome this, either more or more complex one-cell-dampers (with broken symmetry, more than two waveguides or waveguides with more than one propagating mode) are required. Another disadvantage of special damping cells is their interference with the detuning: 'weak damping with few cells' needs an optimal cell-waveguide coupling which drastically disturbs the detuned short range wake. This effect can be lowered by increasing the number of dampers and reducing their coupling strength. The extreme is 'weak damping with one damper per cell'.

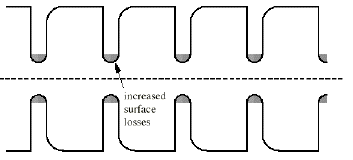
Usually the HOM-absorbers are separated from the accelerating mode by a special coupling geometry and/or frequency selective elements, but even with artificially increased losses at a part of the resonator surface, it is possible to achieve the needed selectivity [12]. Therefore the iris tips of all SBLC cells are covered by a material with ten to twenty times higher surface resistivity, as can be seen in fig. 2b. This decreases the quality of the accelerating mode by 5%, but the effective shunt impedance is lowered by less than 2.6%. As the iris coating is located exactly where the highest surface field strength occurs, investigations are necessary to prove the high power capability. The first tests with steel and Kanthal coated cells under conditions corresponding to an unloaded gradient of 25MV/m showed no evidence of surface break-down effects. Further measurements aiming to the doubled field in the 1TeV version are in preparation. To minimize the HOM excitation by active structure alignment, each section is equipped with two HOM pickups. One will be located near the front end, and one almost at the 2/3 point of the section length. The coupling to the circumference pickup waveguides is a compromise between the necessary resolution (about 10m) and the perturbation of the , k distribution.

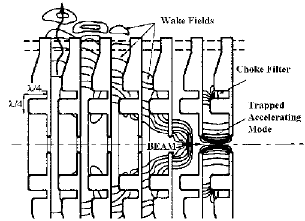
The damping of the NLC structure [13] is provided by a set of four waveguides that run parallel to the structure (see fig. 2c). In a localized sense the field in a tapered structure can be approximated as the superposition of forward and backward traveling waves. If their phase advance is close to that of the manifold waveguides, their energy can be drained to absorbers at the ends of the manifold waveguides. Additionally the excitation of all 'trapped' modes can be detected at these terminating loads. For each mode the coupling condition is fulfilled in the range of only few cells, therefore the damping can be controlled locally. The structure dimensions are determined in the following succession: the thickness and beam hole dimensions of the coupling irises are taken to be the same as those of the purely detuned section to retain their , k distribution. To reach the desired damping, the depth of the circumferential coupling holes and the widths of the waveguides are tapered. Finally the cavity radii are adjusted for the 2/3 accelerating mode. For the first 2/3 of the cells the depth of the manifold coupling holes is positive so that the shunt impedance degradation is less than 3%. In the last third the waveguides protrude into the cells which causes an increasing degradation to a maximum of about 5%.

Concepts for the suppression of long range wakes are presented for all multibunch LC design studies which take into account a large frequency range. With the exception of the SBLC iris coating, the NLC damped and detunded structure and the CLIC proposals, all techniques have been investigated in test structures. Besides refinements of the theoretical models and further test setups, economical manufacturing methods will have to be developed.

[1] R. Brinkmann et. al.: "TESLA/SBLC Conceptual Design Report", to be published 1996.

[2] G.Loew, T.Weiland (eds): "Linear Collider Technical Review Committee Report", 1995.

[3] M.Drevlak: "New Results on the Beam Dynamics in the SBLC". Internal DESY Report, M96-01, January 1996.

[4] T.Shintake, K.Kubo, H.Matsumoto, O. Takeda: "HOM-Free Linear Accelerating Structure for e+e- Linear Collider at C-Band", PAC95, May 1995.

[5] SLAC: Zeroth Order Design Report for the Next Linear Collider.

[6] M.Dehler, I.Wilson: private communication.

[7] K.A.Thompson et. al.: "Design and Simulation of Accelerating Structures for Future Linear Colliders", Particle Accelerators, Vol47, pp. 65-109, 1994.

Fig. 3. Damped structures: a) Concept of the HOM-free choke mode accelerating structure. b) Manifold damped structure. c) Damping by increased losses on the iris lip.

[8] A. Mosnier: private communication.

[9] K.Bane, R.Gluckstern: "The Transversal Wakefield of a Detuned X-Band Accelerator Structure", SLAC-PUB-5783. March 1992.

[10] J. Sekutowicz, 6th Workshop on RF Superconductivity, Newport News (1993).

[11] C.Adolphsen, K.Bane, H.Higo, R.Miller, R.Ruth, K.Thompson, J.Wang: "Measurements of Wakefield Supression in a Detuned X-Band Accelerator Structure", LINAC-94, Tsukuba, Japan, August 1994.

[12] M.Dohlus, H.Hartwig, N.Holtkamp, S.Ivanov, V.Kaljuzhny, A.Naboka: "Higher Order Mode Damping by Artificially Increased Surface Losses", DESY Report, to be published, 1996.

[13] K.Ko, K.Bane, R.Gluckstern, H.Hoag, N.Kroll, X.T.Lin, R.Ruth, K.Thompson, J.Wang: "Design Parameters for the Damped Detuned Accelerating Structure", SLAC-PUB-95-6844, May. 1995.