Rainer Wanzenberg
DESY, Notkestr. 85
22603 Hamburg, Germany
An important issue for a next generation e+e- high energy linear collider is the preservation of the beam quality through the acceleration in the linac. Recent design studies at different laboratories adopt very flat beams at the collision point to minimize beamstrahlung. Therefore most problems are related to the vertical single bunch dynamics which is determined by chromatic effects in the quadrupoles and wakefield effects in the accelerator structures due to the misalignment or vibrations of these linac components. Almost all linear collider designs consider multiple bunches in each rf pulse to raise the luminosity. The cumulative beam break-up instability due to long range wakefields (HOMs,higher order modes) is a severe problem for all multi-bunch schemes. Only the damping and detuning of the HOMs in the accelerator structures can reduce the long range wakefield effects. This report reviews several topics with respect to the preservation of the longitudinal and transverse beam quality in next generation linear collider designs. Single and multi bunch issues are covered.
Several linear collider designs are being considered to achieve e+e- collisions at a center-of-mass energy of 500 GeV with upgrade potentials to the TeV range. These collider studies include the following international collaborations: TESLA (coordinated by DESY), a linac using 1.3 GHz super-conducting cavities, the SBLC (also coordinated by DESY), based on S-band rf-technology, the JLC (coordinated by KEK), including 3 approaches with accelerating structures operated at S-, C- and X-band frequencies, the NLC (coordinated by SLAC), a X-band linac, VLEPP (coordinated by BINP), also using an rf-frequency in the X-band, and CLIC (coordinated by CERN), a two beam accelerator with 30 GHz rf-structures. An overview of these designs can be found in [1, 2].
Figure 1: Linear Collider, schematic overview.
A schematic layout of a linear collider complex is shown in Fig. 1. The actual layout of a linear collider differs from design to design. Some designs use a two stage bunch compression system, others use the spent e- beam for an undulator based e+ source, to mention only two possible differences to the shown schematic layout. The electrons and positrons are injected into damping rings to produce very small emittance beams, which are accelerated to 250 GeV in the main linac. The beam is delivered to the final focus system which focuse the bunches to a very tiny spot at the Interaction Point (optional two I.P.'s). The different linear collider designs are aiming at luminosities in the range of
with a vertical beam size of 
at
the (I.P.). To achieve this goal it is necessary not only to produce beams
with very small emittances of
but to preserve this emittance during the acceleration in the main linac.
The most critical plane is obviously the vertical. A comparison with the
1995 data from the SLC [3],
where the emittance dilution in the vertical plane is controllable to 
(initial
at 1.2 GeV),
demonstrates clearly the challenge of the design goals of a future linear
collider.
The increase of the transverse emittance of the beam is ultimately due to the misalignment or vibrations of the linac components, i.e. mainly the accelerator structures and the focusing magnets. When a bunch traverses an accelerator structures off-axis, wake field effects kick the tail of the bunch even more off-axis. Fig. 2 shows schematically how a bunch develops a banana shape while it is passing through several accelerator structures.
Furthermore, chromatic effects will affect the focusing of the bunches in the quadrupole magnets since the bunch is not monochromatic. Quantum excitation in the damping ring will produce an initial uncorrelated energy spread in the bunch. Additionally, a correlated energy spread of the bunch is induced by the rf-fields (acc. mode and wakes) in the accelerator structures.
Almost all existing linear collider designs, except VLEPP, consider the acceleration of a bunch train in one rf-pulse. The acceleration of multiple bunches has the advantage that the efficiency (AC power to beam power) of the linac is larger compared to a linac operated in a single bunch mode producing the same luminosity. Additionally, less synchrotron radiation is produced by beamstrahlung during the bunch collision, which improves the conditions for the high energy physics experiments with respect to the width of the luminosity spectrum and the backgrounds. Furthermore, the single bunch wake fields can be less severe since a lower single bunch charge can be used. Unfortunately, several complications are added due to transient beam loading and long-range transverse wake fields. The cumulative beam break-up instability, first investigated at SLAC [4], due to higher order dipole modes (HOMs) is a severe problem. These HOMs have to be damped and/or detuned to avoid this instability.
First consider the longitudinal dynamics of a single bunch. The bunch length is determined by the bunch compressors and is already frozen at injection into the main linac since the injection energy is at least 3 GeV. Longitudinal short-range wake fields will add to the initial uncorrelated energy spread a correlated one. Furthermore the slope of the rf-wave will influence the energy spread of the bunch, i.e. part of the wake-induced energy spread can be compensated if the bunch is properly placed off the rf crest. An energy spread will give rise to chromatic filamentation of betatron oscillations and dispersive effects in misaligned quadrupoles.
Fortunately, a correlated energy spread can be used to reduce the filamentation of the emittance when the bunch performs coherent betatron oscillations. This technique, called BNS damping [5], is based on the increased focusing of the low energy tail of the bunch. Since only the tail is driven off axis by transverse wakes, these effects will partly cancel. But randomly misaligned quadrupoles will still cause an increase of the emittance due to dispersion. Sophisticated orbit correction methods are needed to minimize these effects.
The bunch is focused by quadrupole magnets which are arranged in a FODO
lattice, characterized by the scaling of the beta function and the phase
advance with the energy. Almost all designs use a constant phase advance
of about 
and
a scaling of the beta function 
with
. The average
of the beta functions in the focusing quads (
) and in the defocusing quads ( 
)
is related to the FODO cell length Lcell and the quadrupole
strength K in the following way:
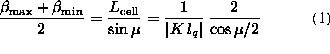
(lq is the length of the quadrupole). The choice for
the lattice parameters depends on the balancing of transverse wake field
and dispersive effects. The scaling constant a is mainly determined
by the BNS-damping condition. TESLA uses 
,
while most other designs use a=0.5. Actually the lattice is changed
in steps which follow approximately the scaling
law. Fig. 3
shows as an example the beta function of the SBLC design.
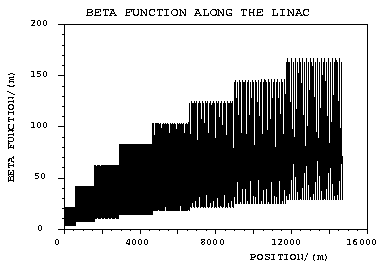
Figure 3: Scaling of the beta function along the linac. (Example:
SBLC, a=0.5).
Suppose that uncorrelated random kicks 
are
applied to the bunch along the linac. The rms orbit change at the end of
the linac (index f for final) is given by
The kicks at different positions n are transformed to an offset
at the end of the linac via the 
transport
matrix element. Adiabatic damping is included using the relativistic factor
. The kicks
give rise to an emittance dilution if different parts of the bunch are
affected differently.
This is indeed the case for dispersive effects. The kick depends
on 
and the
energy spread 
in
the bunch:
(The bunch goes through the quadrupole with an offset 
.)
The relative emittance growth due to dispersion depends on the energy spread,
the rms value 
,
acceleration gradient and average FODO cell length 
in
the following way:
The kicks due to transverse wake fields are given by:
where N is the single bunch population, 
the
length of one accelerator structure, 
the
offset of the bunch with respect to the axis of the structure and 
is
the transverse wake potential per length at the tail of the bunch (measured
in V/(C m2 ) ) depending on the longitudinal position s
in the bunch (see Fig. 2).
The transverse wake potential scales with the third power of the rf-frequency
of the accelerator
structure and with the square root of the bunch length 
.
Using the equations (2)
and (5)
the scaling law for the relative dilution of the normalized emittance is
obtained:
Using the parameters from references [1,
2]
the transverse wake field effects are compared in Fig. 4.
The right hand side of equation (6)
is calculated for each design and the results are normalized to values
obtained for the TESLA parameters. All designs but VLEPP are using multiple
bunches. The larger bunch population (VLEPP 
)
explains the difference between the NLC and the VLEPP designs, both using
a rf-frequency in the X-band.
To limit the emittance dilution to reasonable limits also for the high
rf-frequency linear collider designs it is necessary to align the accelerator
structures with higher precision. NLC accelerator structures have been
built with a 3 
m
precision. Furthermore, at SLAC S-band accelerator structures have been
aligned with a precision of 13 m
with respect to the beam using signals from higher order modes [6].
Furthermore one can gain from a stronger focusing and a higher gradient.
Additionally, it is 
,
i.e. the length of an accelerator structure lawill be
shorter and the emittance growth smaller:
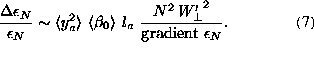
The filamentation of the bunch emittance due to betatron oscillations
can be significantly reduced by the BNS-damping technique, which was already
mentioned together with the correlated energy spread due to longitudinal
wakes and the slope of the rf-wave. Consider the orbit difference of the
head and the tail of the bunch 
.
The difference due to transverse wake fields is 
while
the effect due to dispersion is given by 
Both
effects cancel if the following BNS-damping / autophasing energy spread
is maintained during the passage of the bunch through the main linac:
with
The required BNS energy spread is constant along the main linac when the beta function is scaled with the square root of the energy. BNS-damping is not needed in the case of the TESLA design since the wakes are small due to the relative low rf-frequency of 1.3 GHz.
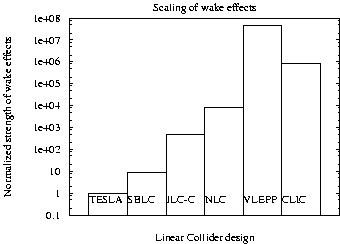
Figure 4: Comparison of the transverse wake fields effects for
the different linear collider designs.
The quadrupole magnets and the accelerator structures can be aligned
with a precision of about 100 m
rms by a careful survey. The length of the "ideal" reference
line is about a betatron wavelength at the end of the linac (say 500 m).
The beam position monitors (BPMs) can also be aligned with a precision
of better than 
m
rms with respect to the magnetic center of the quadrupole magnet. The usual
beam steering (one-to-one correction), which zeros the BPM readings, is
not sufficient to avoid a dispersive emittance dilution in a future linear
collider. The situation can be significantly improved by special orbit
correction techniques, often called beam based alignment. The basic
idea is to use difference orbit measurements in addition to the absolute
orbit measurements. The precision of difference orbits depend only on the
resolution of the BPMs, which is better than (say) 
m.
Especially the DF steering algorithm [7]
minimizes:
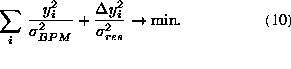
The orbit and difference orbit measurements enter into the equation with weight functions which are inversely proportional to their precision. The difference orbits are taken for different beam energies or equivalently with different quadrupole strength settings. Furthermore, different bunch charges can be used. The stability of the linac during the measurements has to be much better than the BPM resolution.
The acceleration of multiple bunches in one rf-pulse adds several complications to the beam dynamics. Strong transient beam loading will causes a bunch-to-bunch energy spread, which will amount to 20 % (SBLC, NLC, JLC) if not compensated. In a traveling wave accelerator section the first bunches of a train gain more energy than the later ones. The transient beam loading can be significantly reduced by the following methods:
Using these techniques the problem of bunch-to-bunch energy spread can be completely cured for the price of providing additional rf-power for the control.
Staggering the timing of the klystron pulses with respect to the bunch train is a non-local method to reduce the bunch-to-bunch energy spread. The other methods are more local ones based on a control of the amplitude or the phase of the rf. The drive power of the klystron can be used to ramp up the output rf-amplitude as the bunch train passes the accelerator section. This may have the disadvantage that the klystron is not always operated at saturation. An almost local method is achieved by a control of the rf-phases of two accelerator sections, which can be mutually in or out of phase with opposite sign. During the passage of the first bunches the two sections are out of phase and the transient beam loading is canceled. A SLED system is an rf-pulse compression technique which transforms a longer rf-pulse into a shorter one using a special cavity to store the first part of the rf-pulse. After a phase switch the second part of the rf-pulse is combined with the pulse from the cavity. The SLED pulse decreases during the beam pulse. The rate of the decrease can be adjusted to minimize the energy spread [8]. This SLED pulse shaping can be achieved by an rf amplitude modulation or a programmed phase variation.
Another very severe problem arising from a multiple bunch operation
is the cumulative beam break-up instability. The transverse long
range wake potential is the sum over several modes characterized by the
frequency 
,
the Q-value 
and
the transverse shunt impedance:
( 
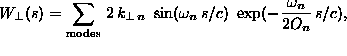
is
transverse wake amplitude of the n-th mode.) These modes are excited by
the bunches when the pass through the accelerator structure off-axis due
to misalignment of the structure or injection error. The excited fields
drive subsequent bunches of the train even more off axis leading to an
even stronger excitation of the modes in the next accelerator section (see
Fig. 5).
The bunch offsets from the axis grow exponentially: 
[9].
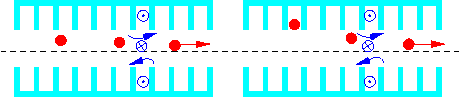
Figure 5: Cumulative beam break-up of a bunch train due to HOM's.
The instability can be suppressed by a special design of the accelerator structures. The cures are:
A detailed discussion of the subject can be found in [10].
The strongest damped structure is the choke-mode cavity, proposed for the
JLC-C design and already tested at S-band [11].
For the TESLA design a light damping of the HOMs to 
is
sufficient due to the large bunch spacing of 
s.
Mechanical motion of the quadrupole magnets due to ground motion can significantly degenerate the beam collision conditions in a linear collider. Diffusive ground motion processes can be described by the so-called ATL - rule:
the rms displacement 
of
two points separated by the distance l growth with 
.
A is nearly constant over a large frequency range. Measurements
for A are site dependent 
.
This type of random ground motion can also deteriorate the performance
of beam based alignment techniques. Systematic geological motion of the
bedrock, which can be dominant at some sites, is less important since the
effects can be corrected. Even quadrupole jitter can be reduced by feedback
systems.
Feedback systems are of general importance for linear colliders.
At the SLC the orbit and the energy of the beam are controlled by feedback
loops [12].
A feedback system can transform a tolerance on 
(say
a vertical position) into one on 
,
where 
is the
delay between two measurements. Due to this delay the feedback works only
for frequencies 
in the spectrum of the motion/jitter of y, if the sampling rate
is the repetition
rate of the linac. It is difficult to operate a feedback loop on the beam
even at frequencies greater than 
.
Generally one may distinguish orbit feedbacks which correct the average
orbit operated at a low sampling rate and fast orbit feedbacks using fast
kickers.
Fig. 6
shows the principle of a slow orbit feedback. The average bunch position
of the train is measured and corrected for the next pulse (or later pulses),
which can never be perfect due to the delay 
.
This is especially a problem if the repetition rate of the linac is low.
Therefore another variant of feedback loop is needed for the TESLA design
( 
Hz). Fig.
7
shows the principle. The offset of the first bunch is measured and the
offsets of the trailing bunches in the same pulse are corrected
by a fast kicker. The effective repetition rate for the TESLA design will
be 1.4 MHz. The bunch-to-bunch offset fluctuations due to long range wake
fields are small for the TESLA design.
Different from the feedback shown in Fig. 7 would be a feedback loop which samples from pulse to pulse but affects individual bunches. A multi-bunch pattern which is stable from pulse to pulse could be corrected by a very fast kicker.
Quadrupole jitter causes beam position jitter at the I.P. and degenerates the luminosity. Mechanical quadrupole motion can be measured by a geophone and corrected by a mover on the quadrupole support. A feedback system running with a sampling rate of 2 kHz has been successfully tested at DESY [13]. It was possible to stabilize the quadrupole motion to about 20 nm.
The contribution of resistive wall wakes to the wake field effects
is usually small. Nevertheless, these wake fields are important for very
short bunches ( 
m), which are
considered for Free-Electron-Laser facilities with very small tolerances
for the energy spread. Furthermore, resistive wall effects have to be taken
into account for collimators with small apertures.
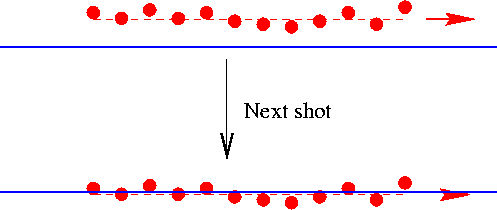
Figure 6: Schematic presentation of an orbit feedback system.
Thanks go to the colleagues from many laboratories which have provided the information for this paper. The presented material reflects their ideas and results.
