R. Assmann and F. Zimmermann
Stanford Linear Accelerator Center, Stanford University, Stanford, California
94309
Pulse-to-pulse variation of the transverse beam orbit, frequently referred to as `jitter', has long been a major problem in SLC operation. It impairs the SLC luminosity both by reducing the average beam overlap at the IP and by hampering precision tuning of the final focus. The origin of the fast orbit variation is not fully understood. Measurements during the 1994/95 SLC run showed that it is random from pulse to pulse, increases strongly with current and grows steadily along the SLAC linac, with a typical final rms amplitude of about half the beam size. In this paper, we investigate possible sources of the vertical orbit jitter.
In the Stanford Linear Collider (SLC), electron and positron
beams, which are extracted from two damping rings,
are accelerated in the 3 km long SLAC linac to about 50 GeV,
then separated and transported through 1.2 km long arc sections,
before they are collided at the interaction point
(IP). It is a long-standing problem of SLC operation, that
the vertical IP orbit position of
either beam varies markedly from pulse to pulse, by about
0.4- 
. The orbit
`jitter' at the IP is highly correlated to
the orbit variation measured at the end of the SLAC linac
and of about the same size. The jitter at injection into the linac is much smaller ( 
) and only poorly correlated to the IP orbit. The orbit variation has been a main
concern and the subject of intense studies during the 1994/95 SLC run
[1, 2, 3], in which the orbit jitter was observed to be random from pulse to
pulse and to grow steadily along the linac [1]. The jitter also appeared to be strongly
current-dependent (see Fig. 2).
The orbit jitter is a concern primarily for three reasons: first, it reduces the overlap of the two colliding beams at the IP and, thus, decreases the luminosity, by about 10%; second and more importantly, it makes measurements of the beam size with beam-beam deflections or wire scans more difficult. Sophisticated techniques using orbit information from strategical sets of upstream beam-position monitors had to be developed [4] to correct for the orbit jitter during a scan; third, as long as its origin has not been uncovered, the jitter adds an uncertainty to the design of future linear colliders.
In this report, we evaluate and compare the importance of
several possible jitter sources in the linac, namely: ground motion, uncorrelated quadrupole
vibration, accelerator-structure vibration, quadrupole field ripple, bunch length variation
and bunch intensity fluctuation. Throughout the text we specify the jitter as a percentage of the
beam size, assuming a normalized vertical emittance of 
m-rad at the end of
the linac.
The response of the linac to a harmonic vertical displacement of quadrupoles at a certain wavelength can be characterized by a lattice response function G, which is defined as the average squared ratio of the final orbit variation and the perturbation amplitude. For low current, wakefields are not important and G can be written as [5]
where 
denotes the wavenumber, 
is the position of the
jth quadrupole, 
is equal to 
for 
and 
equals 
; 
and 
are the (3,4) and (3,3)
transport-matrix coefficients, respectively, from quadrupole j or from the entrance to the end
of the linac; 
is the integrated strength of quadrupole j; 
and
denote the initial and final beam energy, and 
the energy at position
j, all three in units of the rest mass. We assumed that the vertical betatron-phase
advance across the linac is a multiple of 
, but this is not essential.
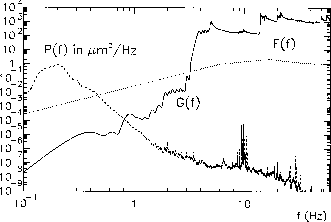
Using the dispersion relation between ground-motion wavelength and frequency that was measured in the SLAC linac tunnel [6], it is possible to convert the response function G(k), Eq. (1), into frequency space. The function G(f) thus obtained is represented by the solid line in Fig. 1, which shows that, at low frequencies, or large wavelengths, the response is strongly suppressed. Also displayed in the figure is the measured ground-motion power spectrum P(f). The spikes of P(f) around 10 Hz and 30 Hz are caused by vibration resonances of the accelerator supports. As a third (dotted) curve, the measured orbit-feedback response for the SLAC linac [7], F(f), is also depicted.
The integral over the product of P(f), G(f) and F(f) yields the rms orbit jitter caused by the ground motion [5],
assuming that all quadrupoles move
exactly as the ground beneath them. Integration over the frequency range from 0.008 to 64 Hz
predicts an rms orbit variation of about 40 nm with feedback on, and 32 nm without feedback. (The
main contribution to the integral (2) comes from the resonance-spikes at frequencies
where the feedback amplifies.) The nominal beam size for our reference point at the end of the
linac is 
m ( 
m, 
m
rad); hence, the expected jitter arising from ground motion is less than 0.001
.
At high current, dipole wakefields increase the effective 
matrix
elements by up to a factor of 3 [8]. Even with this additional factor of 3, the expected
jitter is still negligible.
Quadrupole vibration in the SLAC linac [9, 10] was measured to be of the order of 250 nm rms. Mechanical resonances in the quadrupole support structures, at 8-14 Hz and 28-30 Hz, as well as excitation by the accelerator-structure cooling water, at frequencies around 59 Hz, have been identified as its main sources [9].
If we assume that the quadrupole vibration is random and
uncorrelated, we can use the high-frequency limit of the response function G(f) in Fig.\
1 to estimate the resulting orbit jitter. Thus, we expect the orbit variation due to 250
nm rms quadrupole vibration to be amplified by a factor 
to a value of about 8 m or 
. Again, at high current, the beam response is
further increased by wakefield effects.
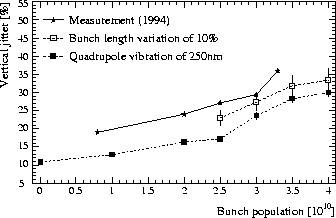
To confirm these rough estimates, we have performed a
computer simulation using the program LIAR [11]. The simulation includes the transverse
and longitudinal wakefields in the accelerator structures as well as the energy profile due to
BNS damping, i.e., the correlated energy spread introduced for wakefield
compensation. Specifically, the rf phase with respect to the rf crest in the first third (last
two thirds) of the linac is chosen as 22 
(-16.5 ) for bunch populations larger
than 
, and as 12 (-3 ) for 
. There is
no BNS phase change for the zero-current case. Simulation results are shown in
Fig. 2. The simulated beam jitter grows from zero at the beginning of the linac to the
final value shown. It increases linearly with the rms vibration amplitude.
The simulation confirms that quadrupole vibration can explain a substantial part of the observed SLC beam jitter.
The 12-m long girders which support the accelerator structures vibrate at rms amplitudes 
of about 1 m [9, 10]. Because an off-center beam induces a transverse
wakefield, also structure vibration can cause an orbit variation. For a driving point charge
transversely offset by y, the linear slope of the dipole wakefield is given
by [12] 
, where a denotes the
disk iris radius (a=1.16 cm). A Gaussian bunch of rms length 
experiences a
centroid kick of 
. Here, N
is the number of particles in the bunch. A kick 
received at position s causes an
orbit change 
at the end of the linac, where we have averaged over the betatron phase, 
is the beam energy at position s and the final beam energy, both in units of
the rest mass, and 
m denotes the average beta function.
The SLAC
linac consists of about 200 girders. Each girder carries four 80-cell structures. Let us assume
that the 4 structures on each girder and all cells which compound these structures vibrate at
about the same amplitude and in phase, and ignore possible correlations between different
girders. Abbreviating the number of cells per girder by 
, the number of girders by
, the final beam energy by 
, and averaging over the linac, one
finds
or 
. For a vibration amplitude of 1 m, a bunch length of
1 mm and 
, we obtain 
nm (0.008
), which is insignificant. In order to contribute sensibly to the observed orbit
jitter, the vibration amplitudes must be a factor of 5 larger (5 m rms); this seems rather
unlikely.
Quadrupole field ripple induces an orbit jitter of about
where 
and 
denote the rms beam offset and
ripple, respectively. We have used the relation [5] 
( 
is the strength of the ith quadrupole), which
can be derived by considering a constant vertical displacement of the entire beam line. Assuming
an rms orbit offset of 0.5 mm and using 
, we find that an
unrealistically large field ripple 
of 10% is required to explain an
orbit jitter of 0.5 .
There is some evidence that the longitudinal `sawtooth' instability which occurs at high current in the two SLC damping rings [13] contributes a sizable part of the jitter [14, 15]. Streak-camera and rf-monitor measurements show a pulse-to-pulse bunch-length variation of about 10%, both in the damping rings and in the linac [15, 14].
To study how a bunch-length change affects the orbit in the presence of
wakefields and with proper klystron phasing for BNS damping, we have again performed simulations
with LIAR [11]. We assumed realistic misalignments and correction methods, and included
orbit bumps for emittance control. A number of different random seeds were considered for the
misalignments. The simulation results, depicted in Fig. 2, suggest that a
bunch-length variation of 10% causes a beam jitter of 0.35 . Figure 3
displays the simulated vertical beam jitter as a function of position.
. The oscillations reflect a beta mismatch between the simulation and the design
lattice.
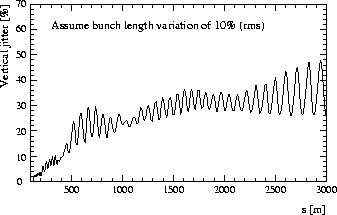
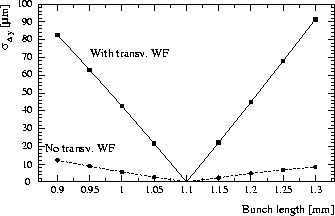
Figure 4 demonstrates that the orbit changes observed when
varying the bunch length are mainly effected by the transverse wakefields. These introduce a
dependence of the betatron phase advance on the bunch length, 
,
where 
denotes the girder length, and, thereby, convert bunch-length changes into
orbit jitter. In the SLAC linac, the effect of a betatron phase shift is aggravated by the large
orbit bumps over a few hundred meters, which are introduced for emittance reduction. Phase
advance variations result in an imperfect termination of these bumps, so that part of the
induced oscillation leaks out and manifests itself as jitter downstream.
Finally, we have
investigated the beam jitter due to current variation. According to our simulations, even for an
intensity variation as large as 5% the beam jitter is smaller than 0.04 , and, thus,
intensity changes do not appear to be important.
m rms trajectory oscillation in the SLAC linac. The solid line presents the full
simulation, while transverse wakefields were switched off for the dashed
curve.We have studied several possible sources of the vertical-orbit jitter in the SLAC linac. The most prominent source that we identified is the bunch-length variation of about 10%. Quadrupole vibration, with measured rms amplitudes of 250 nm, may account for much of the rest. Both these sources would lead to a monotonic jitter growth along the linac, consistent with observation. The effects of field-ripple, ground motion, structure vibration and intensity jitter all appear to be insignificant. We thank C. Adolphsen, F.J. Decker and T.\ Raubenheimer for helpful discussions.
