R. Assmann, C. Adolphsen, K. Bane, T.O. Raubenheimer, K. Thompson
Stanford Linear Accelerator Center, Stanford, CA 94309, USA
The main linacs of the next generation of linear colliders need to accelerate the particle beams to energies of up to 750 GeV while maintaining very small emittances. This paper describes the main mechanisms of static emittance growth in the main linacs of the Next Linear Collider (NLC). We present detailed simulations of the trajectory and emittance control algorithms that are foreseen for the NLC. We show that the emittance growth in the main linacs can be corrected down to about 110%. That number is significantly better than required for the NLC design luminosity.
Emittance preservation in the main linacs of a future linear collider like the NLC is demanding [1]. Strong wakefields and small emittances make the beams very sensitive to beamline imperfections. The achievable final beam emittance and luminosity depend strongly on the ability to avoid and to correct imperfections, especially quadrupole and Rf structure misalignments. Initial alignment errors are limited by the available accuracy of mechanical survey and alignment methods and are much larger than the required tolerances. Instead, beam-based alignment will reduce the initial errors to a level that meets the linac tolerances. This is a crucial step in the operation of a next linear collider and it must be verified that the procedure is understood and that the necessary precision can indeed be achieved.
We describe numerical calculations with the computer program LIAR [2] that were performed to study the NLC main linacs emittance transport. By assuming realistic errors in all major accelerator components, we can study the complex interactions between different mechanisms of emittance growth and the proposed correction algorithms.
The simulations were done for the 500 GeV version of NLC-II as defined in [1].
The beam consists of 90 bunches with 
particles per bunch. A bunch is 150 
m long and has an
initial uncorrelated energy spread of 1.5% at an injection energy of 10 GeV. The initial horizontal and vertical beam
emittances are 
m-rad and 
m-rad. We
assume that the chicanes in the diagnostics stations are switched off and that multibunch beam loading is perfectly
compensated. Finally, BNS damping as described in [1] is included.
The emittance growth in the NLC linacs is driven by transverse offsets between the beam and the centers of quadrupoles and structures. These offsets must be minimized in order to maintain the normalized emittances. We studied an algorithm that minimizes the quadrupole and structure BPM readings by first moving the quadrupoles, thereby steering the trajectory, and then moving the accelerator structures to align them along the beam trajectory. Because of imperfections in the accelerator model, a long linac is typically divided into many shorter regions of 50 to 100 quadrupoles and the algorithm is applied to each region individually. To obtain full correction, one usually has to iterate the correction multiple times. The simulations include the effect of finite BPM resolution (reading-to-reading jitter) and accelerator component misalignments.
The algorithm determines the quadrupole movements in an attempt to align the magnets in a straight line between the first and last quadrupoles of the region being considered; the first and last quadrupoles of the region are not moved by the algorithm. The beam is then launched along the beamline by adjusting either the initial conditions, for the first region of the linac, or by adjusting a single dipole corrector located at the first quadrupole for all subsequent regions; only a single dipole corrector is needed to join regions because the beam trajectory should be centered at the first quadrupole which is the last quadrupole of the preceeding region. Finally, weights can be added for the bpm resolution and the quadrupole movements; the nominal values are the expected bpm resolution and the expected quadrupole misalignments with respect to adjacent magnets. These weights will limit the magnitude of the moves, constraining the trajectory to lie along the pre-determined axis which can be assumed to be set by the initial mechanical alignment.
In specific, the quadrupole alignment algorithm finds the least squares solution to the problem:
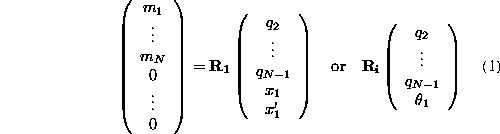
with a weighting vector given by
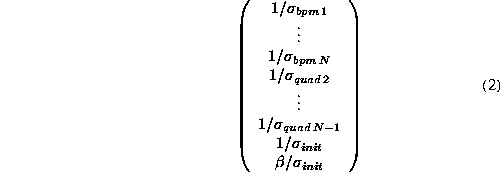
The measurement
vector consists of N BPM measurements 
followed by N zeros which are used to limit the quadrupole movements.
The solution vector consists of N-2 quadrupole movements followed by 
and 
which are the
initial conditions or 
which is a corrector located at the first quadrupole of the region. Next, the
weighting vector consists of 
, 
, and 
which are the estimated bpm
resolution, quadrupole misalignments and initial error which nominally would be equal to the quadrupole
misalignments. Finally, the matrix 
is given by:
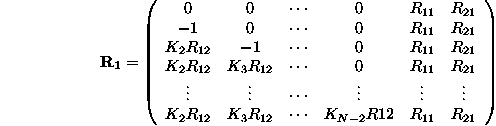(3)
where 
is the integrated quadrupole strength, 
is the (1,2)
transport matrix element from the 
quadrupole to the BPM, 
and 
are the (1,1) and (2,1)
matrix elements from the initial point to the BPMs.
After applying the quadrupole solution, the movers on the accelerator structures are adjusted such that the average RF-BPM reading on a girder is minimized. An RF girder supports two accelerator structures which each has two RF-BPM's at either end [3]. The RF-structure alignment is performed after each iteration of quadrupole beam-based alignment.
We assume that the step resolution of the magnet
and girder movers is infinitely small. The typical step size of 0.25 m is indeed small compared to the accuracy
of the RF-BPM's of about 15 m rms and can therefore be neglected for the RF-structures. The step size problem is
avoided for quadrupoles by having dipole correctors at each quadrupole that shift its effective magnetic center. Small
quadrupole misalignments are therefore corrected with dipole correctors. If the dipole strengths get large enough
they are `exchanged' into a step of the quadrupole mover.
We first consider a simple
case where we start with a random quadrupole misalignment of 100 m rms. Both types of BPM's are perfectly aligned
to the quadrupole and structure centers and have zero resolution. The quadrupole alignment is done in 14 regions
to allow for good convergence. Each region contains about 52 quadrupoles and is iterated 15 times. The number of
iterations is chosen higher than necessary in order to explore the optimal solution. The simulated misalignment of
quadrupoles, BPM's and RF structures, after the application of the interleaved alignment procedure, is shown in the
upper part of Figure 1. The dipole kicks at the bounderies between correction regions are shown
in the lower part of the same figure.
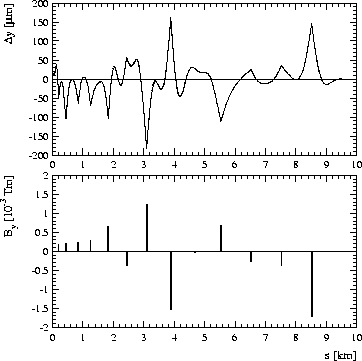
Figure 1: Example of the beam-based alignment algorithm with perfect BPM's and RF-BPM's. The initial random quadrupole
misalignment was 100 m rms. The alignment is done in 14 sections and 15 iterations. At the end of each section a
dipole corrector is used to launch the beam into the next section. The upper plot shows the misalignment 
of
quadrupoles, RF-structures and BPM's after alignment. The lower plot shows the integrated fields of the dipole
correctors.
A very smooth alignment between the endpoints of each section is
indeed achieved. At the endpoints the beam is deflected into the next section, causing sharp kinks. The endpoints are
not moved and reflect the initial random quadrupole misalignment of 100 m. Between the endpoints, the alignment is
bowed towards zero. This absolute zero line is known to the system only because the initial misalignment was random
about it. Constraints on the rms size of magnet movements bias the solution towards the initial average misalignment
between endpoints.
The solution shown in Figure 1 is largely determined by the choice of
, and . Changes in the relative weights will result in solutions that are
not equivilant in terms of emittance growth. We have chosen to constrain the rms magnet movements and the rms of the BPM
readings relatively strongly while allowing for large dipole kicks.
For a complete simulation run, we put the most
important imperfections together, apply the correction algorithms and observe the emittance growth. In order to
illustrate the importance of the several effects, we proceed in steps. For each case we quote the emittance
growth 
at the end of the linac and the rms beam offset 
at the
BPM's.
m rms. RF structures are aligned to
the beam.
m rms. Static BPM-to-quadrupole offsets of 2 m rms.
m rms.
rms. RF amplitude errors of 0.2% rms. Quadrupole roll errors
of 300 rad rms. Quadrupole gradient errors of 0.3% rms.
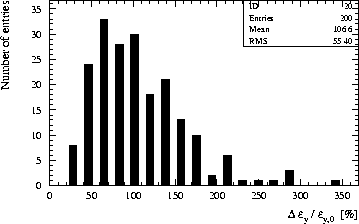
The most important imperfections are BPM and RF-BPM errors. They determine the quality of the correction and the residual emittance growth. In all cases, the correction and alignment is done on the first bunch, assuming that all other bunches behave similarly. The small additional multibunch emittance growth shows that this is a valid assumption, although we have not yet fully included the effects of internal structure misalignments. The distribution of emittance growth for different error distributions is shown in Figure 2 for the full simulation (last case). The exponential tail for large emittance dilutions tends to bias the average emittance growth towards larger values. It results from error distributions that have a large component at the betatron frequency. Fortunately, these errors are easily corrected using bump (global) correction methods.
for 200 different error distributions.
The average emittance growth is 106.6% 
3.9%. Note the exponential distribution for large emittance
dilutions.
A beam-based alignment algorithm for
quadrupoles and RF-structures was simulated with a realistic BNS configuration. It was shown that the large initial
misalignments from conventional alignment procedures can be corrected to acceptable levels. The emittance growth that
finally can be achieved depends on the initial misalignment and most importantly on the performance of the BPM's and
RF-BPM's. Assuming realistic imperfections in many subsystems we find a multibunch emittance growth of
106.6% 3.9%. This emittance growth is smaller than the allowed total emittance growth of 175% for the NLCIIb
parameter set. As the emittances roughly add in quadrature the impact of additional imperfections gets smaller with
larger emittances. It is anticipated that the alignment algorithm can be further optimized by smoothing the transitions
between alignment sections.
Future simulation studies will include internal structure misalignments, multibunch imperfections (bunch-to-bunch charge, energy, etc. variations) and the effects of missing BPM's. In addition, we further want to apply emittance bumps in order to compensate the emittance growth below what has already been achieved. Finally, we need to study the impact of different bunch shapes on the linac emittance transport.
* Work supported by the Department of Energy, contract DE-AC03-76SF00515