R. Assmann, C. Adolphsen, K. Bane, T.O. Raubenheimer, R. Siemann,
K. Thompson
Stanford Linear Accelerator Center, Stanford, CA 94309, USA
Linear accelerators are the central components of the proposed next generation of linear colliders. They need to provide acceleration of up to 750 GeV per beam while maintaining very small normalized emittances. Standard simulation programs, mainly developed for storage rings, do not meet the specific requirements for high energy linear accelerators. We present a new program LIAR ("LInear Accelerator Research code") that includes wakefield effects, a 4D coupled beam description, specific optimization algorithms and other advanced features. Its modular structure allows to use and to extend it easily for different purposes. We present examples of simulations for SLC and NLC.
The computer program LIAR is a numerical simulation and tracking program for linear colliders. The LIAR project was started at SLAC in August 1995 in order to provide a computing and simulation tool that specifically adresses the needs of high energy linear colliders. LIAR is designed to be used for a variety of different linear accelerators. It has been applied for and checked against the existing Stanford Linear Collider (SLC) as well as the linacs of the proposed Next Linear Collider (NLC). It is anticipated that LIAR will be applied to a broad range of problems for the various linear colliders that are studied at this time. Interested accelerator physicists from all laboratories are invited to join the LIAR project and both to use the program and to contribute new features. In this paper we point out some concepts and highlights of the program. A complete description is found in [1]. The physics concepts are described there in detail.
The LIAR code is mainly written in standard FORTRAN 77. It, however,
takes advantage of the STRUCTURE and RECORD extensions
that are available in most FORTRAN compilers. The code is stand-alone
apart from a few system calls (random number generator, time)
that might need to be adjusted to the actual computer system. No
specific libraries are required for the compilation. The present
LIAR version 1.4 is compiled and run under AIX 3.2 on IBM workstations.
Porting to other UNIX platforms is a straight forward process, as long as
FORTRAN compilers are available that support the STRUCTURE and
RECORD extensions. Porting to non-UNIX platforms might require
minor changes to the file handling. The computer should be powerful
enough to handle large blocks of memory (![]() 64 MByte).
64 MByte).
The internal data structures are designed in such a way that easy data access is guaranteed. An INCLUDE statement like
INCLUDE 'lattice.inc'will give access to all beamline information, including names, s-locations, magnetic fields, Rf phases, gradients, misalignments, Twiss parameters, beam offsets, emittances and many more quantities.
Let's consider an easy example. The beamline is defined in a structure ELEMENT that has pointers to the BPM structure. The following loop would print the vertical emittance at the BPM's for the whole beam and the first bunch:
DO I = 1, NUM.ELEMENT
IF (ELEMENT(i).IS_BPM) THEN
ibpm = ELEMENT(i).POINTER
WRITE(outlun,*)
1 BPM(ibpm).YEMITALL,
2 BPM(ibpm).YEMIT(1)
ENDIF
END DO
The emittance information at the BPM's is updated automatically
during each tracking. Another hypothetical example is to misalign all
quadrupoles vertically by 1% of the vertical beta function:
DO I = 1, NUM.ELEMENT
IF (ELEMENT(i).IS_QUAD) THEN
iquad = ELEMENT(i).POINTER
QUAD(iquad).DY =
1 0.01 * TWISS(i).BETAY
ENDIF
END DO
During the next tracking the new quadrupole misalignments will
be used. Those examples illustrate how easy it is to access and
manipulate the internal beamline information without a detailed
understanding of other parts of the program. Complete reference
information about the internal data structure can be found
in [1].
The goal to make LIAR easily extendable required a modular structure of the different parts of the program. It should be possible to add subroutines (commands in the LIAR language) without major modification to other parts of the program. Subroutine parameters are therefore passed through a command language. The main program knows only the name of a subroutine and passes the control with whatever parameters have been defined. It is the task of the subroutine to process and use the parameters properly. When the LIAR program is started without command line parameters then it enters an interactive mode:
___ ___
||| |||
||| ___ ______ ____
||| ||| _|||||| _||||
||| ||| ||| || |||
|||____ ||| |||__||_ |||
||||||| ||| |||||||| ||| Version 1.4
_________________________________________
L I near A ccelerator R esearch code
S L A C 1996 --- Ralph Assmann
Karl Bane
Tor Raubenheimer
Kathy Thompson
LIAR>
and
commands can be entered. Alternatively LIAR can be run in
batch mode, reading its input from a file.
Let's consider the example of a simple SLC simulation. We go through
it in steps, explaining the purpose of every part.
For most commands many more parameters than shown are
available. However, if parameters are not specified explicitely,
then they are set to their default values. Command lines are
automatically continued if an input line is ended with a comma.
In the first two commands we initialize all internal data structures to zero, we switch off the debug level and we set the output unit to the standard output:
RESET, all
SET_CONTROL, debug = 0,
outlun = 6
Then we read the lattice from a transport input deck and define the injection
energy:
READ_TRNS, infile = 'input/slc.trns',
energy = 1.19
In the next step the Rf-phases for BNS damping are defined and
the lattice is rescaled accordingly. Note that two different Rf-phases
are specified along the linac with the switch at 800 m:
SET_RF, energy = 50.,
scale = .t.,
phase1 = 22.,
lswitch1 = 800.,
phase2 = -16.5
Next we calculate the Twiss parameters, specifying the initial
values:
CALC_TWISS, betax = 3.40,
betay = 3.08,
alphax = 0.156,
alphay = 0.066
After that we need to define the initial conditions for the beam
setup. We define an initial beam offset y, the injection
energy and energy spread, the normalized emittances and the
Twiss values:
SET_INITIAL, y = 200.d-6,
energy = 1.19,
espread = 0.014,
nemitx = 3.0d-5,
nemity = 0.3d-5,
betax = 3.40,
betay = 3.08,
alphax = 0.156d0,
alphay = 0.066d0
Everything is prepared now to set-up the beam. We specify the
bunch population, the bunch length, the number of bunches, the
number of slices per bunch, the number of mono-energetic
beam ellipses per slice and the bunch spacing:
SET_BEAM, current = 4.d10,
blength = 1100.d-6,
nb = 1,
ns = 20,
nm = 3,
bspace = 0.
Next we have to define the wakefields. They are read in from
design specific input files. We only define short-range
wakefields:
SET_SR_WF, file = 'input/srwf_slc.dat'Before we track the beam through the lattice, we misalign all quadrupoles vertically by 200 µm rms:
ERROR_GAUSS_QUAD, name = '*',
y_sigma = 200.e-6
Now we can finally track the beam through the lattice:
TRACKand measure the normalized beam offsets at the BPM's:
MEAS_BPM, file = 'output.data',
norm = .t.
The output is saved into a file. As already mentioned many
more parameters and commands are available in LIAR. For example
the command TRACKC would have tracked the beam through the lattice
while applying a 1-to-1 trajectory correction. The complete
reference information is available in the LIAR manual [1].
During the execution of the commands LIAR provides extensive information. For example the progress of the tracking is indicated by a "trackometer":
T R A C K O M E T E R : ~~~~~~~~~~~~~~~~~~~~~~~ 0 10 20 30 40 50 60 70 80 90 100 % |____|____|____|____|____|____|____|____|____|____| ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^At the end of the tracking, summary information is printed to the standard output:
End of tracking A N A L Y S I S :
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Beam energy
- acceleration: E_0 = 1.190 GeV --> E_f = 45.998 GeV
- spread: E_sig = .016 GeV --> E_sig = .126 GeV
- rel. spread SIGE/E = 1.322 % --> SIGE/E = .274 %
Beam blow-up
- Emittance (b1): g_x = 41.680 % g_y = 205.158 %
(av): g_x = 41.680 % g_y = 205.158 %
(train): g_x = 41.680 % g_y = 205.158 %
- Lumin. factor: R_x = 91.1 % R_y = 86.2 %
- BMAG mismatch: BMAGX = 1.016 BMAGY = 1.368
Initial beam size:
- Horizontal: S_x = 275.8 um S_x' = 65.2 urad
- Vertical: S_y = 87.5 um S_y' = 24.2 urad
Final beam size:
- Horizontal: S_x = 135.911 um S_x' = 3.856 urad
- Vertical: S_y = 50.695 um S_y' = 1.420 urad
Jitter offsets wrt reference 1 for bunch 0:
- Horizontal: J_x = .43 um J_x' = .67 urad
- Vertical: J_y = 10.48 um J_y' = .63 urad
Beam trajectory (ideal)
- average: X_av = 12.26 um Y_av = 16.96 um
- RMS: X_sig = 193.92 um Y_sig = 188.15 um
Beam trajectory (BPM readings)
- average: X_av = 16.79 um Y_av = 16.82 um
- RMS: X_sig = 192.62 um Y_sig = 224.57 um
Final beta functions
- from beam: B_x = 26.67 m B_y = 59.39 m
- from TWISS: B_x = 22.13 m B_y = 27.25 m
Final alpha functions
- from beam: A_x = .7744 A_y = -1.992
- from TWISS: A_x = .7051 A_y = -.700
Final geom. emittance
- initial value: E_x = 1.29E-08 rad*m E_y = 1.29E-09 rad*m
- wrt centroid: E_x = 4.72E-10 rad*m E_y = 1.02E-10 rad*m
- wrt axis: E_x = 2.42E-09 rad*m E_y = 3.66E-10 rad*m
Final norm. emittance
- initial value: E_x = 3.00E-05 rad*m E_y = 3.00E-06 rad*m
- wrt centroid: E_x = 4.25E-05 rad*m E_y = 9.15E-06 rad*m
- wrt axis: E_x = 2.18E-04 rad*m E_y = 3.30E-05 rad*m
The data from this summary output is explained in [1].
We just mention a few of the summary results: emittance growth in the
linac, lattice mismatch, Rms trajectory offsets, beam energy, ....
In addition most of the results are saved at every BPM location.
They can be printed out into files, for example in order to study
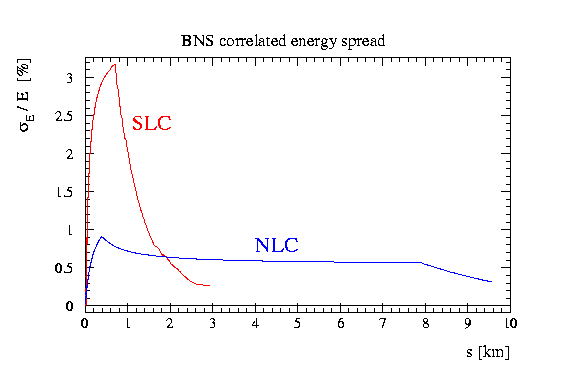
the emittance growth along the linac. An example is shown in
Fig. 1, where the beam energy spread is shown as a function
of longitudinal position s for both the SLC and the NLC. This example
demonstrates the advantage, if different linear colliders are simulated
with the same computer program. Results can be compared immediately,
allowing new insights in the underlying beam dynamics.
The application on SLC allows particularly to "calibrate" the simulation results against the experience in a real linear collider. LIAR results from SLC and NLC simulations are presented in [2, 3, 4].
The LIAR program is presently limited to linear accelerators without bending magnets. It is assumed that the longitudinal charge distribution remains unchanged. This is perfectly valid for linear accelerators. However, bunch compressors can not be simulated. For example, LIAR is now also used for the modelling and simulation of the SLAC Linac Coherent Light Source (LCLS) [5]. Bunch compressors are an important part of this proposal. Further we have not yet implemented sextupoles or any matching abilities into LIAR.
The correct treatment of bending magnets will be implemented into LIAR in the near future. This will allow to include bunch compressors into the simulation. We further plan to implement automized dispersion-free steering algorithms into the program. However, those are just two examples of future additions. There are many more useful extensions of LIAR. We invite all interested accelerator physicists to join the LIAR project and to contribute their experience and knowledge.
*Work supported by the Department of Energy, contract DE-AC03-76SF00515