A 40 MeV electron beam, using the inverse free-electron laser interaction, has been accelerated by E/E = 2.5 % over a distance of 0.47 m. The electrons interact with a 1-2 GW CO₂ laser beam bounded by a 2.8 mm ID sapphire circular waveguide in the presence of a tapered wiggler with Bmax 1 T and a period 2.89cm _w 3.14 cm. The experimental results of E/E as a function of electron energy E, peak magnetic field Bw and laser power W_l compare well with analytical and 1-D numerical simulations and permit scaling to higher laser power and electron energy.

The study of the Inverse-Free Electron-Laser (IFEL) as a potential mode of electron acceleration has been pursued at Brookhaven National Laboratory (BNL) for a number of years [1-4]. Recent studies have focused on the development of a low energy, high gradient, IFEL accelerator [5] as a first step toward a multi-module electron accelerator of maximum operating energy of a few GeV. Experimental verification of the IFEL accelerator concept was obtained in 1992 [6] , using a radiation wave length of = 1.65 mm, and more recently [7] using a wavelength of 10.6 m. In this report further experimental evidence of the IFEL interaction ( = 10.6 m) is presented. The experiment used a 50 MeV electron beam, a 1-5 GW CO₂ laser beam provided by BNL's Accelerator Test Facility (ATF) and a uniquely designed period length tapered wiggler.

The wiggler is a fast excitation electromagnet with stackable, geometrically and magnetically alternating substacks of Vanadium Permendur (VaP) ferromagnetic laminations, periodically interspersed with conductive (Cu), nonmagnetic laminations, which act as eddy current induced field reflectors [8,9]. Four current conducting rods, parallel to the wiggler axis, are connected at the ends of the assembly, constituting the excitation loop that drives the wiggler. The overall wiggler stack is easily assembled, is compressed by simple tie rods, and readily permits wiggler period (_w) variation. Configured as a constant period wiggler, _w = 3.75 cm and B_max = 1 T, the system has shown [10] an rms pole-to-pole field variation of approximately 0.2 %.

The CO₂ laser beam is brought into the IFEL interaction region by a low loss dielectric (Al₂O₃ ,sapphire) circular waveguide which evidenced very good transmission properties [11] of the high power CO₂ laser beam. Extensive studies were carried out to establish optimum coupling into the guide and to measure the transmission loss of the long (1.0 m) extruded single crystal sapphire guides. Also, because of the overmoded guide configuration (ID = 2.8 mm), attempts were made to determine the transverse mode spectrum. To this end various wave guide configurations were tested at low laser beam power with the beam focused to a Gaussian waist with adjustable radius at the entrance of the waveguide. The beam profile was measured using a pyroelectric vidicon TV camera combined with digital frame grabber. For the 2.8 mm. ID sapphire dielectric guide a laser power attenuation factor of 0.2 dB/m was measured. The laser beam profile within the guide was inferred by measuring the beam diameter at the guide exit for various guide lengths.The results show that, commensurate with the near constant beam profile within the guide, the mode structure is dominated by the guide fundamental mode only. This is in accord with the absence of mode mixing reported in Ref.[11] for filamentary sapphire guides for CO₂ laser radiation transport.

In the IFEL accelerator, the electron beam is accelerated by the interaction with the laser radiation wave in the medium of a periodic wiggler field. The theoretical description of the interaction has been given by a number of authors [3,12]. Approximate analytical expressions derived in Ref.[3] were used to parameterize a single acceleration stage. Subsequently, 1-D and 3-D simulation programs were written solving the self consistent system of Lorentz equations for the electrons and the wave equations for the input laser field as discussed in Ref. [12]. The 1-D program has been used to determine the self-consistent wiggler period length and its taper for given values of electron beam energy and laser power and to calculate the bucket acceptance and bucket leakage for a single or multi module accelerator. The 3-D code has been used to study beam walk-off, transverse phase space distributions and emittance growth.

Extensive IFEL simulation studies were carried out both for a single IFEL accelerator module and for a sequence of IFEL modules. The objective of the present experiment was a proof of principle performance of a single IFEL unit incorporated in beam line II of the ATF [13,14]. A schematic layout, specific to the IFEL experiment only, is shown in Fig.1. Beam transport downstream from the nominal 50 MeV Linac is so dimensioned as to yield a dispersion free IFEL interaction

region. The electron beam, at the IFEL location, is matched vertically to the natural wiggler betatron amplitude _y = 0.17 m, _x = 0.0 and to a horizontal amplitude _x = 0.3 m, _x = 0.0 . Downstream of the IFEL interaction region the optical system is configured as a momentum spectrometer with adjustable dispersion magnitude (0.0 < _p < 3.0 m) at a diagnostic endstation; there the beam momentum dispersion is measured by means of a phosphor screen-vidicon TV camera-Spiracon frame grabber. Also shown schematically in Fig.1 is the CO₂ laser beam entry into the interaction region vacuum envelope through a ZnSe window, and its propagation as a free-space mode, to the sapphire dielectric waveguide entry. With deliberation, the dielectric guide was taken to be 0.6 m in length, whereas the accelerator module length (wiggler length) was set at 0.47 m. This was done to approximate a mode matching section, enhancing thereby the mode purity in the IFEL module proper.

The design parameters used in this IFEL accelerator experiment are listed in Table 1. With optimized overlap of the electron and CO2 laser beams, both spatially and timewise, and the interleaving of the lower repetition rate CO₂ laser pulses with the higher repetition rate electron beam pulses, the IFEL electron beam acceleration could readily be established. 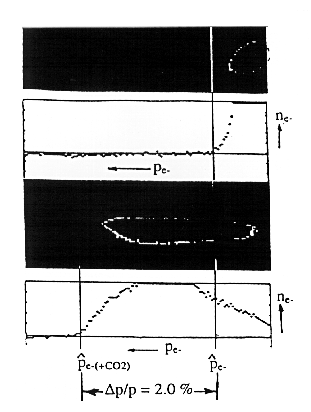Electron acceleration was measured with the spectrometer at the diagnostic screen. An example of the momentum spectrum of the unaccelerated and accelerated electrons is given Fig.2, where the beam intensity distribution is shown versus xx ⁺ pp/p, with the spectrometer optics adjusted so that pp/p >> xx . Optimization of the IFEL effect and exploration of parameter space,

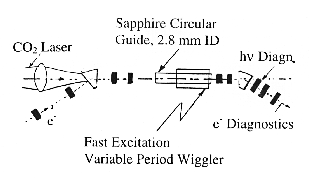
Table 1. IFEL Experiment, First Phase

e- beam	Injection Energy	40.0	MeV
	Exit Energy	42.3	MeV
	<Accel.Field>	4.9	MV/m
	Current, nominal	5	mA
	N(bunch)	109	e-
	I(max.)	30	A
	E/E(one )	3.10-3
	Emittance (one )	7 10.-8	m.rad
	Beam radius	0.3	mm
Wiggler	Wiggler Length	0.47	m
	Section Length	0.6	m
	Period Length, w	2.9--3.1	cm
	Wiggler Gap	4	mm
	Field max.	10	kG
	Beam oscill.,a1/2	0.16-0.2	mm
CO2 Laser	Power, Wl(Laser)	109	Watts
	Wave Length,	10.6	m
	Max.Field, Eo	0.78 103	MV/m
	Guide Loss,	0.05	m-1
	Field Attenuation	0.26	dB/Sect.
	Pulse, (fwhm)	220	psec
	Ao	1.53 103
	ro(Lw/2)	1.0	mm

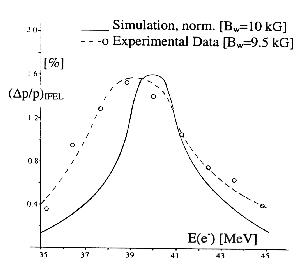
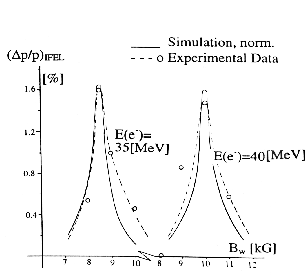
with variation of the electron beam injection energy, CO₂ laser power and wiggler maximum magnetic field magnitude was carried out in several consecutive runs, the results of which established the unambiguous signature of the IFEL acceleration. This is illustrated in Figs.3 and 4, where (E/E)_IFEL is shown both as given by the 1-D model simulations and as obtained experimentally. Fig.3 shows the relative energy gain for B_w and W_l constant; in Fig.4 the plot (E/E)_IFEL vs. B_w is given.

The approximate IFEL design equations [3] are:

d/dz = A(K/)f(K)sin with = (k + k_w)z - kct (1)

where the normalized laser electric field is A = (e/mc²)(1/R_o)(W_lZ_o)^1/2 , K = (eB_ww)/(2mc) 2.7 is the wiggler parameter, f(K) 0.38 is a correction factor due to the linear polarization of the wiggler, Z_o = 377 , R_o is the waveguide radius and k, k_w are the radiation and wiggler wavevectors, respectively. The resonance condition leads to:

= 0.5 _w/²(1 + K²/2) (2)

The relative energy gain of the electron beam in a wiggler of length L_w is:

/ = (p/p)_IFEL = A(K/²)f(K)sin_rL_w where (3)

_r is the resonance phase (45^o for optimum bucket size).

In Fig.3 the solid line shows the results of the numerical simulations with laser power W_l = 1 GW and B_w = 10 kG normalized to the maximum experimental value. The agreement of the simulations with the experimental results are good. Similarly, in Fig.4 experimental results are compared with the simulations for 35 MeV and 40 MeV, in both cases the agreement is good. The maximum (p/p)_IFEL for initial electron energy

of 35 MeV leads to a value of the magnetic field B_w = 8.35 kG, to be compared with the experimental value of 8.44 kG, and for E = 40 MeV, the calculated B_w is 9.98 kG and the experimental value was B_w = 9.96 kG.

In conclusion, the IFEL acceleration of a 40 MeV electron beam by E/E = 2.5 % with a 1 GW CO₂ laser and a tapered wiggler with peak field on axis of 10 kG has been confirmed. Agreement with the model predictions is satisfactory, permitting the scaling of anticipated results to

higher laser power. Present IFEL operation is limited to a maximum laser power of 2 GW. With the upgrading

of the ATF CO₂ laser to the 1TW level as presently underway, an IFEL mean acceleration gradient of 100 MeV/m might become achievable.

The authors wish to acknowledge the invaluable support and participation in the experiment of the ATF staff M. Babzien, K. Batchelor, I.Ben-Zvi, A.Fisher, K. Kusche, R. Malone, I.Pogorelsky, J. Qiu, T. Romano, J.Sheehan, J.Skaritka, T. Srinivasan-Rao and X-J Wang.

This work was supported by the Advanced Technology R&D Branch, Division of High Energy Physics, U.S.Department of Energy, DE-AC02-76CH00016.

[1] R. Palmer, J. Appl. Phys. 43, 3014 ,1972.

[2] C. Pellegrini, P. Sprangle,W. Zakowicz, Proc. of the XIIInt.Conf. on High Energy Accelerators, p.473 ,1983.

[3] E. Courant,C. Pellegrini,W. Zakowicz, PR A32, 2813,1985.

[4] A. Fisher, J. Gallardo, J. Sandweiss, A.van Steenbergen, "Inverse Free Electron Laser Accelerator", Proc. Adv. Accel. Concepts, Port Jefferson, NY, AIP 279, p.299 ,1993.

[5] A. Fisher, J. Gallardo, A. van Steenbergen, J. Sandweiss, "IFEL Accelerator Development", Nucl. Instr. Meth.A341,1994

[6] I. Wernick and T. C. Marshall, Phys. Rev. A46, 3566 ,1992.

[7]A.vanSteenbergen,J.Gallardo,J.Sandweiss,J.Fang,M.Babzien,

K.Batchelor,A.Fisher,K.Kusche,R.Malone,I.Pogorelsky,J.Qiu,

T.Romano, J.Sheehan, J.Skaritka, T.Srinivasan-Rao, XJWang, "Inverse Free Electron Laser Single Module e^- Acceleration",

Proceedings BNL CAP/ATF Users Meeting, Dec., 1995

[8]A.van Steenbergen,Pat.Appl.368618,June 1989 (Aug.'90)

[9] A. van Steenbergen, J. Gallardo, T. Romano, M. Woodle, "Fast Excitation Wiggler",Proc.PAC SF.,IEEE NS, May 1991

[10]A.Fisher,J.Gallardo,A.van Steenbergen,J.Sandweiss,J.Fang, "IFEL Development",VI Workshop Adv. Accel.,Fontana,WI '94

[11] J. Harrington, C. Gregory, Optics Letters 15, (1990)

[12] N.Kroll, P.Morton, M.Rosenbluth,Physics of QE 7,89,1979

[13] I. Ben-Zvi, Proc. Adv. Accel. Concepts, Port Jefferson, NY, AIP 279, 590 (1993)

[14] I. Pogorelsky, Proc. Adv. Accel. Concepts, Port Jefferson, NY, AIP 279 608 (1993)