For the development of accelerators the key problem is the maintenance of radial and phase stability of the flow. Wide opportunities in this direction are opened by the application of superconductive systems with using the effects of magnetic potential well.Without restricting the generality of the problem, as a particular case, we have considered the stability and stationary motion conditions for charged particles in the electromagnetic fields of ideally conductive rings. Results of theoretical analysis, based on Lyapunov's stability theory, of the radial and longitudinal particles motion in the superconductive magnetic system are presented. The estimation of criterion and conditions of beam stability is given.

It is generally recognized that simultanous attainment of the intense beam stability along all the coordinates is not possible without involving into interaction the external stabilizing magnetic fields. On our opinion the new principal method of approach to decision of the question of stabilization and concentration of the charged particle beams cosists in the development of superconducting (SC) control system based on the use of the effect of the magnetic potential well (MPW) [1].

As a particular case, let us study the possibility to use this effect for formation of the electron ring in the collective ion accelerator. Consider the dynamics and stability conditions for particles of the electron ring in the field of the SC magnetic contour (see Fig.1).

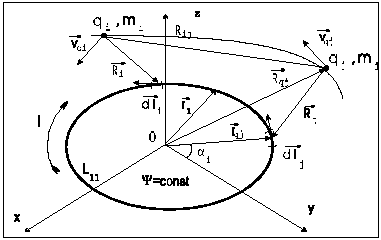
For the case of the movement of S-charge particles in the electromagnetic field of the ideally electroconductive ring the Lagrange function to members of the order has the form[2]:

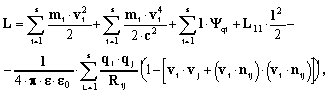
( 1 )

where ,, - mass, velocity and charge of the i-particle,- flow, created by i-charge through contour,

- current in SC ring,- distance between two charges, - physical constant, - normal vector in the direction between and charges.

The stationary movement on circular orbit imposes the necessary conditions of stability on the system:

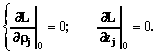(2)

The given conditions should be executed for any orbit. Assuming that the particles move slowly we receive the Lagrange function in the form:

(3)

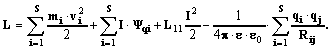
For analysis of the stationary movement we enter the dimensionless parameters of the system:

- the dimensionless radius of the j-particle orbit;

- the dimensionless angular coordinate of the

j-particle;

- the dimensionless deviation from the plane of

orbit at stationary movement;

; - radius is SC contour.

Expressions:

; ; ;

(4)

represent the speeds of the appropriate dimensionless coordinates., where has the dimension 1/c, and t represents the time coordinate.

We enter new parameters:

,

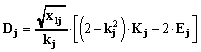
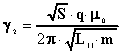,, (5)

where - is the magnetic flux frosted in the SC ring;

K, E - are the elliptic integrals of the first and second kinds of the modulus .

The new constant of the particle interaction (Coulomb) and the dimensionless constants and as well as the dimensionless current and speed of the particles determine the final version of equations.

These cyclic coordinates are connected with two first integrals of the motion which are the law of conservation of momentum and the law of conservation of magnetic flow:

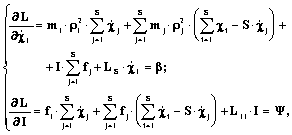(6)

or after correspoding transformations:

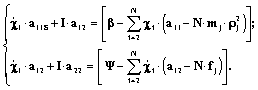(7)

- is the moment of momentum of system;

, .

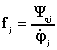
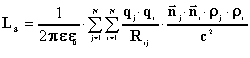
We transit from the Lagrange function to the Hamiltonian. The division is proceeded accurate to the second member expansion in theTaylor series concerning the position of the balance:

(8)

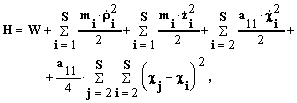
where .

It is clear, that the members not included in the W function are definitely positive accurate to the second in finitesimal order at expansion in the Taylor series in the vicinity of the equilibrium orbit.

We enter the designations:

,

, .

According with Lyapynov's stability theory, if we want to stabilize the system, we need to satisfy conditions:

, . (9)

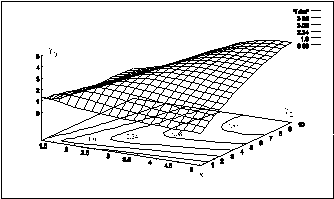
For considering case conditions (9) for the stationary orbit be existing are submitted on Fig.2.

Fig.2. Condition for the stationary orbit be existing.

Let perturb the system and consider the criteria of electron ring stability in the plane of the ideal conductive contour. Then it is possible to expance the W function in the Taylor series in the vicinity of origin of coordinates:

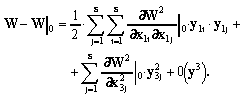(10)

Last expression represents the Lyapunov function for the system of charges and the ideal conductive ring. The linear members of the expansion vanish proceeding from the necessary conditions of the stability ( 9 ).

Here we have the Lapunov's function in the square-law form:

. (11)

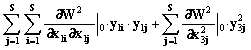
According with Silvestr's criterion, the real square-law form ( 11 ) will be definitely positive, if all main minor of its determinant are positive, than it is provided by the completion of the inequalities:

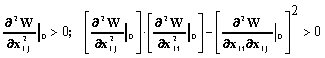
( 12 )

concerning to the radial stability;

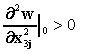(13)

concerning to the longitudinal stability.

The numerical experiments show, that the inequalities(12,13) are fulfilled in a wide range of magnetic and geometrical parameters of the system, that is seen from the results of numerical analysis submitted on Fig. 3,4,5.

=const, .

=const, .

Fig. 5. Space of stability as a function .

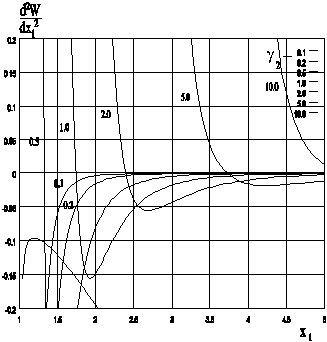
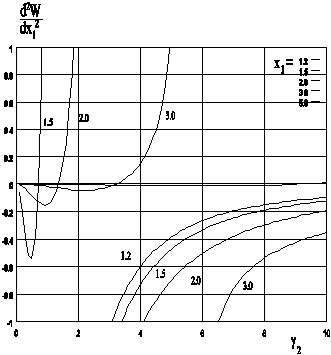
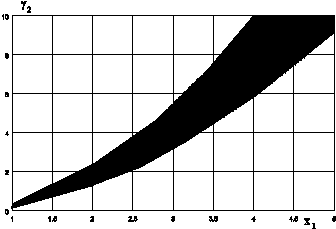
So, the above analysis shows that the system for formation and accompaniment of electron bunches of toroidal geometry with included SC elements guarantees the stable process run in the parameter range sufficient for the practical achievement.

[1] V.S.Mihalevich, V.V.Kozorez, V.M. Rashkovan and etc. "Magnetic potential well - effect of stabilization superconductive dynamic systems", Kiev, Naukova Dumka, 336 p (1991)

[2] A.M.Korsunsky,N.S.Repalov, Yu.D.Tur. "Control of the Parameters of Electromagnetic Field in the Linear Accelerators". Particle Accelerators ,vol. 11, p11(1980)