It is well known that coupling slots between adjacent cells in a -mode structure reduce shunt impedance per unit length with respect to single cell cavities. To design optimized coupling slots, one has to answer the following question: for a given coupling factor, what shape, dimension, position and number of slots lead to the lowest shunt impedance drop? A numerical study using the 3D code MAFIA has been carried out. The aim was to design the 352 MHz cavities for the high intensity proton accelerator of the TRISPAL project. The result is an unexpected set of four "petal" slots. Such slots should lead to a quasi-negligible drop in shunt impedance: about -1% on average, for particle velocity from 0.4 c to 0.8 c.

The TRISPAL[1] linac is designed for producing a 40 mA beam of 600 MeV protons. The aim is tritium production from spallation neutrons. The main part of the linac (from 100 to 600 MeV) is made of coupled cells cavities at 352 MHz. This rather low frequency has been chosen for klystron availability, and because SUPERFISH simulations showed that for a given beam tube diameter (= 50mm), the shunt impedance was almost the same for 352 and 704 MHz cavities. Moreover, this choice leads to a small number of cell per cavity which permits to use the simple and efficient -mode structure.

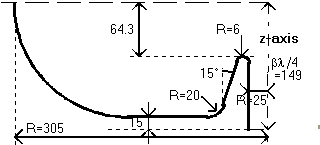
First of all, the 2D geometry has been optimized with the code SUPERFISH [2]. The resulting cell is shown in fig.1.

In a multi-cell cavity [3], slots have to be performed between adjacent cells in order to spread the RF power within the whole cavity. They must be big enough to insure a flat -mode, but usually, this reduces the shunt impedance.

A systematic optimization of the slots has been carried out with the code MAFIA. We chose a fixed velocity value (=0.7) and started with slots inspired from the LEP cavities [4]. We computed the coupling factor, defined from the frequency difference between 0 and modes:

, (1)

and the shunt impedance drop defined from the difference of shunt impedance between -mode and a single cell cavities:

, (2)

in which indices , 0 and 1 represent values of -mode, 0-mode and single-cell modes, respectively. As these differential values are rather small, the three cases are always computed with an identical mesh, in order to get rid of the bias due to the meshing approximation.

In order to distinguish between volume energy and surface dissipation effects, we split the shunt impedance into two factors; quality factor Q and geometrical impedance:

. (3)

Analogously to R, relative variations of Q and g (between -mode and single cell) are noted Q and g, respectively.

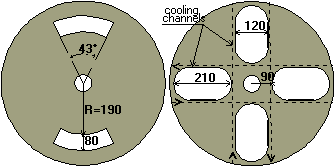
Then, we changed step by step the size, the number and the shape of the slots. At each step, we watched how the coupling factor and the shunt impedance drop would vary. Our goal was to keep the same coupling factor and to minimize the shunt impedance drop. We will not give here the winding path we followed during the optimization process, but fig. 2 shows the starting and ending points. Fig. 3 is a 3D view of the MAFIA computation.

We will consider here variations from the 4-petals geometry to show that it is optimized. All the results about Q, g or R are given with respect to a single cell cavity.

Number of slots. First of all, the number of slots per disk has been reduced to two instead of four.

Roughly, all effects are proportional to the number of slots. The "price" for coupling is approximately : R 0.7 .

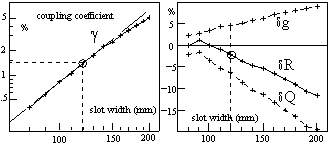
Slot width. It has been varied from 80 to 200 mm. As shown in fig. 4, the coupling coefficient is approximately proportional to the cube of the slot width. On the other hand, the shunt impedance drop increases linearly from a slot width of 100 mm. From this value, the price to pay for increasing the coupling is: d(R)/d 3. This is much more "expensive" than increasing the number of slots. This would suggest a slot width of 100 mm with six slots per disk. But, compared to the optimized solution, the shunt impedance improvement would be rather small and the cooling circuit would be much more complicated.

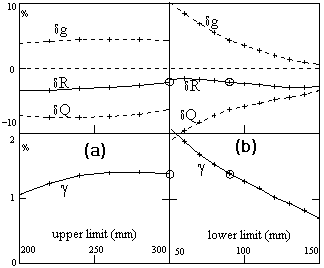
Slot height. Upper and lower limits measured from the axis have been varied independently. Fig. 5a shows that the lowest shunt impedance drop is reached by the highest upper limit, while the coupling coefficient remains constant in this area. We just kept a 5 mm margin from the highest possible value of the upper limit (i.e. the cell radius), in a way to simplify the mechanical design. Fig. 5b shows that the lower limit should be as small as possible: the coupling increases and the shunt impedance drop gets smaller. The limitation is given by the cooling circuit.

As proton energy varies along the linac, the cell length varies according to the velocity, and the gap length has to be adjusted. Simulations showed that the goal frequency could be reached by varying the gap length according to:

gap = 234 mm ( - 0.15 ).

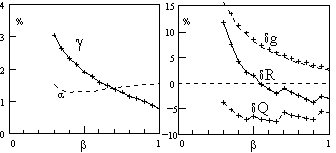
Figure 6 gives the characteristics of the coupling slots for different speed values. According to MAFIA results, varies approximately in 1/. The frequency detuning factor due to the slots volume (, defined as the relative difference between the 0-mode and a purely 2D cell) is almost constant ( 1.4%). In all cases, the slots actually improve the geometrical impedance (g>0), but this effect is more important for low speeds. On the other hand, the slots always reduce the quality factor. This effect does not seem to depend on : (Q-7%), but the result suffers from numerical noise probably due to the mesh approximation. The net result in shunt impedance is null for 0.6.

Influence of slots has been investigated on the first higher order modes. We computed the bandwidth of these modes in the "2-beans" and "4-petals" cases. As far as we investigated monopole and dipole modes under 1 GHz, we did not see any evidence of dangerous modes emerging. Table 1 gives the data of the TM110 mode (generally considered as the most dangerous one).

Table 1. TM110 mode coupling characteristics.

TM110	2 -beans 0 0				4-petals 0		single cell
g /m	245	245	238	238	228	241	238
f MHz	637	655	659	659	652	659	660
f	18		0.2		7

The 4-petals geometry has been computed with two other 3D electromagnetic codes: ANTIGONE [5] (which can use two solving methods: E or H), and SOPRANO [6] . The aim is not to compare absolute code performances, but rather to get more confidence in the results. As a matter of fact, the codes raw results are juxtaposed here without any consideration about meshing and solving methods, number of points, symmetry used, computation time, etc.

Single cell results. These may be compared with the ones of the well known 2D code SUPERFISH (Table 2). Numerical values are very close from each other, except for Q-value which seems underestimated by MAFIA.

Table. 2. Single-cell and 0-mode results with 3D codes (plus Superfish for single-cell)

single-cell	MHz	Q	g=R/Q	MHz	Q	g=R/Q
Superfish	361.37	40888	148.7	0-mode
Mafia	361.72	36271	146.8	356.72	40373	149.9
Anti- E gone H	360.17 361.69	40499 40609	150.7 145.8	355.05 356.33	44678 42517	152.8 147.5
Soprano	361.40	40058	147.2	356.35	44754	150.5

Table 3. -mode results with several 3D codes

-mode	MHz	Q	g=R/Q	%	Q %	g %
Mafia	351.81	34114	154.5	1.40	-5.95	+5.25
Anti- E gone H	350.43 351.22	37878 33753	156.2 151.3	1.31 1.45	-6.47 -16.9	+3.65 +3.77
Soprano	352.01	38755	155.0	1.23	-3.25	+5.26

Effects of coupling slots. According to results of table 3 (,Q,g), the slots effects are rather coherent. The only strong difference comes from the Q drop which is much more important according to ANTIGONE-H.

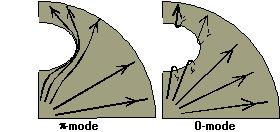
The quality factor drop may be interpreted as follows: the surface current lines, which are radial in the iris of a non coupled cell, have to deviate because of the coupling slot. This induces a current concentration on the slot edge in the -mode. In the 0-mode, the current lines do not deviate but cross through the slot to the next cell (See fig. 7) .

Until now, we have no explanation on geometrical impedance improvement due to slots. Actually, a small part of this effect (about one fifth of it) can be explained with transit time factor variation. As real cavity must be tuned anyway at the right frequency, this effect should be deduced by using the goal frequency (=2352 MHz) instead of the one of each mode in the impedance formula (eq. 3). This would lead to a conclusion a little less optimistic for g (about -1%), but as this correction should also be applied to the "2-beans" shape, the conclusion is unchanged.

A cold model experimentation is planned to settle the point of Q-factor drop, as code results do not totally agree.

The author thanks G. Le Meur from LAL (Orsay) who developed ANTIGONE and carried out the computations presented here. The author is debtful to C.Riley from Vector Fields Ltd (Oxford) for his processing with SOPRANO.

[1] M.Promé, "Conceptual studies for a high-power proton linac ", Lin. Acc. Conf. , Tsukuba, 1994, p.146.

[2] C.Bourat, "Structure CCL à 352 MHz et comparaison avec les structures à 704 MHz", Rapport Thomson DSM/DT/DIR CHB 003/95, 1995, p.2.

[3] P.Balleyguier et. al, "Study of a 433 MHz 3-cells cavity for FEL application", Europ. Part. Acc. Conf., Nice, 1990, p.910.

[4] I.Wilson and H.Henke, "The LEP main ring accelerating structure", CERN Report 89-09.

[5] G. Le Meur and F .Touze,"Priam/Antigone: a 2D/3D package for accelerator design", Eur. Part. Acc. Conf., London 1994, p.1321.

[6] D.Walsh, C.Emson and C.Riley, "Resonant cavity design using the Finite Element Method", Eur. Part. Acc. Conf., Sitges, 1996, (Proceedings to be published).