The TBNLC collider design uses Relativistic Klystron Two-Beam Accelerator (RK-TBA) units as the rf power source for a NLC-type linac at 11.4 GHz. In this paper we report on a simple analysis of using RK-TBA units as a rf power source for a CLIC-type linac at 30 GHz. The desired rf macropulse duration is less than 50 ns with a repetition rate of 600 Hz. We propose to use magnetic pulse-compression units driving ferrite-core induction cells for this system. Many elements of the TBNLC remain the same for a collider design at this higher frequency.

In this paper we described a short-pulse rf source that could be used to drive an electron-positron collider. We refer to this design as RK-CLIC. The high-gradient struc-tures being considered are about 1.5 times longer, with a longer fill time, than those that CLIC proposes for their 10-bunch collider design [1]. Each main linac accelerating structure requires 95 MW to produce an average loaded accelerating gradient of 80 MV/m. The structures are 42 cm long and 8 cm are allowed for pumping ports, flanges, etc., resulting in a 0.5 m spacing. Thus, the average grad-ient is 67 MV/m for a total main accelerator length of 15 km to produce a 1-TeV center-of-mass energy. The high-gradient linac beam profile is a 50 bunch train with 20 cm spacing. The linac will operate at 600 Hz to achieve a luminosity of 1034 cm-2 s-1. The rf pulse shape has a 17-ns linear ramp with a 33.7-ns flat top to produce a constant energy for all the bunches at the interaction region.

In analogy to the TBNLC [2], we propose that the high-gradient linac be powered by 50 RK-CLIC units. Each unit provides rf power for 300 meters of main linac. Similar to the TBNLC, each unit consists of the following major components: a 1.2-kA, 2.5-MeV induction injector, a beam modulation unit, an adiabatic capture section to accelerate and bunch the beam, the main rf power extraction unit, and an afterburner where power is extracted from the decelerating beam prior to the beam dump. At the entrance to the rf power extraction unit the beam has an average energy of 10 MeV and 1,120 A of rf current. 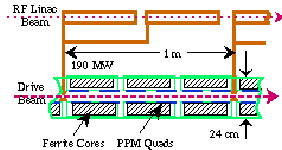A one meter section of the rf power extraction unit is shown in Fig. 1. Each rf power extraction unit is comprised of about 300 of these sections, and each section drives two high-gradient linac accelerating structures.

The drive beam dynamics issues of concern are beam transport, longitudinal bunch stability, and transverse beam instabilities.

Drive Beam Transport

We use permanent magnet quadrupoles in a FODO lattice for beam transport. The lattice period is 33.3 cm with a 60° phase advance per period to produce a 2-m betatron period. The ferrite magnets have a 800 G pole strength, 2.5 cm radius bore, and a 0.48 occupancy factor.

For a 500 '-mm-mr normalized edge emittance, the drive beam edge diameter should be about 3 mm. The aperture of the 30 GHz rf output structures is 6 mm. This places a high emphasis on the production and preservation of low emittance beams. The emittance requirement could be relaxed by increasing the drive beam energy.

Longitudinal Bunch Stability

We use a transverse chopper to initially modulate the drive beam as in the TBNLC design. However, other modulation schemes can be envisioned. The beam exits the chopper occupying a longitudinal phase of 240° and is compressed to 70° reaching an rf current of 1,120 A and an average current of 630 A.

In the rf power extraction unit, average beam energy is maintained at 10 MeV by 3 100-kV induction cells per 1-m section that restore the 190 MW of power extracted in the rf output structure. The synchrotron period (particle rotation in the rf bucket) in the extraction unit is approximately 30 m. The rf output structures are detuned to compensate for bunch lengthening effects. However, the shorter synchrotron wavelength and closer spacing of rf output structures should improve longitudinal stability relative to the TBNLC design.

Transverse Beam Instabilities

The beam dynamics for the low frequency, 2-4 GHz, transverse instability due to beam interaction with the induction acceleration gaps, should be the same as in the TBNLC. Landau damping from energy spread will suppress this instability. However, the lower emittance required for the RK-CLIC drive beam may require reducing the transverse impedance of the induction gap.

The high frequency, ~40 GHz, transverse instability due to higher order modes in the rf output structure, is a more difficult problem. There are twice the structures, and their transverse impedance is expected to be greater with respect to the TBNLC design. For the TBNLC, it was necessary to use the Betatron Node Scheme [3]. This scheme will remain valid for RK-CLIC where the structures are spaced at half Betatron wavelengths. The total effect should lead to an instability growth similar to that for the TBNLC, but perhaps requiring a higher tolerance on focusing field errors.

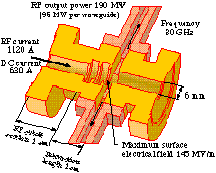
An illustration of the proposed RK-CLIC rf output structure is shown in Fig. 2. Direct scaling, i.e. geometrical dimensions are varied directly with wavelength, of the TBNLC three-cell traveling-wave output structure was used. The longitudinal impedance is invariant while the transverse impedance increases as w with this scaling [4].

The maximum surface field of the TBNLC rf output structure is predicted to be 75 MV/m for 360 MW output. At 190 MW, the surface field should reduce to 55 MV/m. Assuming the surface fields scale inversely with the aperture, we predict surface fields of 145 MV/m for the RK-CLIC structure generating 190 MW. Experiments on relativistic klystrons, with similar pulse lengths to the RK-CLIC, indicate that the rf output structures can be safely operated with 100 MV/m surface fields at 11.4 Ghz [5]. Assuming the breakdown limit for a copper structure scales as the square root of the frequency, we can expect to safely operate up to 160 MV/m fields at 30 GHz.

The induction cell voltage is 100 kV/cell as in the TBNLC. The pulse length at the FWHM of the voltage waveform is taken as 50 ns. The Ceramic Magnetics CMD-5005 ferrite is used for the accelerator cores. The core consists of a 25 cm long tube of ferrite with a 8 cm inner diameter. Assuming a DB of 0.65 T, the outer diameter of the ferrite is about 14.2 cm.

The energy loss per volume at our parameters for the ferrite is estimated to be 600 J/m3. Thus, ~ 1.6 J is lost in the ferrite per pulse. The energy required for the beam is 1/3 (3 induction cells per rf output) of 190 MW · 50 ns or 3.17 J. The losses associated with capacitance and stray induction for these short pulses can limit efficiency. If we assume a capacitance, C, of 20 pf, then the energy loss is C · V2/2 = 0.1 J. Thus, the efficiency for the cell is:

hc = 3.17/(3.17 + 1.6 + 0.1) = 65%. (1)

A smaller inner radius would reduce core losses, but increase the transverse impedance of the induction cell gaps. New core materials could lead to better efficiency and lower costs. Within the limitations of materials that we have tested, the easiest way to improve efficiency is to increase the pulse length. In Fig. 3 the efficiency of the induction cell for three different core materials are plotted as functions of pulse length. The voltage, inner radius, and length of the core were fixed at the RK-CLIC design values given above. For pulses shorter than 50 ns, the CMD-5005 ferrite is the preferred material of those examined. Over 50 ns, the Allied-Signal METGLAS® alloy 2714AS shows improved efficiency. Doubling the pulse length increases the core efficiency by about 8%.

We cannot reduce the rise time of thyratron switching, used in the TBNLC design, sufficiently to obtain a 17-ns rise time. Also, the pulsed power system proposed in the TBNLC design is not suitable for a 600 Hz repetition rate.

We are proposing magnetic pulse compression and switching [6]. This technique has been demonstrated at high repetition rates and with fast rise times in other applications [7]. Ability to cool the ferrite cores in the switches/compressors and the pulse power units will need design effort, but multiple kHz operation is possible.

A preliminary design for a three stage magnetic pulse compressor was performed to assist in estimating cost and efficiency. The magnetic compressor/switch parameters used in this design are listed in Table 1. Energy storage for the third stage consists of a 0.84-m long, water-filled Blumlein line. The first two stages use Strontium-Titanate capacitors. The long charge time of the first stage allows the use of a solid state system for the initial triggering.

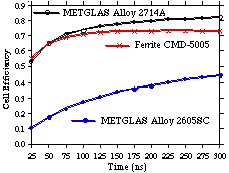
Table 1. Magnetic Compressor Parameters.

Stage	Charge Discharge	Gain	Switching Core / Turns	Core Efficiency
1st	7.5 µs 1.25 µs	6	5.8 kG - 2605SC / 20	0.983
2nd	1.25 µs 250 ns	5	20.8 kG - 2714AS / 6	0.984
3rd	250 ns 50 ns	5	26.8 kG - 2714AS / 1	0.980

The advantage of this magnetic compressor system is that it is totally solid state. It should have high-reliability, long lifetime, good efficiency, and be capable of kHz operation. A drawback of the system is that it is difficult to adjust the voltage wave shapes to obtain different accelerating gradients. Fast correction circuits interspersed in the system could be used to correct for errors.

Where possible, comparable efficiencies for similar components with conventional klystrons or the TBNLC are used. We have based estimates on current technology.

(1) DC Power Supplies - Conventional 60 Hz 3 phase full wave rectifier with filter supplies will be used. Estimated efficiency is 93%.

(2) Command Resonant Charging (CRC) System - A solid state CRC system with estimated efficiency of 96%.

(3) Pulsed Power Modulator - Magnetic compression power losses are due primarily to three components, core losses, ohmic losses in the Blumlein water, and capacitors. Losses due to the cooling system are included under auxiliary power. Table 1 lists core efficiencies. Assuming the same ratio between the outer and middle conductors radii as between the middle and inner, the energy loss in the water can be expressed as:

, where (2)

L is the length (cm) of the Blumlein, Vo/Io is the applied voltage (V)/current (A) to the load, r is water resistivity (_-cm), er is relative permittivity, and Dt is charging time. In our design, L = 84 cm, Vo = 25 kV, Io = 17 kA, er is 80, r = 8 M_-cm and Dt is 250 ns for an energy loss of 0.094 J. The efficiency of the capacitors is estimated at 98%. Total estimated efficiency is 92%.

(4) Induction Cells - As described above, the cell efficiency should be about 65% for 50 ns pulses.

(5) Drive beam (pulse fall time) - As in the TBNLC, we plan to utilize the rise time of the current pulse. As an estimate of the energy to drive the core during the fall time, we allowed 300 A core current (average core current used for induction cell losses) times 20 ns fall time times one half of 100 kV or 0.3 J. This amount also includes the 0.1 J stored in the gap capacitance. Thus, actual losses during the fall time not previously accounted for are only 0.2 J giving an efficiency of 94%.

(6) Drive beam to rf - The conversion losses of drive beam to rf power are due to losses at the front of the relativistic klystron, primarily in the chopper, and residual beam power lost in the dump. This will be the same as for the TBNLC design, about 90%.

(7) Auxiliary power - This miscellaneous category accounts for losses in systems such as cooling fluids, vacuum, etc. These losses are estimated to be 80 kW. At 600 Hz this represents an efficiency of 0.96.

To summarize, the estimated efficiencies are:

Component efficiency

Power supplies 0.93

CRC 0.96

Modulator 0.92

Induction cells 0.65

Drive beam (fall time) 0.94

Drive beam to rf 0.90

Auxiliary power 0.96

Total wall plug to rf efficiency 0.43

A preliminary study for a 30 GHz linear collider using the CLIC high-gradient linac and scaling of the relativistic klystron (RK) used in the TBNLC design was performed. The result was positive with an estimated wall plug to rf power efficiency of 43%. The rf to beam efficiency for the CLIC parameters used is 67% for a total efficiency of 29%. No attempt was made to optimize parameters for the combined rf power source/CLIC, e.g. gradient, and pulse length. However, increasing the pulse length could substantially improve the efficiency of the (RK) while also improving the efficiency of rf to beam conversion.

A very approximate costing study was performed. The cost of the 30 GHz RK-CLIC is practically the same as for the 11.4 GHz TBNLC. Savings due to the shorter pulse length and reduced energy per pulse are balanced by the additional cost of doubling the number of output structures.

We thank S. Chattopadhyay and A. Sessler for their support and guidance. We thank J-P Delahaye, C. Johnson, L. Thorndahl, and I. Wilson for their assistance in determining the performance and rf requirements for the CLIC architecture.

[1] CLIC Note 295 22.01.1996, "CLIC/RK-TBA Collaboration Meeting," Novotel-Geneva Airport, 15-16 Jan. 1996.

[2] "An RF Power Source Upgrade to the NLC Based on the Relativistic-Klystron Two-Beam-Accelerator Concept," Appendix A of the Zeroth-Order Design Report for the Next Linear Collider, SLAC Report 474, Stanford University, Stanford, CA, May 1996.

[3] G. Giordano, et al., "Beam Dynamics Issues in an Extended Relativistic Klystron," Proc. 1995 IEEE Part. Acc. Conf., pp.740

[4] A. Chao, "Physics of Collective Beam Instabilities in High Energy Accelerators," NY: John Wiley & Sons, 1993, pp. 87-89.

[5] G.A. Westenskow and T.L. Houck, "Relativistic Klystron Two-Beam Accelerator," IEEE Trans. on Plasma Sci., 22, 750 (1994).

[6] D.L. Birx, et al., Basic Principles Governing the Design of Magnetic Switches, UCID-18831, Lawrence Livermore National Laboratory, Livermore, CA, November, 1980.

[7] E.G. Cook, et al., "High Average Power Magnetic Modular for Copper Lasers," UCRL-JC-105816, Lawrence Livermore National Laboratory, Livermore, CA, June 1991

*The work was performed under the auspices of the U.S. Department of Energy by LLNL under contract W-7405-ENG-48 and by LBNL under contract AC03-76SF00098.