Apart from very computer time consuming PPI routines (Particle to Particle Interaction, e.g. [1] ), all previous space charge routines require some kind of symmetry. A new routine, not requiring symmetry, is being developed. It offers fast computation and is little sensitive to statistical noise. It could become a good tool for studying halo formation phenomena.

Almost all presently available space charge routines require some form of symmetry. The common SCHEFF routine [1][2], transforms the density distribution into a rotationally symmetrical one, where the field is computed and linearly corrected inside an elliptical cylinder. The outside density distribution is obtained using a different method, and discontinuities appear. Moreover it is very sensitive to statistical noise. In the SC3DELP [3] and MAPRO [4] routines, the bunched beam is assumed to have an ellipsoidal symmetry. The former SCHERM routine [2], represents the non-symmetrical longitudinal shape of the bunch with two or three ellipsoids. However it keeps in the transverse direction an elliptical profile. The MOTION routine [5] treats the two transverse directions x and y independently.

The present work suggests a new type of approach, offering fast computation without the need of strict symmetry.

Three dimensional representation of the bunch

The three dimensional representation of the charge distribution of the bunch is made with Hermite expansions. As shown in [2], one can obtain the integrated charge density along one axis in the form of a Hermite series expansion :

(1)

a is the r.m.s. dimension of the bunch along the x axis and A_i is defined as :

(2)

where q is the charge of the macroparticle. Analogous relations are valid in the y and z directions, with b and c as respective r.m.s. dimensions. In these expressions the coordinates are taken with respect to the centre of gravity of the bunch; N is the number of particles in the bunch. As and it turns out that .

Most functions of a coordinate can be represented with a Hermite series expansion. For instance, one may be interested in the variation a(z) of the transverse r.m.s. dimension in x of the bunch along the z axis. To do so one can compute the following function of z :

(3)

where

(4)

One obtains :

(5)

A_k is given by :

(6)

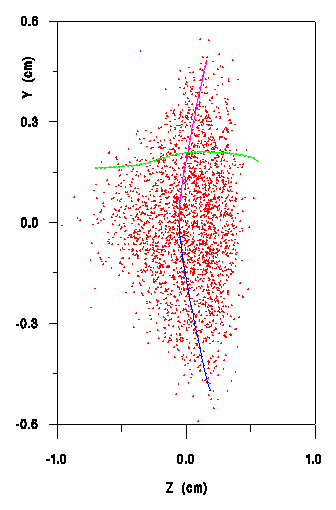
Similarly, one could compute the variation of the centre of gravity in z along the x axis (ditto for the y axis). One gets :

(7)

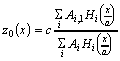
with

(8)

and analogous relations for z(y). An example is given in Fig.1.

In the above derivation the terms A_2,k and A_i,1 of a two dimensional Hermite series expansion have been introduced. Such an expansion can be extended to three dimensions, giving the local density distribution (x,y,z) :

(9)

with

(10)

As above one has A₁₀₀=A₀₁₀=A₀₀₁=A₂₀₀=A₀₂₀=A₀₀₂=0. If the three axes are chosen such that , the corresponding terms A₁₁₀, A₀₁₁ and A₁₀₁ are also zero. This last condition is not necessary; would it be needed one can straighten up the axes by rotation. The main term A₀₀₀ is such that :

(11)

The charge density distribution in a bunch can be considered to be a Gaussian :

(12)

corrected by various terms (coefficients A_ijk in eq.9), each of them of total charge zero. In practice most of these terms are in the range of a few per cent or less of the fundamental term A₀₀₀, only a few ones are slightly above 10 %.

The field due to the Gaussian term (eq.12) is computed by numerical integration as explained in [2], but the macroparticle charge density contains a single term only and therefore computer time remains small. For the other terms the method introduces approximate expressions of the field, good in the part of the bunch where most of the particles lie, but less correct at large distances where the field is anyway very weak. According to the Laplace-Poisson relation :

(13)

and the following property :

(14)

one can take for the charge term , with :

yielding to the following field components :

(15)

(16)

(17)

a, b, c define the r. m. s. size of the bunch, and . These , and , which depend on a, b and c but also on i, j and k, have to be optimized for each term. At large distance the real field vanishes as r^-n ( with n>2 ) instead of exponentially. However, the error made is not significant.

A difficulty appears in the eq.(15), (16) and (17) for i, j or k = 0 : the integral of , which corresponds to the error function, does not go down to zero at infinity. It is therefore replaced by a polynomial equivalent to the above integral over most of the interval, but going to zero at infinity.

Since the major interest of this new method is to compute space charge fields in the absence of any symmetry, comparisons have been made with a PPI routine in order to check its validity.

In order to explain the differences which could arise in these comparisons, it is essential to examine the limits of the PPI routine such as its sensitivity to statistical noise and to the so-called "stopping distance", which avoids that the field becomes infinite when the macroparticles are too close to each other.

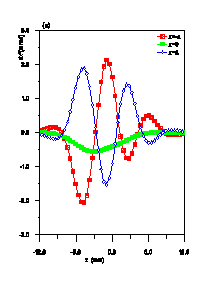
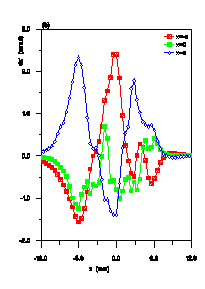
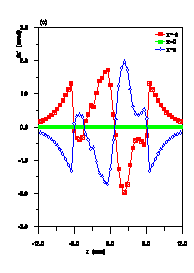
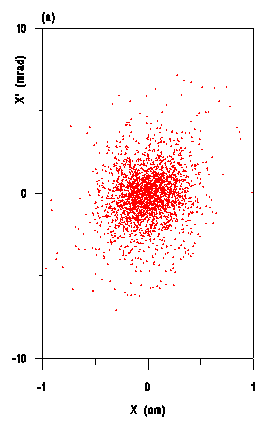
In Figures 2, 3 and 4 comparisons between the new space charge routine and previous ones for the CERN proton linac at 200 mA are shown for different positions along the machine for 5000 particles. In Fig.4 one clearly observe the differences in particle distributions between the results obtained with the new space charge routine and SCHEFF at the output of the CERN proton linac. The emittances and transmissions , however , yield to very similar values.

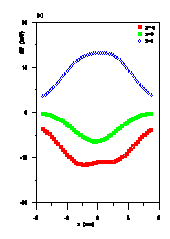
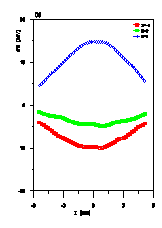
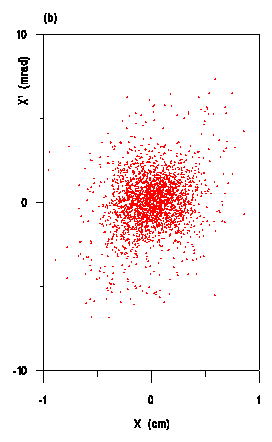
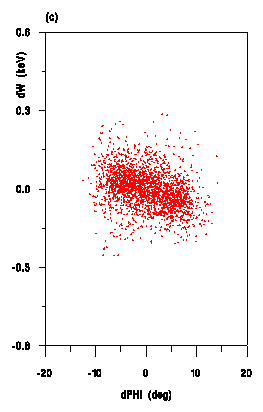
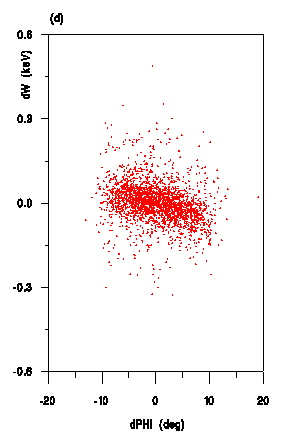
This new space charge method is very promising the design and operation of high intensity linacs. The computing time needed with the new method is significantly shorter than any other presently available routine. Some possible refinements of the present method are still being studied. This routine might also be used for cyclotrons.

We thank H. Haseroth and W. Pirkl from CERN for their interest and support.

[1] F. Guy, "3-D Space Charge Subroutines for PARMILA", Los Alamos Group AT-1 Memorandum AT-1:85:90,March 6, (1985)
[2] P.Lapostolle, A.M.Lombardi, E.Tanke, S.Valero, R.W.Garnett, T.P.Wangler, "A Modified Space Charge Routine for High Intensity Bunched Beams", NIM A, Vol. 379, pp. 21-40, September 1996

[3] R.W. Garnett and T.P. Wangler, "Space-Charge Calculation for Bunched Beams", IEEE PAC Conf., San Francisco (1991),p.330

[4] M. Martini, M Promé, "Computer Studies of Beam Dynamics in a Proton Linear Accelerator with Space Charge", Part. Acc. 1971, Vol.2, pp. 289-299

[5] K. Mittag, D. Sanitz, "MOTION, a Versatile Multiparticle Simulation Code", Linac Conf. Proc., Santa Fe, LA-9234-C, p.156 (1981)