High-power proton linacs for nuclear materials transmutation and production, and new accelerator-driven neutron spallation sources must be designed to control beam-halo formation, which leads to beam loss. The study of particle-core models is leading to a better understanding of the causes and characteristics of beam halo produced by space-charge forces in rms mismatched beams. Detailed studies of the models have resulted in predictions of the dependence of the maximum amplitude of halo particles on a mismatch parameter and on the space-charge tune-depression ratio. Scaling formulas have been derived which will provide guidance for choosing the aperture radius to contain the halo without loss.

High-intensity proton linacs are being proposed for new projects around the world, especially for tritium production, and for pulsed spallation neutron sources. Typical requirements for these linacs include high peak beam currents of about 100 mA, and final energies of about 1 GeV. For these applications high availability is demanded. High availability requires very low beam-loss to avoid radioactivation of the accelerator and to allow hands-on maintenance that will keep the mean repair and maintenance times short. This challenge will require a greater understanding of the evolution of the beam distribution, including the low-density beam halo.

Numerical studies have established rms mismatch as a major cause of emittance and halo growth.1,2,3 The particle-core model4,5,6 for a continuous beam has contributed to an understanding of the underlying causes of halo formation from mismatched beams. We have recently developed a particle-core model for the case of a spherical bunch. In these models the space-charge field from a mismatched beam core, propagating in a uniform linear focusing channel, is represented by a hard-edged, spatially-uniform density distribution that oscillates radially in the symmetric breathing mode. The amplitude of the breathing mode is directly related to the initial rms mismatch of the beam. The dynamics of the outer halo particles are determined by the external focusing force and the repulsive space-charge force from the oscillating core. The behavior of these particles is studied in the model by representing the outer halo particles with single particles that oscillate through the core, and interact with it. We will restrict our treatment to particles with zero angular momentum. The equations for the models can be expressed in a dimensionless form. The equation of motion of the core radius is the envelope equation

. (1)

The matched beam size is the solution of Eq.1 when d2r/dt2 = 0. The equation of motion of a particle inside the core radius is

, (2a)

and outside the core is

. (2b)

The upper expression in the bracket for each of the above equations is the space-charge term for the continuous beam and the bottom expression is for the spherical bunch. The quantities r and x are dimensionless displacements taken relative to the radius R0 of the matched core, the independent variable is t = k0z, where z is the axial distance and k0 is the zero-current phase advance per unit length without space charge, and h = k/k0 is the space-charge tune depression. It can be shown that , where e is the unnormalized rms emittance. For the cylindrical beam, , where the quantity K is the generalized perveance, related to the particle charge q, mass m, velocity b, relativistic mass factor g, and beam current I, by , and for the spherical bunch with number of particles N per bunch, , where . The degree of mismatch is measured by the mismatch parameter m, defined as the ratio of the initial beam radius to the radius of the matched beam; an rms matched beam has m = 1.

The particle phase-space motion is complicated, because of the time-dependent space-charge force, which is nonlinear when the particles are outside the core. The particles can either gain or lose energy, depending on the phase of the particle motion relative to the phase of the core oscillation. The particles slowly gain or lose energy as a result of a series of kicks. It has been found that a parametric resonance exists6 such that the largest energy transfer occurs when the particle frequency is about one half the core frequency. The particle frequencies depend on the amplitude, because of the nonlinear space-charge force, and not all particles can be locked into resonance. The motion is most conveniently described by showing a stroboscopic or Poincare map, shown in Fig.1, in which phase space for the continuous beam with m = 1.5, and h = 0.5, and is plotted for an initial array of test particles, once per core oscillation cycle. An initial distribution of halo particles is distributed regularly along the x and axes, and the strobe time is taken when the core radius is minimum. In Fig.2 we show the corresponding stroboscopic plot for the mismatched spherical bunch.

Three distinct regions are observed in Figs.1 and 2, defined by a separatrix. First, there is the inner region, which may be called a core-dominated region. Particles with trajectories in this region spend most of their time inside the core, where the frequencies of motion are too small for a strong resonant energy transfer with the core. There is an outer region, which may be called the focusing-dominated region, in which the particles spend most of their time outside the core. The motion of these particles is mostly determined by the external focusing force, and these particles have an oscillation frequency too high to have resonant energy transfer with the core. Finally, there are the regions surrounding two fixed points on the x axis, one on each side of the origin. In these regions the particle oscillation frequencies are close to one half the core frequency, and the parametric resonance produces large energy transfers. The amplitude growth for the resonant particles is self limiting, because of the nonlinearity. A maximum resonant-particle amplitude exists, which depends on the amplitude of the core breathing mode, which is related to the initial rms mismatch of the beam. The general features of the particle dynamics appear to be insensitive to the details of the assumed core distribution. For example, a similar stroboscopic plot is obtained, if the distribution of the core is changed from uniform to Gaussian.7 The appearance of the stroboscopic plots is found to be very insensitive to the tune depression h. Chaos, observed as a breakup of the separatrix, can be seen for values of the space-charge tune depression ratio, below about 0.4.

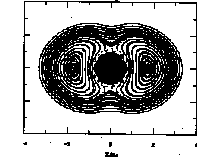
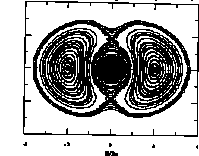
Our hypothesis is that if we inject a realistic beam with a tail that is rms mismatched to the focusing lattice, the particles in the tail that fall under the influence of the parametric resonance with the breathing mode will be driven to large amplitudes, and produce the halo. We cannot rule out the possibility that beam instabilities might also cause additional particles from the core region to move across the separatrix into the resonance dominated region and add to the halo. That only a small percentage of the particles comprises the halo in a real beam, can be explained because the percentage of the particles in the tail of the injected beam that fall within the resonance region is small. Low tune depressions and accompanying chaos can be expected to increase the population of the halo, because then, more particles in the injected beam can be influenced by the resonance.

A significant prediction of the particle-core model is that for given values of m and h, there is a maximum amplitude for the resonantly-driven particles that form the halo, given by the location of the outermost point of the separatrix. The maximum amplitudes have been calculated as a function of m and for h = 0.5 and 0.9 from the numerical solution of Eqs.1 and 2, and are shown in Fig. 3. Figure 3 shows that the spherical bunch case leads to larger maximum amplitudes than for the continuous beam. We interpret the results of the two models as upper and lower limits in a smooth approximation for the average values of the maximum amplitudes of ellipsoidal bunches, because in proton linacs, the longitudinal semiaxis of the bunches is usually larger than the radius. From Fig.3, it can be seen that the maximum amplitude, as described in the normalized or dimensionless form, is very insensitive to h. The normalized maximum amplitude is well described by an approximate empirical formula

, (3)

where xmax is the maximum resonant particle amplitude, a is the matched rms beam size, which is identified in the model with the rms size of the core, and A and B are weak functions of the tune depression h. In the range , and , we obtain least-square-fitted values of A and B. These are given in Table 1.

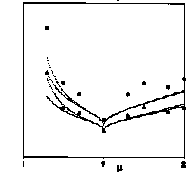
Table 1

Core	h	A	B
Cylindrical	0.5	3.97	3.83
Cylindrical	0.9	3.91	4.25
Sphere	0.5	4.87	5.30
Sphere	0.9	4.81	5.56

Equation 3 is not a good approximation for mismatches very close to m = 1, where, as m approaches 1, xmax/a rapidly approaches 2 for the continuous beam, and for the spherical bunch.

We have determined a characteristic time scale from the particle-core model for particle motion in the resonance region. Unambiguous results are obtained by calculating the period for small-amplitude oscillations about a stable fixed point on the x axis of the stroboscopic plots. Particle periods for the continuous beam, obtained for m = 1.5, are about 10 breathing-mode periods for h < 0.4, and for h > 0.6, the particle period increases rapidly with h. If we interpret the particle periods from the particle-core model as the characteristic growth time for the halo, we observe that the growth time for the halo is reduced significantly as h decreases from 0.9 to 0.6. The wave-number kb for the breathing mode can be obtained from the expressions for the phase advance per unit length, for the continuous beam, and for the spherical bunch.

In a real linac, additional effects that are not included in the particle-core model, must be accounted for, such as beam-envelope flutter associated with a quadrupole focusing system, acceleration, and the influence of other modes of the mismatched beam. We have conducted a test of the predictions of the particle-core model, by carrying out PARMILA simulations, using an r-z space-charge mesh with individual runs at 105 particles per run. The linac used for the test was a 217- to 1700-MeV section of a superconducting proton linac with variable tune depressions and with transverse focusing from a singlet quadrupole FODO lattice. An initial 6-D waterbag distribution (uniformly-filled 6-D ellipsoid) was used, and the beam was given the same initial mismatch parameter m in all three planes, which was varied from run to run. Simulation studies of beam mismatch have shown that this type of mismatch appears to produce the most extended halo. The maximum particle displacement was determined at the center of every quadrupole, and the largest of these maxima for each m was plotted in Fig.3. Because of the flutter associated with the periodic quadrupole lattice, the models should be compared with the maximum displacement smoothed or averaged over the lattice period, which we have also presented in the Figure. The smoothed PARMILA points in Fig. 3 are observed to lie between the sphere and cylinder models, as would be expected for beam bunchs that are approximate prolate ellipsoids. Considering the simplicity of the models, we believe that the agreement of the maximum amplitudes from the models and the simulations is remarkably good, and it supports the hypothesis that the breathing mode is a main driver of the beam halo in a linac. As a further test of the importance of the breathing mode, we have plotted the rms transverse cross-sectional area of the beam as a function of energy along the linac, to search for the area oscillations that would be expected if the breathing mode was excited. Indeed, area oscillations are observed with a period that is consistent with the theoretically expected breathing-mode values. We note that these simulations should be repeated using a 3-D mesh to ensure that we have not excluded any modes in the r-z simulations that may be important.

Work during the past several years has led to the hypothesis that beam mismatch will be the main cause of beam halo in the new linacs. If we assume that the breathing mode, is mainly responsible for the halo, we can use the particle-core models to make quantitative predictions about the halo that is formed. The particle-core models, one for a continuous beam and one for a spherical bunch, predict that the halo will be limited to a maximum amplitude, which depends mostly on the strength of the initial mismatch. We interpret the predictions of the two models as establishing lower and upper bounds of the halo amplitude for a prolate ellipsoidal bunch in a linac. Simulation results for a realistic linac are found to produce smoothed maximum amplitude values that are consistent with the models, and provide additional evidence that the breathing mode is the most important mode producing the halo. To keep the halo small, one needs to match the beam as well as possible, and keep the rms beam size small by keeping e small and k0 large. We note that additional effects can contribute to beam halo, such as intrabeam scattering, beam-residual gas scattering, and image-charge effects. However, these effects are expected to be usually less serious than beam mismatch.

The authors acknowledge helpful discussions with R. Gluckstern and I. Hofmann.

* Work supported by the US Dept. of Energy.

1. A. Cucchetti, M. Reiser, and T. P. Wangler, Proc. 1991 Part. Accel. Conf., IEEE Cat. No. 91CH3038-7 (1991) 251.

2. M. Reiser, Proc. 1991 Part. Accel. Conf., IEEE Cat. No. 91CH3038-7 (1991) 2497.

3. R. D. Ryne and T. P. Wangler, Int. Conf. on Accelerator-Driven Transmutation Technology, Las Vegas, NV, AIP Conf. Proc. 346, 383.

4. J. S. O'Connell, T. P. Wangler, R. S. Mills, and K. R. Crandall, Proc. 1993 Part. Accel. Conf.,Washington, DC(1993) 3657.

5. J. M. Lagniel, Nucl. Inst. Meth. A345(1994) 46; A345(1994) 405.

6. R. L. Gluckstern, Phys. Rev. Lett. 73(1994) 1247.

7. Thomas P. Wangler, "Dynamics of Beam Halo in Mismatched High-Current Charged-Particle Beams," Los Alamos Report LA-UR-94-1135, March 29, 1994.