Beam halo is a critical issue in the design of high-intensity ion accelerators for neutron spallation, materials studies and transmutation technologies. A new particle-core model, which treats accelerating bunched beams, is described. The core is a uniformly-filled 3-D ellipsoid in an azimuthally-symmetric linac with linear, continuous transverse focusing. The envelope equations are solved for the length L and radius R of the core, by treating the average longitudinal focusing forces as linear and continuous also. Core mismatch yields coupled oscillations of L and R with two distinct frequencies. The Hamiltonian for test-particles near the core is derived, including the oscillating space charge forces and a realistic Fourier expansion of the accelerating fields. Changes in linac parameters and beam energy are assumed adiabatic.

Beam losses of as little as 1 part in 108 per meter can lead to unacceptable activation levels in beamline components for proposed high-current, high-intensity ion linacs. Because of the finite number of macroparticles that can be used in a realistic beam dynamics simulation, it is only possible to set an upper bound on the levels of particle loss, and it is unlikely that such numerical simulations can resolve beam losses at this very low level.

Given this fundamental limitation, simple models are very important for developing physical insight into the causes of beam halo and particle loss. The well-known particle-core model [1], for example, has been used to illustrate how beam mismatch can lead to halo development. However, the particle-core model is limited to coasting unbunched beams, which is a significant departure from the actual problem of bunched beams in the accelerating fields of a linac.

We propose a longitudinal analog to the particle-core model for the purpose of studying the halo dynamics of test-particles interacting with a bunched beam in an RF linac. This model will be useful primarily for exploring regions of phase space outside of the core that are sparsely populated. Such regions can become populated at the low-energy end of a linac: for example, ~10% of the beam from a typical ion source exhibits strong transverse aberrations, and bunching of the beam in an RFQ can lead to a tenuous longitudinal halo.

The core is assumed to be an azimuthally symmetric 3-D ellipsoid with a uniform distribution of particles, which leads to linear space charge fields inside the core. The transverse and longitudinal focusing forces are assumed to be linear and continuous. To further simplify the form of the space charge fields, free space boundary conditions are assumed and the condition 0.8 < g L / R < 4 is imposed, which is consistent with moderately relativistic ions with typical bunch shapes in large-bore cavities (see Ref. [2] for further discussion).

The core is treated as though it were moving with constant velocity; energy and velocity increases are treated as adiabatic changes. Space charge fields inside the core are linear and have the form (see e.g. Ref. [2]):

;

. Eq. (1)

where I0 is the characteristic current. Space charge fields outside the core fall off nonlinearly.

In treating the RF fields, the geometry of a DTL is used, and the Fourier expansion of the RF fields is assumed to be symmetric between the drift tubes. The accelerating component of the RF fields is assumed to be small so the beam energy increases adiabatically. The longitudinal field has the form:

Eq. (2)

where , I0 is the zeroth order modi-fied Bessel function, and we are assuming a DTL geometry as shown below in Fig. 1. The radial electric field and azimuthal magnetic field have similar forms.

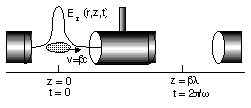
Given the assumed uniform transverse focusing fields, the space charge defocusing, the average longitudinal focusing calculated from Eq. (2), and the beam emittances, the dynamical equations for the core length L and radius R are readily obtained, as is shown on p. 449 of Ref. [2]. The transverse and longitudinal equations are coupled by space charge, and the equilibrium values, L0 and R0, must be obtained numerically.

We integrated the resulting test-particle equations of motion for a few trajectories through 500 DTL gaps, assuming physical parameters appropriate for a high-current D+ DTL, as shown in Table 1. The trajectories are plotted as Poincaré surfaces of section, with the phase space locations shown each time the trajectory reaches the center of a gap.

Table 1: Parameters used in Simulations

Current	100 mA
Frequency	175 MHz
Kinetic Energy	10 MeV
Relativistic factors: b; g	0.1; 1
Cell length: bl	18 cm
Phase advances: sx0; sx	60 deg ; 48 deg
sz0; sz	15 deg ; 11 deg
Bunch size: L0 ; R0	1 cm ; 0.2 cm
RMS emittance: ex	3 mm-mR (unnormalized)
ez	6 mm-mR = 0.24 deg-MeV
ETL; T; fs	0.23 MV; 0.8; -p/2

Figure 2 shows a surface of section for four trajectories. The innermost trajectory is well inside the core; the second one has an amplitude just less than L0; the third oscillates well outside of the core; and the outermost trajectory is near the boundary of stable motion. Each trajectory is moving along the accelerator axis, with no transverse motion. In this and following figures, the spatial variables X and dZ have been normalized to bl, Vx has been normalized to bc, and dVz is the relative momentum spread dp/p.

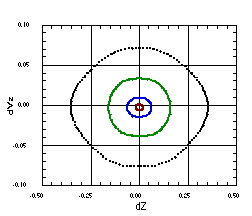
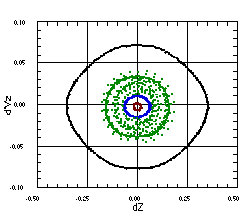
Figure 3 shows surfaces of section for four trajectories with the same longitudinal initial conditions, but each with an initial value of X=0.6R0. The two trajectories inside the core and the outermost trajectory remain stable, but nonlinear coupling between the transverse and longitudinal motion of the remaining trajectory have resulted in chaotic motion. As it spirals in longitudinally (upper plot) it spirals out transversely (lower plot) to large amplitudes.

Assuming small beam mismatch, the actual values of R and L differ from the equilibrium values as follows:

; ; Eq. (3)

where . Linearizing and solving the coupled differential equations leads to coupled mismatch oscillations of the form:

;

; Eq. (4)

where C+ and C- are complicated functions of the physical parameters, while A+ and A- are determined by the initial values of r and l.

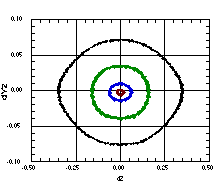
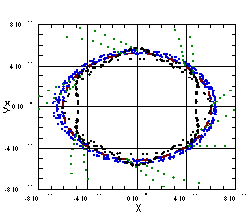
Figure 4 shows the result of mismatching the beam, when there is no transverse motion. The initial values of r and l were 0.1 and -0.1, respectively. For this case, the space charge coupling is relatively weak, and l oscillates approximately once every 3 RF periods, while R oscillates approximately once every 25 RF periods. Figure 4 shows that these oscillations have broken the third ring into a chain of 26 islands.

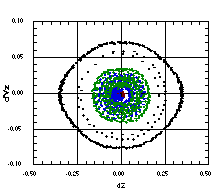
Figure 5 shows surfaces of section for four trajectories with the same longitudinal initial conditions, but each with an initial value of X=0.6R0. Only the innermost trajectory remains stable under the combined effects of beam mismatch and transverse/longitudinal coupling. The other three trajectories spiral inward longitudinally as they are driven outward transversely to maximum radii of 20 times the beam radius.

At present, the test-particle equations of motion for our proposed longitudinal particle-core model have only been studied numerically, but a limited analytical treatment should be possible. The transverse motion is predominantly linear, at least initially. Also, the transverse motion is much faster than the longitudinal motion, and this separation of time scales can be used to develop a perturbative treatment of the coupling between transverse and longitudinal motion. A third time scale exists, because change in the physical parameters is slow compared to the longitudinal motion. The two primary difficulties are the treatment of 1) space charge nonlinearities outside of the core, and 2) the rapidly oscillating (i.e. nonresonant) components of the RF fields.

The model studied here requires further testing and refinement. For simplicity, acceleration was ignored, but slow acceleration might play a stabilizing role by making resonances between the transverse and longitudinal motion temporary. The trajectories we studied had no motion in the y-plane, which implies zero angular momentum; finite angular momentum might also play a stabilizing role. Finally, the dynamics may be sensitive to the detailed treatment of the RF fields. We considered only 4 Fourier modes.

The author thanks Michael F. Reusch and John R. Cary for useful discussions. This work is supported by Northrop Grumman Corporation.

[1] J. S. O'Connell, T. P. Wangler, R. S. Mills and K. R. Crandall, Proc. 1993 Part. Accel. Conf. (Washington DC, 1993), p. 3657.

[2] M. Reiser, Theory and Design of Charged Particle Beams (John Wiley and Sons, New York, 1994).