In recent years, there has been increasing interest
in short electron bunches for different applications such as short
wavelength FELs, linear colliders, and advanced accelerators such
as laser or plasma wakefield accelerators. One would like to meet
various requirements such as high peak current, low momentum spread,
high luminosity, small ratio of bunch length to plasma wavelength,
and accurate timing. Meanwhile, recent development and advances
in RF photoinjectors and various bunching schemes make it possible
to generate very short electron bunches. Measuring the longitudinal
profile and monitoring bunch length are critical to understand
the bunching process and longitudinal beam dynamics, and to commission
and operate such short bunch machines. In this paper, several
commonly used measurement techniques for subpicosecond bunches
and their relative advantages and disadvantages are discussed.
As examples, bunch length related measurements at Jefferson Lab
are presented. At Jefferson Lab, bunch lengths as short as 84
fs have been systematically measured using a zero-phasing technique.
A highly sensitive Coherent Synchrotron Radiation (CSR) detector
has been developed to noninvasively monitor bunch length for low
charge bunches. Phase transfer function measurements provide a
means of correcting RF phase drifts and reproducing RF phases
to within a couple of tenths of a degree. The measurement results
are in excellent agreement with simulations. A comprehensive bunch
length control scheme is presented.
Interest in short bunches are driven by many applications such as short wavelength FELs, linear colliders, advanced high frequency accelerator development such as laser or plasma wakefield accelerators, and Compton backscattering X-ray sources [1-3]. Much progress has been made on photoinjectors and different magnetic and RF bunching schemes, and with simulation tools to produce very short bunches [4-7]. Electron linacs have the advantage of producing shorter bunches compared to circular machines. Bunch lengths less than 100 fs have been reported for low charge bunches [7-8]. Subpicosecond bunches with high charge per bunch have also been achieved [6, 9]. Recently a 1 ps bunch was reported for the circular machine at ESRF [10]. Bunch length measurement becomes essential to characterize, tune, commission, and operate such short bunch accelerators.
In this paper, several commonly used techniques for
measuring short bunches are briefly described. Then three bunch
length related measurements at Jefferson Lab: phase transfer function
measurement, zero phasing measurement, and monitoring CSR, are
presented in detail, followed by a summary. The bunch length is
defined by the rms size of the longitudinal distribution and subpicosecond
bunches are referred to as "short".
One conventional technique uses transverse deflecting RF cavities or a streak camera to measure short bunches in the time domain [11]. This method provides bunch length and longitudinal profile information. Using dual sweeping options, bunch-to-bunch resolution can be achieved at the expense of single bunch resolution. Using a L-band RF deflecting cavity, a few tenths of a picosecond resolution has been reported by the LANL group [6]. High resolution is reported for commercially available streak cameras by the vendor specifications [11]. Though the resolution of streak cameras is continuously improving, their high cost is still a primary concern. Also, due to their operational complexity these devices require significant amount of experience and special equipment for calibrations.
Another recently developed method utilizes coherent radiation to determine the frequency components of the longitudinal profile. Though coherent radiation has long been studied theoretically [12-13], it was not until 1989 when CSR was first observed experimentally by Nakazato's group at Tohoku University with a linac machine [14]. Since then, coherent radiation has been extensively studied at Tohoku University and Osaka University for various radiation mechanisms [15]. Meanwhile, Coherent Transition Radiation (CTR) was first measured by the Cornell group in 1991 [16].
In general, the total radiation power is the summation
of the power from each individual electron with a phase factor,
and is given in Eq. (1).
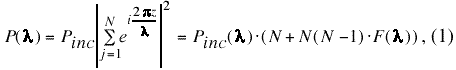 , (1)
, (1)
where ![]() is the radiation power
from an individual electron,
is the radiation power
from an individual electron, ![]() is the number
electrons per bunch, and
is the number
electrons per bunch, and ![]() is the wavelength
of the radiation.
is the wavelength
of the radiation. ![]() is a bunch form factor
given by
is a bunch form factor
given by
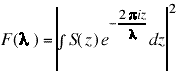 (2)
(2)
where ![]() is the normalized longitudinal
density distribution and the integral is over a single bunch.
The first term on the right side of Eq (1) is the incoherent power
proportional to the number of electrons and the second term is
the coherent power proportional to the square of the number of
electrons. The form factor is nearly zero in regions where the
radiation wavelength is much shorter than the bunch length and
becomes close to one when the wavelength is much longer than the
bunch length. In between is a transition region. This is illustrated
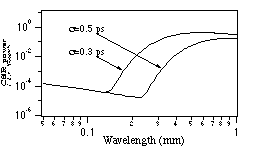
in Fig. 1, where the CSR power spectrum is plotted for bunches
with a Gaussian distribution. The dashed line is the incoherent
term. The coherent enhancement is clearly seen and the location
of the transition region is determined by the bunch length.
is the normalized longitudinal
density distribution and the integral is over a single bunch.
The first term on the right side of Eq (1) is the incoherent power
proportional to the number of electrons and the second term is
the coherent power proportional to the square of the number of
electrons. The form factor is nearly zero in regions where the
radiation wavelength is much shorter than the bunch length and
becomes close to one when the wavelength is much longer than the
bunch length. In between is a transition region. This is illustrated
in Fig. 1, where the CSR power spectrum is plotted for bunches
with a Gaussian distribution. The dashed line is the incoherent
term. The coherent enhancement is clearly seen and the location
of the transition region is determined by the bunch length.
To determine longitudinal profile information, the radiation spectrum needs to be measured over the transition region. Several such measurements have been done at different facilities. Usually, the measurement consists of a radiator, a frequency selecting device, and a detector. Here are a few examples. In 1991, the CSR spectrum was first measured by Ishi at Tohoku University over a wavelength range from 0.16 to 3.5 mm [17]. A bending magnet was used to generate synchrotron radiation, which is commonly used due to its noninvasive nature, a grating-type spectrometer was employed, one of the widely used spectrum measurement devices, and a He-cooled bolometer was chosen as a detector to provide high sensitivity. CTR spectra were measured by Happek at Cornell University in 1991 [16]. An Al foil was inserted to the beam line to produce transition radiation, another widely used radiation mechanism due to its higher power and due to the flatness of the incoherent power spectrum. Wire mesh filters were used to obtain spectral information, and a Golay cell detector was employed due to its flat response. Limited by the wire filters, only five points of the spectrum were obtained. More recently, an autocorrolation measurement, which was proposed by Barry in 1991 [18], was completed by Lihn in 1995 at Stanford University for CTR from much shorter bunches [7]. A Michelson interferometer, another popular device for spectrum measurement, and a pyroelectric detector were used. This frequency-domain technique gives better performance for shorter bunches. However, its main shortcoming is the ambiguity of retrieving the bunch profile from the measured power spectrum, since the measured power spectrum is the square of Fourier transformation of the longitudinal distribution function, and there is no phase information. Using the Kramers-Kronig relations to calculate minimal phases was proposed by Lai [19], which needs to be experimentally verified.
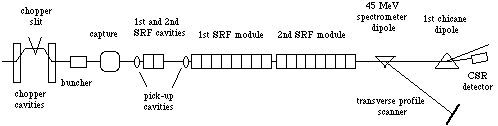
A very stringent demand on final energy spread, with a design goal of 2.5 10-5 (rms), requires short bunches at the Continuous Electron Beam Accelerator (CEBA) of Jefferson Lab [5, 20]. CEBA is routinely operated within its bunch length specification of 0.5 picosecond, and a bunch length as short as 84 fs has been achieved. Three bunch length related measurements have been performed and systematic studies of longitudinal bunching process have been carried out with the assistance of simulation tools. A block diagram of the CEBA injector layout is given in Fig. 2. A 0.1 MeV CW electron beam is chopped by a pair of RF chopper cavities into a bunch train with variable length from 0 to 100 ps separated by 2 ns. The beam is bunched and accelerated to 0.5 MeV by RF buncher and capture cavities. Then the beam is further bunched and accelerated to 5 MeV by the two Superconducting RF (SRF) cavities, followed by 16 SRF cavities to accelerate the beam to the final injection energy of 45 MeV.
A phase transfer function measurement has been proposed
and utilized routinely over the last a few years [21-22]. A relatively
narrow chopper slit is used and the phases of the chopper cavities
are modulated, equivalent to sampling a small portion of the nominal
bunch piece by piece. The arrival phases of the sampled beam are
measured by two longitudinal pick up cavities at strategic locations
down stream, operating at fourth harmonic of operating RF frequency
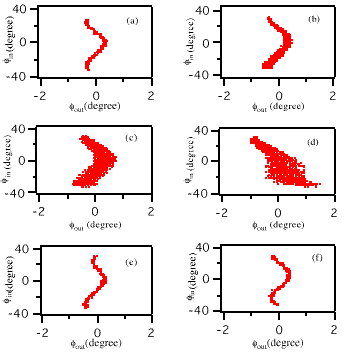
of 1497 MHz. A particular measurement result of a phase transfer
function at the first pick up cavity is shown in Fig. 3(a). Such
measurements can give a time resolution to better than one tenth
of a picosecond. However, since this measurement only quantifies
phase compression, the effects of initial energy spread and space
charge are not determined. Therefore, the profile that can be
obtained from projection of the phase measurement is only valid
for bunches with small initial energy spread and low charge per
bunch. PARMELA simulation results are in good agreement with the
measurements (see Fig. 3(b)), where the initial energy spread
and space charge were turned off. When a significant initial energy
spread and both energy spread and space charge were turned on,
the simulation results shows rather obvious effects (see Fig.
3(c) and (d), respectively). Nevertheless, the measured patterns
of phase provide unique signatures of RF cavity parameters [22].
A distinguishable slope change of the measured pattern results
from a four tenth of degree phase change of the capture cavity
(see Fig. 3(e)) while a vertical slip of the pattern is displayed
(see Fig. 3(f)) due to a two degree change of chopper gang phase.
These pattern recognition techniques have been proven to be invaluable
to operate the machine and are routinely used to correct RF phase
drifts and reproduce RF phases to within a couple of tenths of
a degree.
A zero phasing measurement was employed to measure
bunch length and obtain longitudinal profile information [23-24].
The measurement requires several RF cavities (zero-phasing cavities),
a spectrometer, and a transverse profile measuring device. The
RF cavities operated at zero-crossing of the accelerating gradient
impart a time correlated momentum tilt along the beam bunch. Then
the spectrometer translates the longitudinal momentum spread into
a horizontal position spread. By measuring the horizontal profile,
the bunch length and longitudinal profile can be determined. Nominally,
16 SRF cavities in the first and second SRF modules are running
on crest to achieve maximum energy gain and minimum energy spread.
During the measurement, the last 8 SRF cavities are phased to
90 degree off crest. A wire scanner is used to measure horizontal
profile at spectrometer. The relation between the bunch length
and the transverse beam width at the scanner is given in Eq. (3),
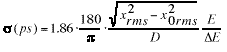 (3)
(3)
where ![]() is the rms bunch length,
1.86 is unit conversion factor between RF degrees and ps,
is the rms bunch length,
1.86 is unit conversion factor between RF degrees and ps, ![]() is the dispersion of the spectrometer,
is the dispersion of the spectrometer, ![]() is beam energy with the zero-crossing cavities off,
is beam energy with the zero-crossing cavities off, ![]() is the energy gain at crest of the zero-crossing cavities, and
is the energy gain at crest of the zero-crossing cavities, and
![]() and
and ![]() are horizontal
rms widths at the scanner with the zero-crossing cavities on and
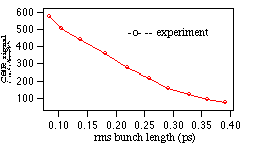
off, respectively. This relation and measurement procedure were
tested using a simulation where the zero-phasing measurement is
performed and compared to the actual bunch length. The results
shows good agreement over bunch length of 0.1 to 0.4 ps range
except a 10 fs offset.
are horizontal
rms widths at the scanner with the zero-crossing cavities on and
off, respectively. This relation and measurement procedure were
tested using a simulation where the zero-phasing measurement is
performed and compared to the actual bunch length. The results
shows good agreement over bunch length of 0.1 to 0.4 ps range
except a 10 fs offset.
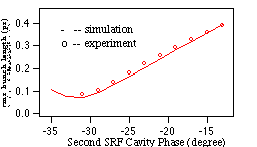
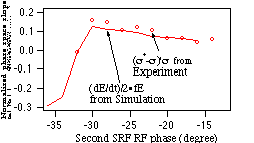
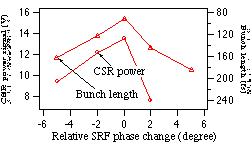
The bunch length was systematically changed by varying
the second SRF cavity phase, resulting in longitudinal phase space
rotations. Excellent agreement has been achieved between the measurement
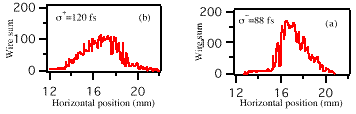
and simulation, shown in Fig. 4. It was observed that plus and
minus 90 degree off the crest gave different measured bunch lengths,
as shown in Fig. 5a and b, which is also consistent with the simulation
results. The reason is that in general, the longitudinal phase
space ellipse of the incident beam has a slope, dE/dt. The RF
wave has slope of +/- 2'fÆE at the zero-crossings. When
these two slopes have the same sign, the measured horizontal profile
will be wider, giving a longer bunch length. Therefore, the average
bunch length of the two should be used. A relation between the
phase space slope and measured bunch length is found to be
![]() (4)
(4)
where ![]() are the measured bunch
length with zero-phasing cavities at plus and minus 90 degree
off crest, respectively, and
are the measured bunch
length with zero-phasing cavities at plus and minus 90 degree
off crest, respectively, and ![]() is the average.
The left side of Eq (4) is plotted from simulation in the solid
line while the right side of Eq (4) is displayed from measurement
in circles in Fig. 6, as the phase of the second SRF bunching
cavity is varied. They agree pretty well. It is noted that the
zero value point represents the upright position of the ellipse
in the phase space, where the shortest bunch was obtained in both
experiment and simulation. There is a steep slope around the zero
point where the slope of the ellipse changes sign, corresponding
to the transition from under compression to over compression.
The zero phasing measurement gives bunch length with high precision.
The main shortcomings are that the measurement is destructive
and time consuming.
is the average.
The left side of Eq (4) is plotted from simulation in the solid
line while the right side of Eq (4) is displayed from measurement
in circles in Fig. 6, as the phase of the second SRF bunching
cavity is varied. They agree pretty well. It is noted that the
zero value point represents the upright position of the ellipse
in the phase space, where the shortest bunch was obtained in both
experiment and simulation. There is a steep slope around the zero
point where the slope of the ellipse changes sign, corresponding
to the transition from under compression to over compression.
The zero phasing measurement gives bunch length with high precision.
The main shortcomings are that the measurement is destructive
and time consuming.
To combat the shortcomings of the previous methods,
a noninvasive CSR bunch length monitor has been developed [25-27].
Comparing two CSR power spectrum curves in Fig. 1, the spectrum
for the shorter bunch length covers the spectrum for the longer
bunch length at long wavelengths, but has extra power at short
wavelengths. Therefore, the output signal from a CSR power detector
with an arbitrary "bandpass" characteristic will always
increase as the bunch length becomes shorter, until such power
changes take place at wavelengths outside the range of the detector.
Such a monitor was installed after the first chicane dipole. The
key component of the detector is a state-of-the-art whisker contacted
GaAs Schottky diode developed and fabricated at the Semiconductor
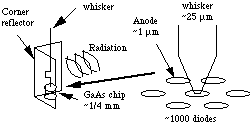
Device Lab of the University of Virginia [28-30]. The diode assembly
, shown in Fig. 7, consists of a 1/4 mm GaAs chip, a 90 degree
polished corner reflector, and a 1 mil whisker wire. The whisker
acts as a four wavelength traveling wave antenna with a 90 degree
bend inductively cutting off the induced current to the open end.
Its tip is etched to less than 1 ![]() and contacts
one of thousands of 1
and contacts
one of thousands of 1 ![]() "honey-comb"
Schottky diodes on the chip (see the right side of the drawing).
The corner reflector is introduced to sharpen radiation pattern
around the antenna. The radiation is focused on to the diode by
a parabolic reflector following a single crystal quartz vacuum
window. The diode is connected to a DC current supply providing
a typical 1
"honey-comb"
Schottky diodes on the chip (see the right side of the drawing).
The corner reflector is introduced to sharpen radiation pattern
around the antenna. The radiation is focused on to the diode by
a parabolic reflector following a single crystal quartz vacuum
window. The diode is connected to a DC current supply providing
a typical 1 ![]() operating current. Due to
its nonlinear properties, a small voltage change, proportional
to the incident radiation power, is generated and can be measured
as the CSR signal. The diodes have high sensitivity. Unlike thermal
detectors, due to its antenna structure the diode is insensitive
to the background black body type radiation. The bandpass feature
also makes it less responsive to background radiation outside
of the interesting wavelengths. CSR signals were measured (see
Fig. 8) and calibrated by the zero-phasing measurement shown above.
The bunch length as short as 84 fs or 25
operating current. Due to
its nonlinear properties, a small voltage change, proportional
to the incident radiation power, is generated and can be measured
as the CSR signal. The diodes have high sensitivity. Unlike thermal
detectors, due to its antenna structure the diode is insensitive
to the background black body type radiation. The bandpass feature
also makes it less responsive to background radiation outside
of the interesting wavelengths. CSR signals were measured (see
Fig. 8) and calibrated by the zero-phasing measurement shown above.
The bunch length as short as 84 fs or 25 ![]() was achieved, and found simply by peaking the CSR signal (see
Fig. 9). The measurement was done with a 513
was achieved, and found simply by peaking the CSR signal (see
Fig. 9). The measurement was done with a 513 ![]() diode plus a 20% bandpass mesh filter [31], for 3x105
electrons per bunch. With 200 sample average, the CSR signals
after amplification have a signal to noise ratio of 450 for the
84 fs bunch and 100 for a bunch length of 0.6 ps. The main limitation
on the resolution in our experiment is due to a slow signal fluctuation
of about 30 mV with a few minute time scale. At typical operating
conditions, the CSR signal changed from 4 V to 2 V as the bunch
length increased from 0.45 ps to 0.6 ps, so a bunch length change
of a few fs may be resolved for Gaussian bunches. The monitor
is noninvasive and has high resolution. It is also compact (3
cm in size), relatively inexpensive (a few thousand US dollars),
and operates at room temperature. Potentially such a monitor can
be integrated into a feedback of a control system to lock the
operating bunch length. Its main shortcoming is that it can not
provide an absolute value of bunch length. Therefore, it needs
to be calibrated with a precise bunch length measurement such
as the zero-phasing [26-27].
diode plus a 20% bandpass mesh filter [31], for 3x105
electrons per bunch. With 200 sample average, the CSR signals
after amplification have a signal to noise ratio of 450 for the
84 fs bunch and 100 for a bunch length of 0.6 ps. The main limitation
on the resolution in our experiment is due to a slow signal fluctuation
of about 30 mV with a few minute time scale. At typical operating
conditions, the CSR signal changed from 4 V to 2 V as the bunch
length increased from 0.45 ps to 0.6 ps, so a bunch length change
of a few fs may be resolved for Gaussian bunches. The monitor
is noninvasive and has high resolution. It is also compact (3
cm in size), relatively inexpensive (a few thousand US dollars),
and operates at room temperature. Potentially such a monitor can
be integrated into a feedback of a control system to lock the
operating bunch length. Its main shortcoming is that it can not
provide an absolute value of bunch length. Therefore, it needs
to be calibrated with a precise bunch length measurement such
as the zero-phasing [26-27].
The strategy of bunch length control at Jefferson
Lab is: use zero-phasing measurements as the primary standard
to characterize the longitudinal beam dynamics and calibrate the
CSR monitor with the assistance of PARMELA simulations as cross-checks,
use the CSR detector to monitor bunch length during beam delivery,
and when the CSR signal varies outside of acceptable bounds indicating
the bunch length has changed, use the phase transfer function
measurement to correct the RF phase drifts that have occurred.
Several bunch length related measurement in the subpicosecond parameter regime have been discussed. The conventional streak camera or fast deflecting cavity can be employed in the subpicosecond regime with some significant capital investment and operating expertise. Coherent radiation detection techniques offer a very attractive alternative, which is relatively easy to operate, much less expensive, and has excellent performance for shorter bunches. The uncertainty of extracting the longitudinal profile from measured power spectrum needs to be experimentally resolved.
At Jefferson Lab, a phase transfer function measurement
is used to correct and reproduce RF phases to a couple tenths
of degree, which is easy to implement and gives high sensitivity.
The zero-phasing method was employed to characterize the bunching
process; bunch lengths as short as 84 fs have been measured. Excellent
agreement has been achieved between experiment and simulation,
and simulation has been very helpful in understanding the measurement
results. A noninvasive CSR bunch length monitor using a Schottky
diode has been developed. The diode provides very high sensitivity,
which means it is able to detect bunch length changes of order
1 fs and for charges as low as 105, per
bunch at a bunch length of 0.5 ps. It is compact, inexpensive,
and operated at room temperature. The shortest bunch was found
experimentally by peaking the CSR signal from the diode.
The author gratefully acknowledges G. A. Krafft,
P. Wood, D. Porterfield, and T. Crowe for their contribution to
the work done at Jefferson Lab. He would like to thank H. Nguyen,
R. Abbott, and E. Feldl for their excellent technical support,
and CEBA operations personnel for their help on the measurement.
He wants to thank B. Dunham and H. Liu for their help on running
PARMELA simulation code. He would also like to thank C. Sinclair
for his constant encouragement and support. This work was supported
by U.S. DOE under contract #DE-AC05-84ER40150.
[1] H. Winick, et al., NIM, A347 (1994), 199.
[2] R. H. Sieman, Proc. of 1993 PAC Conf., 532.
[3] W. B. Mori, et at., AIP Conf. Proc. 335, 112 (1994).
[4] T. Raubenheimer, et al., Proc. of 1993 PAC Conf., 635.
[5] G. A. Krafft, Proc. of 1994 LINAC Conf., 9.
[6] B. Carlsten, AIP Conf. Proc. 367, 21 (1995).
[7] H. C. Lihn, et al., Phys. Rev. E53, 6413 (1996).
[8] D. X. Wang, et al., submitted to Appl. Phys. Lett.
[9] M. Uesaka, et al., Phys. Rev. E 50, 3068 (1994).
[10] L. Farvacque, et al., AIP Conf. Proc. 367, 245 (1995).
[11] A. Lumpkin, AIP Conf. Proc. 367, 327 (1995).
[12] J. S. Nodvick, et al., Phys. Rev. 96, 180 (1945).
[13] F. C. Michel, Phys. Rev. Lett. 48, 580 (1982).
[14] T. Nakazato, et al.., Phys. Rev. Lett. 63, 1245 (1989).
[15] T. Nakazato, et al., AIP Conf. Proc. 367, 307 (1995).
[16] U. Happek, et al., Phys. Rev. Lett. 66, 1967 (1991).
[17] K. Ishi, et al., Phys. Rev. A43, 5597 (1991).
[18] W. Barry, Proc. of Workshop on Advanced Beam Instrumentation, KEK, Tsukuba, Japan (1991).
[19] R. Lai, et al., Phys. Rev. E 50, 4294 (1994).
[20] B. Dunham, these proceedings.
[21] C. G. Yao, AIP Conf. Proc. 229, 254 (1992).
[22] G. A. Krafft, AIP Conf. Proc. 367, 46 (1995).
[23] G. Mavrogenes, et al., Proc. of 11th Int. Conf. on High-Energy Accl., 481 (1980), and R. Miller private communications (1995).
[24] K. Bane, SLAC-PUB-5177 (1990).
[25] E. Price, CEBAF TN-93-077 (1993).
[26] G. A. Krafft, et al. Proc. of 1995 PAC Conf., 2601.
[27] D. X. Wang, et al., AIP Conf. Proc. 367, 502 (1995).
[28] T. W. Crowe, et al., Proc. IEEE, 80, 11 (1992).
[29] W. Peatman, et al., Int. J. of Infrared and Millimeter Waves, 11 (3), 355 (1990).
[30] P. Wood, PhD Thesis, University of Virginia (1994).
[31] D. Porterfield, et al., Appl. Optics, 33 (25), 6046 (1994).