A 432-MHz, 3-MeV radio-frequency quadrupole (RFQ) linac was developed for the Japanese Hadron Project (JHP). This four vane-type RFQ was stabilized against the dipole-mode mixing with newly devised ¹-mode stabilizing loops (PISLs). In order to inject a low-emittance H- beam into the RFQ, a newly designed pre-injector composed with a volume production H- ion source (VPIS) and a low-energy beam transport (LEBT) has been developed. A H- beam of 16 mA with a 90% normalized emittance of 0.41¹ mm·mrad was produced by the VPIS operated without cesium and injected within the design acceptance of the RFQ. The RFQ accelerated 13.2 mA of the beam with a transmission efficiency of 82.5%.
A radio-frequency quadrupole (RFQ) linac was developed for the Japanese Hadron Project (JHP) [1]. The design values of its resonant frequency, duty factor, peak beam current, injection and final energies were determined from a beam-optics consideration of the entire system to be 432 MHz, 3% (600 µs × 50 Hz), 20 mA, 50 keV and 3 MeV, respectively [2].
Since the final energy is rather higher than common RFQs, the optimization of the beam dynamics design is important to minimize the cavity length, which relates with not only the acceleration efficiency but also the field errors and stability. Therefore, we developed a new design procedure in order to optimize the design of intermediate- or high-beam current RFQs, which is programmed in the computer code package KEKRFQ [4]. By using KEKRFQ, we succeeded in designing the RFQ with a relatively short length of 2.7 m for such a high-energy RFQ. For the stable operation with a high-duty factor of 3%, newly devised ¹-mode stabilizing loops (PISLs) were installed into this four-vane type RFQ in order to stabilize the field against the dipole-mode mixing due to the thermal deformation [5,6]. PISL has the following two advantages compared with vane coupling ring (VCR ) [7], which is the similar field stabilizer as PISL and has been used frequently so far; (1) much easier water-cooling and (2) more uniform longitudinal electric field distribution [8,9]. By installing several pairs of PISLs to the RFQ, we obtained a uniform field distribution within ±0.75% both azimuthally and longitudinally [10]. Also for the stable operation with a negligible probability of the intervane discharge, the maximum surface electric-field was kept smaller than 1.8 times of Kilpatric limit. In order to keep this restriction without reducing the acceleration efficiency, the pole-tip of each vane was cut by a rotating concave cutter into the cross-section with a curvature of 75% of the average bore radius [11]. This machining method is called as two-dimensional cutting (2DC). Since the machine setting in 2DC is easier than in three-dimensional cutting (3DC), we succeeded in constructing the RFQ with a small intervane distance errors of ±20 µm [12]. In order to correct the energy gain of each cell to the value produced in the ideal vane shape, each cell was machined with a slightly larger modulation factor according to Ref. [11].
In the preliminary beam test of the RFQ using a multi-cusp proton ion source and an Einzel lens, we experienced the difficulty to operate the high-voltage electrostatic lens stably with a high-duty factor. Therefore, we studied various low energy beam transports (LEBTs) using several types of magnetic lenses by simulating the beam optics with a computer code BEAMPATH [13,14]. By these studies, it was revealed that an appropriately designed solenoid magnet had the smallest lens aberration. Consequently, we succeeded in designing the LEBT without any practical emittance growth due to the lens aberration by using two short and strong solenoid magnets. We also studied how to align the permanent magnets around the arc chamber of a volume production H- ion source (VPIS) by calculating three-dimensional magnetic field distribution, in order to increase the plasma confinement efficiency. We constructed thus designed pre-injector composed with the VPIS and the LEBT in order to inject a low-emittance H- beam within the design acceptance of the RFQ.
In this paper, we represent the results of the beam test of the pre-injector and the RFQ. The detailed results of the beam test in the LEBT including the space-charge neutralization effects and the comparison of the measured results with the simulation are described in Ref. [15].
At first, the experimental setup is described in drawings.
A schematic drawing of the VPIS and the LEBT viewing from the upper position is shown in Fig. 1. In the VPIS, we use three types of permanent magnets; (1) the permanent magnet for plasma confinement (PM), (2) the permanent magnet for magnetic filter (PMMF) and (3) the permanent magnet for electron suppression (PMES) installed inside of the extraction electrode (EE). Six pairs of PMs, one pair of PMMFs and one pair of PMESs are aligned symmetrically with the vertical plane including the beam axis. Each PM or PMMF is a semicircle around the beam axis. Each PMES is a rod with a length of 40 mm aligned parallel to the symmetric plane. The sizes of the cross sections of PM, PMMF and PMES (width × height) are 8 mm ×16 mm, 10 mm × 20 mm and 5 mm ¥ 3 mm, respectively. Since PMESs bend the electrons extracted from AC and hit almost all of them to EE, PMESs are made of Sm-Co material with a high Curie temperature in order to avoid their demagnetization due to the heat transferred from the electrons. On the other hand, PMs and PMMFs are made of Nd-Fe-B material. Each PM, PMMF or PMES is magnetized normal or anti-normal to the surface of the arc chamber. The paired two PMs, PMMFs or PMESs has different magnetization direction. The neighboring two PM or PMMF has also different magnetization direction. However, the neighboring PMMF and PMES has same magnetization direction. The arc chamber (AC) with a inner diameter of 150 mm and a inner length of 150 mm is made of copper. The plasma electrode (PE) with a tapered hole of a diameter from 7 to 9 mm is made of Mo plate with a thickness of 2 mm. AC and PE are electrically isolated by separating with a ceramics plate. The bias voltage (Vb) is fed between AC and PE. We use a LaB6 filament (FL; DENKA beta plus C-9a) with a diameter of 15 mm and a length of 32 mm. Arc pulse voltage is fed between FL and AC. A tapered hole of a diameter from 6 to 10 mm is bored on EE made of a copper plate with a 10 mm thickness. The extraction voltage is fed between PE and EE. The gap between PE and EE is 3 mm. The ground electrode (GE) with a hole of a diameter of 12 mm is made of stainless plate with a thickness of 5 mm. The acceleration voltage is fed between EE and GE. The gap between EE and GE is 20 mm. In order to correct the beam angle due to the dipole magnetic field produced by PMMF and PMES, the steering electromagnet (STM) with a pole length of 10 mm is located 21 mm downstream from GE. The vacuum chamber just after the VPIS (CHM1) is pumped out with two 1500 l/s turbo molecular pumps (1500TMPs). The first solenoid electromagnet (SM1) is located 20 mm downstream from STM. In a space of 215 mm between SM1 and the second solenoid electromagnet (SM2), the vacuum chamber for the beam monitor (CHM2) and the gate valve (GV) are located. SM1 and SM2 have the same shape with a length of 100 mm, a outer diameter of 300 mm and a bore diameter of 50 mm. A 500 l/s turbo molecular pump (500TMP) pumps out CHM2. The movable Faraday-cup (MFC) is used to measure the total beam intensity extracted from VPIS. Since MFC is connected to the ground through 50-½ resistance, we can measure the intensity by measuring the induced voltage on the resistance (20 mA/V). By moving the movable slit (EMSLLH) and the Faraday-cup with slit (EMFCLH) horizontally step by step, the horizontal emittance is measured. The vertical emittance is measured by using EMSLLV and EMFCLV. The steps of x (y) and x' (y') were 0.2 mm and 2 mrad, respectively. Each slit used in EMSLL or EMFCL is made of molybdenum plates with a thickness of 0.05 mm and has a gap of 0.2 mm. The distance between the slit of EMSLL and the slit of EMFCL is 61 mm. A voltage of -1 kV was fed on each bias electrode of MFC or EMFCL in order to suppress the secondary electrons form each Faraday-cup. The distance between SM2 and the vane end at the entrance of the RFQ is 35 mm.
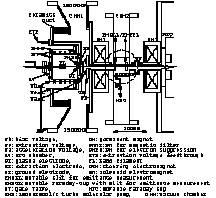

A schematic drawing of the diagnostic devices for the beam ejected from the RFQ (DRFQ) viewing from the upper position is shown in Fig. 2. In order to focus the beam, two quadrupole-magnets (QF and QD) are used. The distance between the vane-end at the exit of the RFQ and the pole of QF is 90 mm. The pole lengths of QF and QD are 60 and 50 mm, respectively. In a space of 118 mm between QF and QD, the gate valve (GV) is located. The energy analyzing magnet (AM) with a pole length of 90 mm is located 182 mm downstream from QD. Tow pairs of the movable slit and the movable Faraday-cup with slit (EMSLDH and EMFCDH for the horizontal emittance and EMSLDV and EMFCDV for the vertical emittance) are used in order to measure the transverse emittances. The steps of x (y) and x' (y') were 0.2 mm and 0.5 mrad, respectively. The distances between AM and EMSLD and between EMSLD and the slit of EMFCD are 93 mm and 205 mm, respectively. Each slit used in EMSLD or EMFCD is made of aluminum plates with a thickness of 0.1 mm and has a gap of 0.2 mm. The total beam intensity is measured with Faraday-cup FC1. The beam intensity accelerated up to 3 MeV is measured with Faraday-cup FC2, when the coil current of AM is 57.5 A (BL = 0.00483 T·m). FC1 and FC2 are also connected to the ground through 50-½ resistances as same as MFC. A voltage of -1 kV was fed on each bias electrode of FC1, FC2 or EMFCD in order to suppress the secondary electrons form each Faraday-cup.
The typical parameters of the operating VPIS, LEBT and RFQ are summarized in Table 1. At present, the duty of the operation of the VPIS is limited by the performance of the arc power supply. The second trace of Fig. 3 shows the VPIS beam signal measured with MFC. Since the vertical scale is 10 mA/Div., the peak intensity is 16.0 mA. When both of the coil currents for STM and SM1 was set to 0 A, the intensity measured with MFC was 16.5 mA. Therefore, the electron current accelerated up to 50 keV was 0.5 mA. The signal of the beam accelerated with the RFQ and analyzed with AM were measured with FC2 as shown in the top trace of Fig. 3. Since 13.2 mA of the injected beam of 16.0 mA was accelerated, the transmission efficiency was 82.5%. The third and bottom traces of Fig. 3 show the arc pulse voltage (125 V/Div.) and arc pulse current (50 A/Div.), respectively. The peak arc power is calculated to be 170 V × 220 A = 37.4 kW.
| VPIS: | Filament Voltage | 8.9 V (Filament Current 69 A) |
| Arc Current | 220 A (Arc Voltage 170 V) | |
| Bias Voltage | 12.4 V Extraction Voltage 7.0 kV | |
| Acceleration Voltage | 43 kV | |
| H2 gas flow | 8.6 CCM | |
| Arc pulse duty | 0.7% (350 µs × 20 Hz) | |
| LEBT: | Vacuum pressure of CHM1 | 1.8 × 10-5 Torr |
| Vacuum pressure of CHM2 | 3.7 × 10-6 Torr | |
| Current of STM | 3.0 A (120A T, 167G cm) | |
| Current of SM1 | 325 A (45500A T) | |
| Current of SM2 | 420 A (58800A T) | |
| RFQ: | RF power | 480 kW for design intervane voltage |
| RF duty | 0.4% (215 µs × 20 Hz) | |
| Vacuum pressure | 1.2 ×10-7 Torr (rf on, beam on)
7.3 ×10-8 Torr (rf on, beam off) 1.3 ×10-8 Torr (rf off, beam on) 5.3 ×10-8 Torr (rf off, beam off) |
In Figures 4(a), 4(b), 5(a), 5(b), 6(a) and 6(b), the measured
particle distributions in the emittance phase planes are shown.
Instead of the commonly used contour plot, we used a new display
method of Ueno-Fujimura plot (UF-plt, see Appendix A). As described
in Appendix A, the detailed structure of the distribution can
be shown with UF-plt. Figures 4(c), 4(d), 5(a), 5(b), 6(a) and
6(b) shows the relationships between emittance and the beam fraction
contained in the emittance. Here, the suffixes of (a) and (c)
are used for the results of the horizontal emittance measurements
and (b) and (d) are used for those of the vertical emittance measurements.
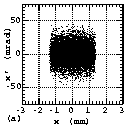
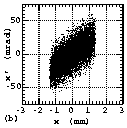
Figures 4, 5 and 6 show the results measured at EMSLL position
in the LEBT, at the entrance of the RFQ and at EMSLD position
in the DRFQ, respectively. The results shown in Figs. 5 and 6
are measured with the parameters shown Table 1. The results shown
in Fig. 4 was measured by setting both of the currents of STM
and SM1 to 0 A in order to measure the pure characteristics of
the VPIS beam with out any unexpected affects, for example, the
interference between STM and SM1 and so on. Therefore, an electron
current of 0.5 mA are included in the distributions as described
above. As can be seen from the figures with suffixes of (c) and
(d), the 90% normalized emittances at EMSLL position, the RFQ
entrance and EMSLD position were about 0.66, 0.41 and 0.55¹
mm·mrad, respectively. Because of the contained electrons
in the distributions measured at EMSLL, the 90% normalized emittances
seem to have larger values than those at the entrance of the RFQ.
The 90% normalized emittances grew during the acceleration in
the RFQ by 34%. Since there is almost no filamentation in Fig.
4(a), the small filamentation in Fig. 4(b) seem to be caused by
the magnetic field generated with PMESs. If the electric fields
produced by the extraction and acceleration voltages caused the
filamentation, both of the distributions should suffer the same
affects. Since the filamentations are measured in Figs. 5(b) and
6(b), the filamentation seems to be transferred from the horizontal
emittance to the vertical emittance by the rotation effect of
the solenoid magnetic field.

We compared the beam profile measured at the entrance of the RFQ, which was generated by projecting the distribution in Fig. 5(a) onto the real axis (x), with the simulation results using the KV-distribution, Gaussian-distribution and Ueno-Yokoya distribution (UY-dst, see Appendix B) as the initial particle distributions at the exit of the VPIS. As described in Appendix B, UY-dst has understandable physical meanings; the uniform distribution in the real space led from the uniform plasma density and the gaussian distributions of x' and y' led from the thermal motion of the plasma. As shown in Fig. 7, the distribution in the real space simulated with UY-dst showed good agreement with the measured beam profile.
We measured the dependence of the accelerated beam intensity on the normalized intervane voltage (Fig. 8). Since the beam was increased by only 4% with the 12% higher intervane voltage than the design value, the H- beam seemds to be lost due to the electron stripping by the collision with the following out gas in the RFQ cavity. (If the acceptance of the RFQ reduced the transmission, the lager improvement of the intensity by the higher intervane voltage was expected.) During about 150 µs after the start of the beam ejection from the VPIS, there was no rf excitation in the RFQ due to the delay of the klystron. The large amount of out gas produced by the collision of the H- beam with the cavity wall should be localized around the entrance of the RFQ.
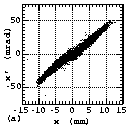
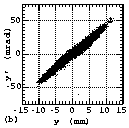
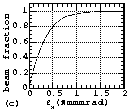
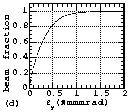
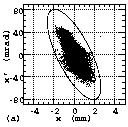
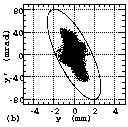
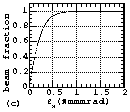
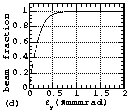
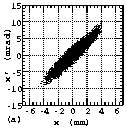
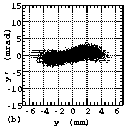
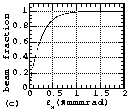
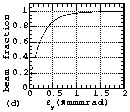
Fig. 6 The measured particle distributions in emittance phase
planes (a and b) and the relationships between emittance and the
beam fraction contained in it (c and d) measured at EMSLD position.
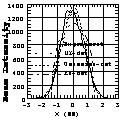 | 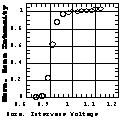 |
| Fig. 7 The particle distribution in the real space (y) measured at the entrance of the RFQ, which is compared with simulated results with the initial distributions of Gaussian, KV and UY. | Fig. 8 The relationship between the intervane voltage normalized with the design value and the beam intensity accelerated by the RFQ normalized with the intensity accelerated with the design intervane voltage. |
When a beam of 13.2 mA were accelerated with the RFQ, the input rf power should be increase by around 40 kW in order to keep the design rf level in the RFQ. The estimated beam current from the beam loading of I = 40 kW/(3000-50) kV = 13.6 mA showed good agreement with the beam current of 13.2 mA deteced with FC2.
We succeeded in extracting a H- beam of 16 mA from a newly developed volume production H- ion source operated without cesium and injecting it within the design acceptance of the JHP RFQ by using the LEBT with two short and strong solenoid magnets. Although the 90% normalized emittance (0.41¹ mm·mrad) measured at the entrance of the RFQ was about two-fifth of the design acceptance of the RFQ, the transmission efficiency of 82.5% is rather smaller than the value of 94% simulated with PARMTEQ [16]. Since the PARMTEQ installed at KEK simulates the beam optics by using the ideal quadrupole electric field and neglecting the effects of the image-charges, the possible causes for this discrepancy are as follows; (1) the electron stripping by the collision with the out gas produced by the lost H- struck on the cavity wall, (2) the higher-order components of the electric field generated by the shape of the vane-tip machined with two-dimensional cutting and (3) the effects of the image-charge induced on the vane-tip by the beam itself.
The measured 90% normalized emittance of the beam accelerated with the RFQ was 0.55¹ mm·mrad. The emittance grawth ratio during the acceleration by the RFQ was 34%.
Since the JHP RFQ has the excellent field uniformity and field stability produced by the field stabilizer PISL, the measured trsnsmissition effficiency (82.5%) and the emittance growth ratio (34%) will be explained by the simulations, in which the vane-tip shape effects and the image charge effects are taken into account, and the futher experiment on the vacuum presuure effects in the RFQ cavity. The arc pulse power suplly will be modified for the operation with a design duty factor of 3.5%. The plasma confinement efficiency of the arc chamber will be also improved furthermore for a higher beam intensity.
The authors wish to express their sincere thanks to Mr. Kazuyuki Suzuki and the other members of the Accelerator System Design Section and the Tools Section at Hitachi Works, Hitachi, Ltd. for their technical support.
[1] Y. Yamazaki and M. Kihara, Proc. 1990 Lin. Accel. Conf., LANL report, LA-12004-C, 543, (1991).
[2] A. Uneo et al., Proc. 1994 Linear Accelerator Conf., 166, (1994).
[3] A. Uneo et al., Proc. 1994 Linear Accelerator Conf., 169, (1994).
[4] A. Ueno and Y. Yamazaki, Proc. 1990 Lin. Accel. Conf., LANL report, LA-12004-C, 329, (1991).
[5] A. Ueno and Y. Yamazaki, Nucl. Instr. and Meth. A300, 15, (1991).
[6] A. Ueno, T. Kato and Y. Yamazaki, Proc. 1990 Lin. Accel. Conf., LANL report, LA-12004-C, 57, (1991).
[7] H.R. Schneider and H. Lancaster, IEEE Trans. Nucl. Sci., NS-30, (4),3007, (1983).
[8] A. Ueno et al., Proc. 1992 Linear Accelerator Conf., AECL report, AECL-10, 728, (1992).
[9] F.O. Purser et al., Proc. 1984 Linear Accelerator Conf., 115, (1984).
[10] A. Ueno and Y. Yamazaki, Proc. 1994 Linear Accelerator Conf., 172, (1994).
[11] K.R. Crandall, LANL report, LA-9695-MS, (1983).
[12] A. Ueno et al., Proc. 1990 Linear Accelerator Conf., LANL report, LA-12004-C, 60, (1991) .
[13] Y. Batygin, Proc. of EPAC92, Berlin, Vol. 1, 822, (1992).
[14] S. Fujimura, A. Ueno and Y. Yamazaki, Proc. 9th Symp. on Accel. Sci. and Tech., JAERI-Conf 95-021, 254, (1993).
[15] S. Fujimura and A.Ueno, "Measurement of Precise Particle Distributions in Emittance Phase Plane in the JHP LEBT", in this conference.
[16] K.R. Crandall and T. P. Wangler, AIP Conf. Proc. 177, 22 (1988).
[17] K. Yokoya, private communication.
The measured particle distribution in the emittance phase plane
has been commonly displayed with contour plot, so far. However,
the small components of the distribution is easily neglected with
the contour plot, since the number of the contour lines is limited
to less than around 20 due to the resolution of the graphics.
Therefore, we propose a new method of Ueno-Fujimura plot (UF-plt)
in order to display the detailed stractures of the distribution,
for example the filamentation due to the lens-aberration or the
non-linear space charge force. When the emittance measurements
was performed in the range from (x, x') = (-0.4,-4) to (0.4,4)
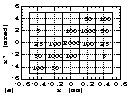
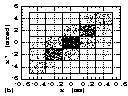
with the steps of dx = 0.2 and dx' = 2, an example of the beam
intensity distribution detected with the emittance monitor can
be shown in the way of Fig. 9(a). Here, the measured beam intensity
at each (x,x') is shown by the numerical figure, for example 2000
at (0,0), and so on. In this measurement, each intensity represents
each small rectangle composed with the four points of (x-dx/2,
x'-dx'/2), (x+dx/2, x'-dx'/2), (x-dx/2, x'+dx'/2) and (x+dx/2,
x'+dx'/2). In UF-plt, the particle distribution is displayed by
plotting points, whose number is propotional to the measured intensity,
randomly within each rectangle as shown in Fig. 9(b). As can be
seen from the figure, it is possible to recognize the components
with a very small intensity of about three-order smaller than
the peak intensity. It is also noted that UF-plt is directly compared
with the results of the simulation using the same number of particles.
As described in the primer text of the accelerator physics,
the shape of the particle distribution in the emittance phase
plane at the exit of the ion source is not ellipse, except for
all of four variables (x, x', y and y') are distributed in Gaussian
way. The Gaussian ditribution of x' and y' has a reasonable physical
meaning, since the origin of the distribution of x' and y' is
the thermal motion of the plasma. However, the Gaussian distribution
in the real space (concering with x and y) is not understandable,
since the plasma should be distributed uniformly around the very
small hole on the plasma electrod. Therefore, we propose a new
distribution of UY-dst as a most realisticdistribution. UY-dst
is generated with the following procedure; (1) the generation
of the random distribution of x and y within a circle of a radius
r, (2) the generation of the Gaussian distribution of x' and y'
by using the probability distribution function of exp{-(x'2+y'2)/2s2}/
sqrt(2¹)/s, (3) focus (defocus) with a thin-lens in order
to reflect the shape of the plasma surface bu using the equations
of x' = x'0+x/f and y' = y'0+y/f and (4) iterrations from
(1) to (3) by changing three parameters of r, s and f in order
to match a, b and e of the rms emittance to the design values
or the measured values. Tow examples of UY-dst are shown in Fig.
10. It is noted that the outward form of each distribution is
a lozenge.