Due to the progress of accelerator technology in recent years it is now possible to consider the construction of a Free Electron Laser (FEL) that provides coherent radiation at wavelengths very far below the visible. In this paper, various projects are mentioned which are under way to establish the Self-Amplified Spontaneous Emission (SASE) principle at very short photon wavelengths as well as multiple harmonic generation. The basic principles are briefly explained and the expected performance is discussed.

With respect to linac technology, the key prerequisite for such single-pass, high-gain FELs is a high intensity, diffraction limited, electron beam to be generated and accelerated without degradation. Key components are RF guns with photocathodes, bunch compressors, and related diagnostics.

Once proven in the micrometer to nanometer regime, the SASE FEL scheme is considered applicable down to Angstrom wavelengths. It is pointed out that this latter option is particularly of interest in context with the construction of a linear collider, which requires very similar beam parameters.

In a Free Electron Laser (FEL), an electron beam radiates photons at much higher power and better coherence than it does due to spontaneous synchrotron radiation. The main idea is that electrons moving in a transverse magnetic field of alternating polarity (undulator) may amplify an existing electromagnetic radiation field (see e.g. [1]). The reason is that for properly chosen phase and wavelength the scalar product of the electron's velocity vector and the electric field vector does not vanish on average, resulting in an average energy transfer between the electron beam and the radiation field. As a consequence of this interaction, depending on the relative phase, some electrons get accelerated and others decelerated. This results in a longitudinal density modulation of the electron beam at the optical wavelength during the passage through the undulator. This, in turn, causes increased, stimulated emission at the resonant wavelength (high gain mode). The radiation power increases exponentially until, mainly because the electrons run out of resonance due to their energy loss, a saturation effect sets in. Compared to state-of-the-art synchrotron radiation sources, one expects better coherence, larger average brilliance, and, in particular, up to eight or more orders of magnitude larger peak brilliance at a pulse lengths of about 200 fs FWHM (see Fig. 3).

Meanwhile many FELs are under operation worldwide, several of them serving as user facilities (for an overview see Ref. [2]). Most of them are operated in the so-called oscillator mode, i.e. the radiation field is accumulated inside an optical cavity formed by two mirrors placed at the entrance and at the exit of the undulator. The major energy transfer from the electron beam to the radiation field takes place only after several electron bunches have passed the optical cavity thus generating an intense radiation field. Such operation principle only needs quite short undulator magnets and moderate values of electron beam parameters like emittance and peak current.

It is an essential advantage of the FEL principle that there is no fundamental limit in the choice of the photon wavelength. The photon wavelength _ph of the first harmonic is related to the period length of a planar undulator _u by

, (1)

where = E/mc² is the relativistic factor of the electrons and K = e B_{u u} /2mc the 'undulator parameter', e being the elementary charge, m the electron rest mass, c the speed of light, and B_u the peak field in the undulator. It is seen that very short photon wavelength can be achieved if only the electron energy (i.e. ) is chosen sufficiently high. However, in going to shorter and shorter wavelengths, several technical problems arise:

• For wavelengths below some 200 nm there are no good mirrors. This is the main reason why the shortest wavelength ever attained is 240 nm [3]. The solution is to operate the FEL in the amplifier mode, using an external input signal. To this end, however, a high power coherent input source (called seed laser) is necessary. Also, to achieve saturation within an undulator of reasonable length, very good electron beam quality is required. The gain length L_G (i.e. the photon power e-folding length) in the high-gain amplifier mode is given by [4]

with the FEL parameter (in this case for a helical undulator)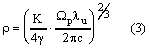

_p is the plasma frequency:

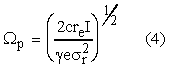
r_e being the classical electron radius, _r the rms electron beam radius and I the peak current inside the electron bunch. Besides these formulae there are others that also take into account 3D effects like electron beam emittance, photon diffraction[5] as well as quantum fluctuations[6], and there are various computer simulation codes. All of these indicate that, in the VUV, electron beam diameters of some 10^-4 m and peak current above 500 A are needed to achieve a gain length below 1 m and saturation within 20 m undulator length.

• Another complication arises if, in the wavelength regime envisaged, there is no seed laser. For this case is has been proposed to use the spontaneous radiation in the first part of the undulator as an 'input' signal [4,7]. This principle is called 'Self-Amplified Spontaneous Emission (SASE)'. It has been demonstrated successfully in the mm wave regime[8], and it is at present the subject of several proof of principle experiments at much shorter wavelengths (see below). The reason why SASE is specially attractive is that it does not rely on any atomic system's properties any more (thus allowing arbitrary tuning), and that it is the main candidate for getting into the subnanometer wavelength regime. For a diagram see Figure 1.

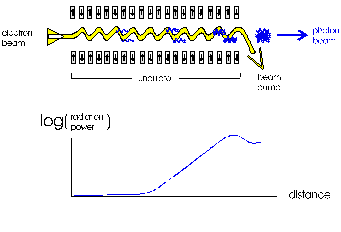
Amplified Spontaneous Emission = SASE" mode. The peak current in the electron bunch is very high and the undulator is long enough, so that power saturation is reached during a single passage starting from noise.

• For the high gain mode to work, a very demanding upper limit for the electron beam emittance has to be observed, see e.g. [9]:

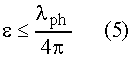
Fortunately it helps that the electron beam emittance decreases during acceleration - the Liouville Theorem for accelerated beams requires the normalized emittance to stay constant. Thus acceleration to the high , that is needed in order to satisfy the resonance condition (1) for short wavelengths, automatically decreases the emittance. Also, if diffraction effects are not very critical, condition (5) can be relaxed [5,6]. Nevertheless there remains a tighter and tighter tolerance on the normalized emittance of the electron source if one wants to attain shorter and shorter photon wavelengths.

The way to provide the required electron beam quality at the entrance of the undulator is determined both by physical limitations and technical possibilities. By extrapolating the present state-of-the-art beam parameters by a few factors of two, one can expect beam parameters as given in Table 1. At beam energy below some 200 MeV only more relaxed beam parameters can be realized due to space charge forces. With these values, a SASE FEL operating well below 100 nanometers could be realized. Schematically, such a machine is illustrated in Fig.2. Its essential components are:

• a low emittance photoinjector
• electron beam chicanes for longitudinal bunch compression
• accelerating structures with minimum wakefield effects
• a long undulator with very small field errors, preferentially with periodic focusing superimposed

Parameter	Units	Value
beam energy	MeV	> 200
rms energy spread /	10-3	1.0
n (normalized emittance)	mrad mm	2.0
rms bunch length s	mm	0.1
peak electron current	A	2000

Table 1: Typical electron beam parameters envisaged for VUV FELs.

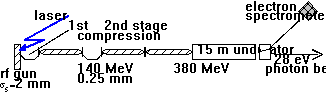
Electron source

The very small normalized emittance required by the transverse coherence condition (5) came within reach due to two major achievements: The development of the rf photo-injector gun [10] and the concept of space charge compensation[11].

In an rf gun, electrons are photo-emitted from a cathode which is placed in the split plane of an rf cavity and illuminated by a laser beam. Hence the electrons experience a high electric field from the very beginning (typically about 40 MV/m in an L­band gun ) and are rapidly accelerated, thus reducing space charge forces as quickly as possible. Since electrons start with nearly zero velocity, some phase slippage occurs with respect to the rf wave. The start phase ₀ is chosen so that the electrons travel near the crest of the wave at the exit of the cavity. The start phase is an important parameter to trade off transverse versus longitudinal emittance. With a fine adjustment of the phase either the minimum transverse emittance or the minimum longitudinal emittance can be optimized.

In spite of the very quick acceleration, there is still considerable emittance growth due to space charge forces. By applying solenoid focusing, a bunch rotation in phase space can be performed, such that there is mutual compensation of space charge effects before and after this focusing [11]. Geometry and focusing strength must be chosen such that this compensation is optimum just when further acceleration sets in (ultimately eliminating emittance growth as space charge effects scale with 1/²).

Longitudinal Bunch Compression

As mentioned before, a very high instantaneous beam current is needed in the undulator to reach photon power saturation within a reasonable undulator length. A typical number is 1250 A, corresponding to 100 m rms bunch length for a 1 nC bunch charge. This value is not attainable directly from the electron gun, because space charge forces would blow up both the transverse beam size and the momentum spread. Thus, the use of magnetic bunch compression is foreseen, in order to reduce the rms bunch length from an initial value of about 2 mm. In principle one could consider performing the bunch compression in one step at an energy level, where space charge is not critical any more (> 200 MeV or so). However, the cosine-like time dependence of the accelerating field would then impose an intolerable nonlinear correlated energy distribution along the bunch. The proposed solution is to perform compression in steps.

It is worth noting that multi-nC bunch compression below 100 m is an objective of the Accelerator Test Facility under construction at KEK, Japan [12] because it is an essential component of future linear colliders. It should also be noted that emittance conservation during bunch compression is a critical issue because of coherent radiation effects in the compressor[13,14].

Accelerator

The different linac concepts differ mainly with respect to the choice of rf frequency. Roughly speaking, larger rf frequencies (up to 30 GHz) offer a higher accelerating gradient, i.e. a shorter overall tunnel length, at the price of reduced power efficiency and worse beam energy distribution[27]. In contrast, low frequency linacs (down to 1.3 GHz for the superconducting TESLA linac) promise very good beam quality, because each electron bunch extracts only a small fraction of the large energy that is stored in the big cavity volume (small 'wakefield' effects)[31].

For a short wavelength FEL the highest priority is electron beam quality and large average beam current, while high accelerating gradient might be of secondary importance. Thus there is a clear preference for low frequency linacs. With respect to longitudinal wakefields of 200 fs long bunches, this preference is based on generally accepted scaling rules, because no experimental experience is yet available. Work is in progress to improve the understanding of these effects.

Undulator

The undulator is the most prominent FEL specific component. It has two functions:

1. It has to provide the sinusoidal field so that the FEL process can take place.
2. In order to keep the beam size small over the whole undulator length, an alternating field gradient caused by a superimposed quadrupole lattice has to be provided.

The main challenges are the total length of 10 m or more, the additional quadrupole focusing to be supplied and tight tolerances which need to be observed in order to guarantee permanent overlap of the electron beam and the photon beam.

Worldwide, several single pass FELs are either proposed or under construction to study lasing at shorter and shorter wavelengths. Table 2 gives an overview.

When	Where	Wavelength	Objectives
1996	UCLA	10 -20 m	start-up, growth rate [24]
1996	Los Alamos NL	16 m	start-up, growth rate [29]
1997	BNL	0.9 m	start-up, growth, saturation, tapering, short bunch, superradiance, harmon. generation [22]
1998	DESY TTF FEL Phase 1	50 - 100 nm	start-up, gain length, saturation [30]
1999	Spring-8 (if funded)	20 nm	start-up, gain length, saturation? [23]
2000	DESY TTF FEL Phase 2	6 nm	start-up, gain length, saturation, superradiance, harmonics....USERS [30]
2000	SLAC LCLS (if funded)	0.1 - 5 nm	dto., USERS [25,26]
>2000	Linear Colli-ders (if funded)	0.1 - 6 nm	dto., USERS [28]

Table 2: Overview of linac based FEL projects relevant to pave the way towards short wavelengths.

Various computer codes have been used to investigate the start-up from noise, and the lethargy, exponential and saturation regimes, respectively, e.g. NUTMEG [15], GINGER[16], FS2R[17], TDA[18,19], FELEX[20]. There is no essential disagreement between results of all these codes written by different groups and based on different approaches. A critical issue for a SASE FEL is to take into account the time dependence of the input noise and the slippage effects in the theory and in the simulations. A full 3D simulation of these processes has not been done yet.

A peculiar characteristic of the SASE FEL is the strong spiking both in the temporal and spectral domain of the emitted radiation[21]. It is a consequence of longitudinal subsections inside each electron bunch radiating at statistically independent phases if the start-up is from noise instead of being „seeded" by an external radiation field of high longitudinal coherence (i.e. by a „seed laser"). As a consequence, one expects large fluctuations of the instantaneous radiation power distribution inside each radiation pulse, changing from pulse to pulse, while the radiated power averaged over each pulse can be quite stable.

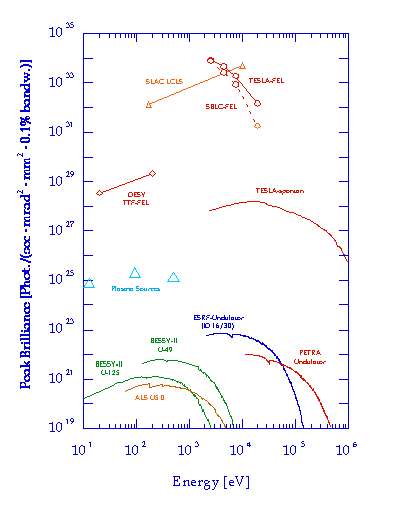
After saturation the SASE FEL behavior is determined by the nonlinear regime of the spikes. The total linewidth (half width half maximum) has been estimated using GINGER to be of the order of the FEL parameter as expected from the 1D time dependent model. As an illustration, Figure 3 shows predicted peak brilliance values for various radiation sources. It is seen that they exceed values of state-of-the-art radiation sources by several orders of magnitude. The average brilliance is also increased (however by a smaller factor), especially if a super-conducting, high average current linac is used, see Table 3.

As an alternative to the SASE concept, schemes generating harmonic content of the longitudinal electron density modulation at higher (up to say the 40th) harmonics of a conventional laser have been considered (multiple stage harmonic generation). An FEL using this principle is under construction at BNL [22]. Because start-up is not from noise, improved stability and longitudinal coherence are expected, at the price of more hardware complexity and limited tunability. Experimental experience on both SASE and harmonic generation is needed to find out which scheme is the most promising one towards ultra-short wavelengths.

Parameter	Units	Value
beam energy	GeV	1.000
ph (radiation wavelength)	nm	6.4 (193 eV)
u(undulator period)	mm	27.3
effective undulator length	m	25
rms beam size	mm	0.05
n (normalized emittance) in the undulator	mrad mm	2.0
peak electron current	A	2490
number of electrons per bunch		6.24E+9
number of photons per bunch		4E+13
rms energy spread /	10-3	1.00
rms bunch length s	m	50.
Lg (power gain length)	m	1.00
Psat (saturated power)	GW	3
average brilliance [photons/s/mm2/mr/0.1%]		up to 6E+21
bunch train length	sec	800
number of bunches per train		up to 7200
repetition rate	Hz	10

Table 3: Main parameters of the TESLA Test Facility FEL (TTF FEL)[30]. The insertion device is assumed to be a planar hybrid undulator. These values should be used as a guideline only since experimental experience has still to be gained in this wavelength regime.

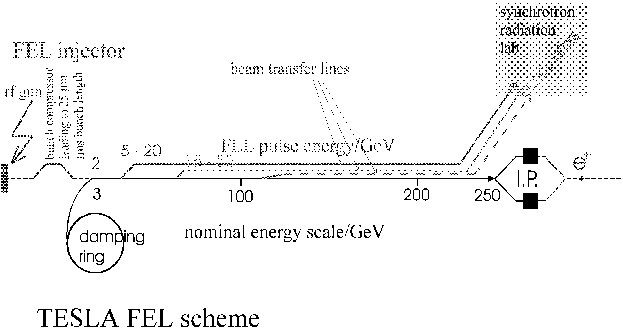
It is a most attractive feature of the SASE principle that there is apparently no wavelength limit, so that the idea came up to construct a SASE FEL operating in the Angstrom regime, i.e. on the natural scale of atomic physics and chemistry. This requires a very high quality electron beam in the energy range of 10 - 30 GeV. Since quantum fluctuation effects, which govern the electron beam size in a storage ring, are absent in a linac to a great extent, such high quality beams can only be provided by a linear accelerator. A first proposal of this kind came up at SLAC[25,26]. More recently it has been proposed to combine the construction of a future linear collider with installation of a multi-user X-ray FEL facility[28]. A linear collider is a pair of linear accelerators (each some 15 km long) directed against each other to collide electron and positron beams at 500 GeV center of mass energy, see e.g. [27].

The key point is that a linear collider also needs accelerator components capable of maintaining excellent beam quality during acceleration, but it cannot run, mainly for power consumption reasons, at high duty cycle. Therefore, the electron pulse structure consists of trains of electron bunches, repeated at the linac repetition rate f_rep , which is of the order of 10 Hz. It is proposed to run in an interleaved pulse mode, where rf pulses for high energy physics and those for X-ray physics alternate. For an X-ray FEL, only some 20% of the total collider length needs to be powered during the FEL pulses, so power consumption is not that much a concern - especially if a superconducting accelerator is used. Thus, the X­ray facility could utilize part of the expensive accelerator and the infrastructure of the high energy physics (HEP) lab without mutual interference, see Figure 4.

Note that such an operation mode consisting of alternating beam pulses for HEP and X-rays is different from so-called 'parasitic' use of HEP storage rings for synchrotron radiation users: Both users can define beam properties like energy, emittance, current, time structure etc. of their electron pulses independent of each other to a large extent, since they use different injectors and since it is no problem for rf components to change power and pulse length from pulse to pulse.

Fig. 4. Sketch of a Coherent X-ray source based on the TESLA linear collider installation. The beam can be extracted at any energy between 2 and 250 GeV and is transferred to the X-ray lab located close to the interaction points (I.P.). Many extraction lines could be considered in parallel, so that various beam energies are available in the X-ray lab quasi-simultaneously. The X-ray FEL electron beam is provided by an rf gun followed by a sequence of bunch compressors, while the high energy pulse is served by a damping ring.

[1] J.M. Madey 1971 J. Appl. Phys. 42 1906

[2] W. B. Colson 1996 Nucl. Instr. and Meth. in Phys. Res. A 375 669-671

[3] I.B. Drobyasko et al. 1989 Nucl. Instr. and Meth. in Phys. Res. A 282 424

[4] R. Bonifacio, C. Pellegrini, L.M. Narducci 1984 Opt. Commun. 50 373

[5] E.L.Saldin, E.A. Schneidmiller, M.V. Yurkov 1995 Physics Reports 260(4&5) 187-327

[6] J. Rossbach, E.L. Saldin, E.A. Schneidmiller, M.V. Yurkov 1996 Nucl. Instr. and Meth. in Phys. Res. A 374 401-407

[7] A.M. Kondratenko, E.L. Saldin 1980 Part. Accelerators 10 207

[8] T.J. Orzechowski et al. 1985 Phys. Rev. Lett. 54 889

[9] W.B. Colson, C. Pellgrini, A. Renieri (eds.) 1990 Laser Handbook 6, North Holland

[10] J. Fraser, R. Sheffield 1986 Nucl. Instr. and Meth. in Phys. Res. A 250 71, see also: J. Clendenin, this conference

[11] B. Carlsten 1989 Nucl. Instr. Meth. in Phys. Res. A 285 313

[12] F. Hinode, et al. (eds.) 1995 ATF Accelerator Test Facility Design and Study Report, KEK - Report

[13] Ya.S. Derbenev, et al. 1995 DESY Print TESLA-FEL 95-05

[14] Ya. S. Derbenev, E.L. Saldin, V.D. Shiltsev 1996 Proc. EPAC Barcelona

[15] E. T. Scharlemann, W.M. Fawley 1986 Proc. SPIE 642 1

[16]R.A. Jong et al. 1989 Proc. SPIE 1045 18

[17] E.L. Saldin et al. 1994 DESY Report 94-219

[18] C.-M. Tran, J. S. Wurtele 1989 Comput. Phys. Commun. 54 263

[19] P. Jha, J. S. Wurtele 1993 Nucl. Instr. and Meth. in Phys. Res. A 331 447

[20] J.C. Goldstein et al. 1989 Proc. SPIE 1045 28

[21] R. Bonifacio, et al. 1994 Phys. Rev. Lett. 73 70

[22] S. Krinsky (ed.), Jan. 1994 The BNL DUV FEL Report

[23] K. Yanagida, et al. 1996 Proc. FEL Conf. Rome, to be published in Nucl. Instr. Meth.

[24] G. Travish, et al. 1995 Nucl. Instr. and Meth. in Phys. Res. A 358 ABS 75

[25] C. Pellegrini et al. 1993 Nucl. Instr. and Meth. in Phys. Res. A 331 223

[26] R. Tatchyn, et al. 1996 Nucl. Instr. and Meth. in Phys. Res. A 375 274-283

[27] G. Loew (ed.): International Linear Collider Technical Review Committee Report 1995, SLAC-R-95-471 (1995)

[28] J. Rossbach, et al. 1996 Proc. FEL Conf. Rome, to be published in Nucl. Instr. Meth.

[29] R. Sheffield 1996 Proc. FEL Conf. Rome, to be published in Nucl. Instr. Meth.

[30] A VUV FEL at the TESLA Test Facility at DESY, DESY Print TESLA-FEL 95-03

[31] R. Brinkmann: Low frequency linear colliders, Proc. EPAC94, London , World Scientific (1994)