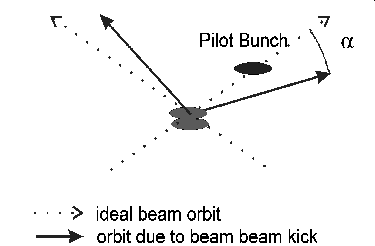
Fast ground motion will cause independent orbit movements in the two linacs of a linear collider such, that the beams may miss each other at the interaction point (IP). But even at rather large vertical beam-beam separations at the IP, beams will deflect each other through their electromagnetic fields. By measuring the position of a beam, which has just passed the IP and compare in it the position of a first pilot bunch -which does not have a partner in the opposing beam- with that of the following bunches in the same bunch train, the opposing beam can be steered with ultra fast kicker magnets for optimum collision at the IP. A feed-back system based on this principle will make the necessary steering corrections within a time short compared to the duration of the bunch train.

Fast beam steering at the interaction point, which relies on the beam-beam effect of colliding bunches, is a powerful tool to relax nanometer tolerances for final focus quadrupoles in linear colliders. Even betatron amplitude growth excited by vibrating quadrupoles further upstream in the linac, which is not filamented by the time the beam reaches the IP, can be corrected with fast beam steering. From Tracking calculations we expect only 30% filamentation over the entire length of the linac 1.

One stringent requirement for a feedback, which corrects the bunch train offset in the IP is, that the beam pulse is long compared to the overall processing time of the detected signal from the beam position measurement (BPM) to the kicker magnet. Parameters that influence this delay are the distance of the beam position monitor to the IP, the processing time of the feedback loop and the required magnetic field strength compared to the available peak power of the amplifier (compare Figure 1). The amplitude of pulse to pulse ground motion which can be expected from measurements done in the HERA tunnel, which is a tunnel under the city of Hamburg with an colliding beam facility, [2, 3] is approximately 70 nm rms for Frequencies below 1 Hz which is roughly six times the design vertical beam size. In order to limit the Luminosity reduction to 5%, the jitter at the IP should be smaller than 30% of the beam size, which is 5 nm in our case. A list of the interaction region parameters is extracted [4] from the complete list and given in Table 1.

One possibility to achieve this tolerance is to design a passive support system that keeps the final doublets at a given position over a time scale much larger than the repetition rate of the accelerator. This is certainly a challenging task for the technical design of the quadrupole supports which are part of the experiment of a linear collider. Vibrations from the linac quadrupoles are not correctable by this method with resonable effort.

Figure 1 Sketch of the interaction region layout and the location of the beam position monitor and the kicker magnet. The pilot bunch is the first bunch in the left train with no interacting counter part.

For the S-Band Linear Collider study two feedback loops are foreseen to relax this tolerance well beyond the measured value of 100 nm which was mentioned before. One loop relies on a direct measurement of the quadrupole vibration in combination with a mechanical (or correction magnet) feedback. Such a loop has been tested already and a suppression of a factor of 4 in amplitude for the rms value at 2 Hz has been proven 5. This feedback loops have mainly been developed to correct the linac quadrupole vibration. The second loop will be described in more detail in the following text.

The Principle of the Measurement and the Resolution

For a round beam the beam-beam force of two colliding bunches is proportional to the separation of the two bunches over approximately one . Operating with an aspect ratio(=_x/_y) of 20 (or more), as it is foreseen in Linear Colliders to reduce the beamstrahlung, produces an almost linear beam-beam force over approximately 10 _y. According to the beam-beam simulations using the parameters from Table 1, the kick angle per _y separation of the two colliding beams is given to within a good approximation by:

(1)

Let us assume that the BPM next to the IP is located at the position of the first quadrupole of the final doublet, which is 2 meters away. At this position the beam offset in the monitor according to formulae (1) would be 120 m per _y separation at the IP, which is easy to measure as compared to the 4 micrometer resolution being required for the rest of the linac BPM's.

A method based on beam-beam deflections to measure precisely the offset of the two colliding beams has been used for single bunch operation in the SLC from pulse to pulse already 6. On the other hand, a bunch to bunch measurement of the beam position, as being proposed for the TESLA Linear Collider study for both outgoing beams within one pulse can not be used, because of the delay time for signal processing as compared to the overall pulse length and bunch to bunch distance (compare Table 1). Therefore, in case of the S-Band Linear Collider study, a combination of both methods is proposed which uses a pilot bunch in one of the two colliding beam pulses and only a single BPM in combination with a single kicker magnet. Using such a scheme has the significant advantage, that almost no mechanical disturbance with an amplitude larger than a nanometer (vibration, girder resonance etc) can separate the colliding beams on the time scale of one bunch train length (2 sec -> 500 kHz), once they are colliding.

The Interaction Region Layout

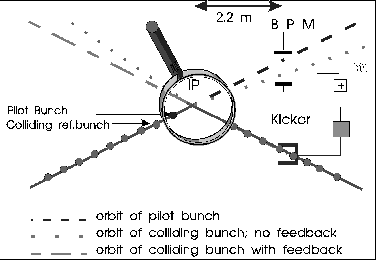
The location of the beam position monitor and the kicker has to be as close as possible to the IP in order to reduce the processing time of the feedback loop. Because the quadrupole next to the IP will have an integrated BPM the shortest distance is 2.2 meters from the IP. If the delays on cables, the response time of the feedback amplifier and the finite rise time of the kicker are added up, an overall delay of 50 nsec is expected. If we assume in addition that one bunch train will have a pilot bunch, the delay will increase to about 60 nsec. Therefore 3% of the 2 sec long beam pulse will not be corrected and, if far enough separated between pulses, will not contribute to Luminosity. In case of SLED operation with a 500 nsec long beam pulse, as foreseen for the energy upgrade to 800 GeV, the potential loss will increase to 12%. A continu-ous measurement of the beam­beam separation during the pulse will be done to correct even displacements which change along the bunch train.

The Kicker Magnet and Amplifier

The beam-beam force with flat beam operation is approximately linear over 10 _y.

In order to allow orbit corrections at the IP for a value of 150 nm, the required kick is only 0.07 rad, if a distance from the kicker to the IP as close as the BPM position is assumed. For the 250 GeV beam a magnetic field of 6
10^-5 T is sufficient. The kicker will be a stripline type kicker fed by two broad band amplifiers which can excite a maximum magnetic field of 1.1 10^–4. The parameters are given in Table 2.

The power amplifiers deliver a peak power of 2.5 kW each and have a bandwidth of more than 50 MHz to power each strip. A sketch of the kicker is shown in Figure 2.

In order to measure the beam position of the pilot bunch with respect to the colliding bunches an analogue delay will be used to subtract the two signals from the pilot bunch and the first colliding bunch directly. In addition the bunch intensity must be determined as well because the beam-beam kick is proportional to the bunch charge in the opposite beam. The resolution of the beam position measurement is 5 m 7 which is 4% of effect of a one _y separation and the bunch intensity measurement should be of the some order of magnitude. A sketch of the BPM set-up and the readout electronics design is shown in Figure 3.

Figure 2: Sketch of the Kicker magnet and the pulse forming network. (gibt noch ein besseres).

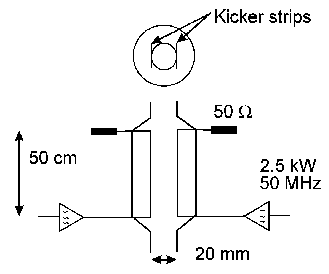
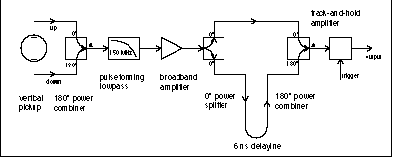
Figure 3: Schematics for the beam position monitor and the readout electronics.

Acknowledgment

The authors would like to thank S. P‰tzold, J. R¸mmler, and M. Wendt from DESY for their support and their contributions to the discussion on the possibilities to realize the required hardware for the feedback which is proposed in this paper.

1. Michael Drevlak (Darmstadt, Tech. Hochsch.), "On The Preservation Of Single Bunch And Multibunch Emittance In Linear Accelerators", DESY-95-225, Nov 1995. 148 pp. Doctoral Thesis.
2. V. Shiltsev, B. Baklakov, P. Lebedev (Novosibirsk, IYF), C. Montag, J. Rossbach (DESY), "Measurements Of Ground Vibrations And Orbit Motion At HERA", DESY-HERA-95-06, Jun 1995, 64 pp.
3. R. Brinkmann, J. Rossbach (DESY), "Observation Of Closed Orbit Drift At Hera Covering Eight Decades Of Frequency", DESY-HERA-94-04, Apr 1994. 10 pp, published in Nucl. Instrum. Meth. A350:8-12, 1994.
4. R. Brinkmann, R. Wanzenberg, "Improved Beam Stability with the New Parameter Set for the S-Band Linear Collider", this conference.
5. C. Montag, "Active Stabilization Of Mechanical Quadrupole Vibrations For Linear Colliders", DESY-96-053, Apr 1996. 24 pp., submitted to Nucl. Instrum. Meth. A.
6. P. Bambade, R. Erickson, "Beam-Beam Deflections as an Interaction Point Diagnostics for the SLC", SLAC-PUB-3979, May 1986.
7. W. Radloff, M. Wendt (DESY), "Beam Monitors For The S Band Test Facility", DESY-M-95-08AG, Jun 1995. 3 pp. Presented at 16th IEEE Particle Accelerator Conference (PAC 95) and International Conference on High Energy Accelerators (IUPAP), Dallas, Texas, 1-5 May 1995.