D. Raparia, J. G. Alessi, A. Kponou
Brookhaven National Laboratory
Upton, NY, 11973, USA
Quite good agreement has been achieved between computer modeling and actual performance of the Brookhaven 200 MeV Linac. We will present comparisons between calculated and measured performance for beam transport through the RFQ, the 6 m transport from RFQ to the linac, and matching and transport through the linac.
The Brookhaven 200 MeV linac serves as the injector for the AGS Booster and as well delivers beam to the Brookhaven Isotope Resource Center. It consists of a 35 keV magnetron surface plasma source, a low energy beam transport (LEBT) [1], 201 MHz radio frequency quadrupole (RFQ) [2], medium energy beam transport (MEBT) and 200 MeV Linac [3]. In this last year we have gone through a linac upgrade to get 2.5 more average current (146 µA) [4]. This was achieved by increasing repetition rate 5 to 7.5 Hz and increasing peak current from 25 to 39 mA. In this paper we compare computer modeling with actual performance.
LEBT had two pulsed solenoids, two sets of x and y steerer, beam chopper, emittance probe, and two current toroids. The chopper was removed from the line, making the line shorter by 70 cm. Computer modeling of this line showed that we should move the 1st solenoid as close to the ion source as possible to reduce the beam size in the 1st solenoid and the second solenoid as close to the RFQ as possible to increase the convergence angle required by the RFQ acceptance. Figure 1 shows the ion trajectories through this line and phase space at the exit of the ion source, middle of the line and entrance of RFQ. The RFQ acceptance is shown as a solid line ellipse. This calculation assumed that the beam space charge is neutralized.
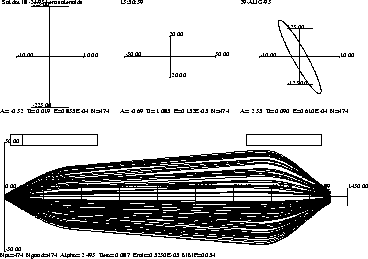
Figure 1: Ion trajectories through the LEBT and phase space
at ion-source, middle of the line, and at the entrance of the RFQ.
Shortening of the line resulted in lower measured emittance. Due to lower emittance and better matching transmission through the RFQ was improved by about 10 percent. Figure 2 shows the transmission as a function of input beam current.
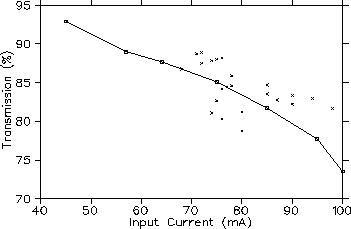
This is where we have recovered most of the beam losses.
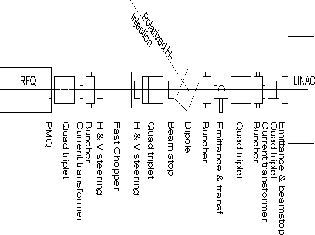
This line is 6 meter long and is shown in Figure 3. It consists of
four triplets, three bunchers, one slow chopper, one fast
chopper, two emittance measurement units, three current
transformers, two sets of x, y steerers, and a dipole to accomodate
polarized beam coming at 60 deg angle. The ideal match between RFQ and
DTL could have been obtained with a 5 
long FODO
lattice with quadrupole spacing about
and at least two bunchers. But the requirement of beam chopping and
polarized beam dictated a triplet solution [5].
The first quadrupole after the RFQ was too far; by the time the beam reached the quadrupole it had gone through a waist in the x plane, hence was diverging in both planes. No matter which polarity quad one puts, beam size in the other direction is very big. Also the longitudinal beam size is too big before it reaches the first buncher. To improve the capture and transmission of the beam in MEBT, the RFQ end flange at the high energy end was modified to accommodate a permanent magnet quadrupole (PMQ). The PMQ was similar to one as used in the SSC DTL [6]. We have also rearranged the gate valve and current transformers at the beginning of the line, and also measured and aligned all the quadrupoles very carefully. Measurement as well as simulation showed that as little as a 1.5 degree quadrupole rotation can increase the emittance by 50 %. The last quadruplet was changed to a triplet to reduce coupling. Figure 4, shows the measured and calculated phase spaces after the second buncher. Table 1 shows calculated (TRACE3D) and measured Twiss parameters for Figure 4.
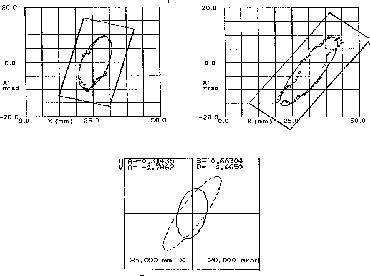
Table 1: Calculated and measured Twiss parameters after
the second buncher.
is in mm/mrad and (unnor.,RMS) in 
mm mrad.
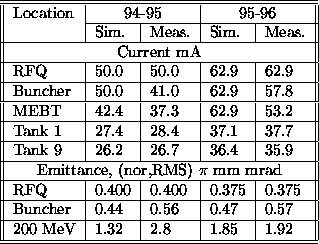
Table 2: Comparison between simulations and measured
beam parameters.
A radiograph of the beam at the BLIP target taken last year showed a
tilted ellipse in the x-y plane.
Sources of this coupling can be quad rotation
or vertical offset in the dipole. This triggered the need for an x-y density
profile. We found that algebraic reconstruction
technique (ART) could help us. ART was introduced by Gordan, Bender and Herman
[7] for solving the problem of three dimensional reconstruction
from projections. The ART algorithms have a simple intuitive basis.
Each projected density is thrown back across the reconstruction space in which
the densities are iteratively modified to bring each reconstructed projection
into agreement with the measured projection.
The reconstruction space is an n x n array of small pixels, 
is grayness
or density number which is uniform within the pixel but different from
other pixels.
Assume P is a matrix of m x n2 and the m component column vector
R. Let pi,j denote the (i,j)th element of P , and Ri denote
the ith element of reconstructed projection vector R.
For 1
im, Ni is number of pixels under projection Ri,
defined as 
.
The density number 
denotes the value of 
after q
iterations.
After q iterations the intensity of the ith reconstructed projection ray is
and the density in each pixel is
where Ri is the measured projection and,
and,
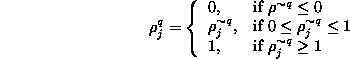
It is necessary to determine when an iterative algorithm has converged to a solution which is optimal according to some criterion. We are using as the criteria of convergence the discrepancy between the measured and calculated projection elements
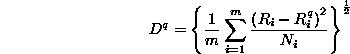
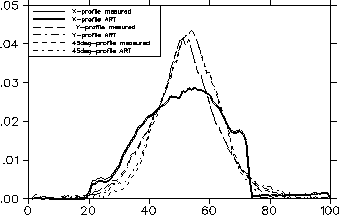
We have added a third wire at 45 degree in wire scanners in two places. Figure 5 compares the measured and reconstructed profiles in the BLIP transfer line [8] after the 1st octupole and figure 6 shows the reconstructed 3D density distribution.
Work performed under the auspices of the U. S. Department of Energy.
