Control of beam emittance is a key issue in the design of future linear colliders. Results depend closely on the assumptions made for the alignment tolerances of the various linac components. Processes involving several correctors and beam position monitors help either to reduce the emittance blow-up or to increase the tolerances beyond the values provided by simpler 'one-to-one' schemes. 'Dispersion-Free' or 'Wake-Free' algorithms require a simulation of the effects to be corrected, by lattice quadrupole detuning. Wakefield effects can also be measured, for example by current modulation as in the 'Measured-Wakefield' and 'Dispersive-Wakefield' processes.

For the Compact LInear Collider (CLIC) these algorithms, so far tested in the thin-lens approximation and assuming continuous scaling with energy of quadrupole strength and RF section length, are now applied on a more realistic structure of the main linac. Their implementation is described and the performances achieved in terms of the alignment tolerances are presented. Special emphasis is placed on the merits of the most powerful 'Dispersive Wakefield' process.

The virtues of trajectory correction processes involving several correctors and beam position monitors to control the transverse beam emittance in future linear colliders or to increase the alignment tolerances of the accelerator components have already been demonstrated. These processes are based on the minimization of an algorithm. This algorithm contains a term related to the nominal trajectory - measured with nominal beam and lattice parameters, in particular at the nominal momentum p₀ and bunch population N_p - and other terms dealing with trajectories taken under perturbed conditions, in order to evaluate the undesirable effects which need to be corrected. When only the term related to the basic trajectory is considered, the correction is named 'few-to-few'. Methods involving other terms have been presented several times; therefore, only their fundamental principles are recalled.

The undesirable effects can be simulated as in a 'Dispersion-Free' (DF) or 'Wake-Free' (WF) algorithm [1]. In a DF correction, the beam trajectory is measured for given beam-energy excursions p (typically p = 0.035 p₀ is adopted when applying the method on the CLIC linac model) and the differences between these and the nominal trajectory are corrected. A WF algorithm tries to evaluate the effects of the self-transverse wakefields within a bunch by the application of antisymmetrical perturbations on the lattice quadrupoles: when QFs are detuned by +, - is applied on QDs and vice versa. Again the differences with respect to the beam trajectory measured under normal conditions are minimized.

Instead of simulating these effects by quadrupole detuning, another possibility is to measure them. One needs to reproduce conditions which are free of the effects to be corrected and compare them to the nominal situation. There are various ways to evaluate the effects of transverse wakefields. In CLIC it has been shown [2] that on a beam trajectory measured with a bunch charge at least ten times smaller than the nominal one, transverse wakefield effects can be neglected. One can evaluate and correct the trajectory differences measured at these various currents. The method is called 'Measured Wakefields' (MW) correction [2]. In CLIC the method efficiency is improved by also incorporating a dispersive term in the algorithm (differences at low current between a bunch trajectory at nominal momentum and trajectories taken with energy excursions p). The measured wakefield effects and the dispersion effects can be further combined in a single term in the algorithm. This correction is named 'Dispersive Wakefields' (DW) [2].

These methods were applied on a model of the main linac based on the following assumptions: the thin-lens model for quadrupoles and continuous scaling with energy of quadrupole strength and of RF section length to ensure stability. With alignment tolerances increased to 10 m rms on pickups and cavities, DF and WF algorithms allow the normalized vertical emittance _y to reach values around 25 ¥ 10^-8 rad.m at 250 GeV for an initial emittance of 5 ¥ 10^-8 rad.m [3]. MW and DW corrections reduce this figure to _y = 10 ¥
10^-8 rad.m. A more realistic model of the main linac was developed [4] with finite cavity and quadrupole lengths, and divided into 6 sectors (for the 0.5 TeV CM energy option) with constant quadrupole length and strength within each. The various corrections have been adapted to this model; implementation and results are reported.

Initially, the implementation of the different corrections required three different programs.

Program 1 processes the transfer coefficients needed in the algorithm [2, 3], applying a kick unity and looking at the response on the subsequent pickups. Kicks are located at quadrupoles and the number of position monitors is a parameter; usually one monitor is placed on every other RF girder (2.8 metres). The whole linac model comprises 530 quadrupoles (kicks) and 1700 position monitors. For each kick, the response at 50 subsequent pickups is computed. This is performed for nominal conditions and for each perturbed situation required by the method; a minimum of three different machines is required for either correction.

Program 2 tracks the bunch, measures its trajectory under each appropriate condition (quadrupole strength, bunch charge) and can apply the kicks calculated by program 3. It generates alignment errors, applies corrections and stores trajectories. Both programs 1 and 2 derive from MTRACK [5, 6].

Program 3 actually applies the desired correction algorithm using the transfer coefficients from program 1 and the trajectories from program 2; different weights can also be applied to the various terms. Program 3 generates kicks which are then read by program 2 to measure the corrected trajectories. Programs 2 and 3 iterate along the whole linac.

The same architecture was kept for the new model with a few modifications because of the new linac structure. Some improvements were also implemented. Owing to the thick-lens treatment, it was necessary to consider quadrupole strength and cell length rather than phase advance and betatron wavelength. Matching between two consecutive sectors is required [4]; each matching section is precalculated (with MAD) for a given quadrupole gradient configuration. The three programs had to be adapted to the physical sectorization of the linac and overlapping between sectors was made possible. In program 1 the size of coefficient tables is reduced. For corrections, program 2 deals with quadrupole displacement during prealignment phases and with kicks, applied at quadrupole entrances during the application of more sophisticated processes. Program 3 was modified to deal with the new coefficient-table structure. During phases 1 and 2 only the relevant piece of linac is considered for a given kick or iteration. The procedure now works simultaneously in both the x and y planes; transverse coupling and quadrupole tilt are possible with a 4 ¥ 4 matrix formalism.

Once tested, the three programs were merged as subroutines of a single manager called CALICO (Correction Algorithms for LInear COlliders). The overall process efficiency is greatly improved in terms of simplicity and speed. The transmission of parameters between routines is easier, hence the procedure is simpler. A huge time saving has been achieved for transfer coefficient processing and correction application. CALICO is currently installed on the SP platform. The processing of the transfer coefficients for three different machine conditions requires 5 min and the application of an algorithm along the whole linac takes 10 to 15 min. Several corrections can now be tested in a short time.

DF and WF corrections

The application of DW or WF corrections requires, as observed for the thin-lens model, several passes, varying the linac section length considered during an iteration and the relative weight of each term in the algorithm until an acceptable solution is reached. With the new linac model, the application of DF or WF algorithms hardly results in a significant reduction of the emittance values obtained after prealignment. This was already stated in Ref. [7].

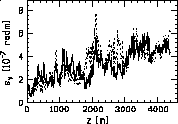
Figure 1 shows a typical result after a DF correction, requiring a total number of 90 iterations on linac sections of 12 quadrupoles; the trajectory term carries 10 times more weight than the dispersion. The final normalized vertical emittance is reduced from 6.0 ¥ 10^-7 rad.m (after prealignment) to 4.3 ¥ 10^-7 rad.m. The benefit of the DF correction is dependent on the position considered along the linac.

MW and DW corrections

As in the case of the thin-lens model, it was verified that a trajectory taken when the bunch charge is 12 times smaller than the nominal value is not affected by wakefields in the thick-lens model.

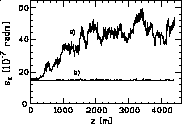
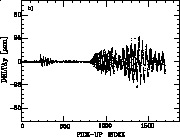
With rms alignment errors of 10 m on pickups and cavities, on a machine which is prealigned by the application of a 'one-to-few' correction, one pass (50 iterations) of the DW process leads to a reduction in the normalized emittance at the linac exit from 50 ¥ 10^-7 rad.m to 15 ¥ 10^-7 rad.m in the horizontal plane (see Fig. 2) and from 6 ¥ 10^-7 rad.m to 0.7 ¥
10^-7 rad.m in the vertical plane (Fig. 3), starting from 14.5 ¥ 10^-7 rad.m and 0.5 ¥ 10^-7 rad.m at injection. The dispersive term carries 100 times more weight than the trajectory.

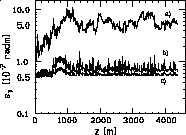
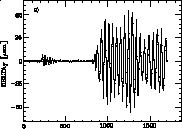
When alignment errors are reduced from 10 m to 5 m rms a final vertical emittance of 0.56 ¥ 10^-7 rad.m is obtained (less than 12% of blow-up) (see Fig. 3c). The better efficiency of a DW algorithm compared to a MW correction (which considers only the contribution of measured wakes without the dispersive term) is shown in Fig. 4. The efficiency of the DW method has been verified on five different machines (all having alignment errors of 10 m rms but different seeds). The average final vertical emittance value is 0.8 ¥ 10^-7 rad.m starting from 0.5 ¥ 10^-7 rad.m; the blow-up rate is 60%.

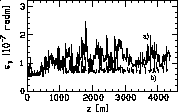
The DW method efficiency is also illustrated in Fig. 5, where the term describing wakefield effects (trajectory difference between a bunch with nominal charge and a bunch twelve times less populated) and the dispersive terms (trajectory difference between a bunch with nominal energy and a bunch with energy excursion) are represented. The correction is only applied on the first 800 pickups (2 km).

The same conclusions apply as in the case of the thin-lens model. The application of DF or WF algorithms requires difficult and time-consuming optimization of the various parameters (relative weights between terms, linac section length considered, microwave quadrupole setting) through several consecutive passes. It therefore relies strongly on the presence of diagnostics facilities. On the contrary, a single pass with the DW method allows direct convergence to final vertical-emittance values lower by a factor of 2-3 without requiring special optimization of these various parameters. Hence the power of the method can probably still be improved if one considers the various possible sophistications. The single-bunch vertical emittance blow-up rate in CLIC has now been pushed down to 50% for alignment tolerance values of 10 m rms which is a big achievement and could perhaps allow tolerances to be further increased.

We would like to thank T. D'Amico for his help in transferring the CALICO program from the VM to the SP platform. It is a pleasure to acknowledge the usual kindness and competence of the CERN Desktop Publishing Service.

[1] T. Raubenheimer, R. Ruth, 2nd EPAC, Nice, 1990.

[2] C. Fischer, 16th PAC, Dallas, 1995.

[3] C. Fischer, 4th EPAC, London, 1994.

[4] G. Parisi, G. Guignard, 4th EPAC, London, 1994.

[5] J. Tückmantel, CLIC Note 87, 1989.

[6] G. Guignard, 15th Int. Conf. H.E., Hamburg, 1992.

[7] C. Fischer, G. Parisi, CLIC Note 286, 1995.