Electromagnetic and particle-in-cell codes in two and three dimensions were used to design inductively detuned traveling wave cavities for the Relativistic Klystron Two Beam Accelerator (RKTBA) expected to extract high RF power at 11.424 GHz for an energy upgrade (TBNLC) to the Next Linear Collider, as well as for the prototype (RTA) being built at LBNL. Previous design was based mainly on 2D calculations. We will present full 3D simulations of a three-cell traveling wave structure in two configurations (with and without a choke structure), as well as preliminary cold-test results of a model cavity assembly.

A preliminary point design study for an rf power source based on the Relativistic Klystron Two Beam Accelerator (RKTBA) concept to extract high power at 11.424 GHz for the 1 TeV center of mass Next Linear Collider design has been presented recently by a LBNL-LLNL team [1]. The point design requires that the bunched drive beam delivers 360 MW of rf power with an rf current of 1.15 kA (600 A DC) in each of the 150 rf extraction cavities in a 300 m long RK-TBA. To achieve this goal, and to maintain longitudinal beam stability over long distances, the extraction cavity must be inductively detuned. To maintain low surface fields to avoid breakdowns, we consider traveling-wave output structures. The frequency-domain and time-domain computations were performed using the three-dimensional electromagnetic code MAFIA [2]. Based on the simulation results an experimental, cold test, extraction cavity was fabricated and tested. Initial S-parameter measurements show good agreement with numerical calculations.

The numerical effort for the physics design of the rf extraction cavity is based on calculations that are fully three-dimensional electromagnetic simulations of the complete cavity geometry including the output structures and the driving beam.

The favored type of simulations that we have been performing are the so-called "stiff-beam" calculations, where the beam excites the cavity to generate electromagnetic fields, but the fields do not act upon the beam. From this type of simulation we can calculate the electromagnetic fields and the wake potentials. The output power can be calculated as a function of time. The beam dynamics can be analyzed from the wakes potentials by beam dynamics code simulations [3,4,5].

The mesh size used is under one millimeter to accurately represent the cavity geometry. This type of mesh translates into a calculation involving about one million nodes. Furthermore, time steps of under 1 picosecond (dictated by the Courant condition for stable simulation) require running the calculation for several tens of thousands of time steps to simulate several tens of nanoseconds in order to have a smooth filling of the cavity and reach steady-state condition.

The beam is represented as a train of micro-pulses at the driving frequency. Each micro-pulse line-charge density shape is represented as the superposition of a constant term and three harmonics of the train frequency; this improves the numerical stabilty of the simulation.

The fully electromagnetic, three-dimensional code MAFIA has been the code of choice to perform all calculations. We have been using the frequency-domain as well as the time-domain modules. The alternate fully electromagnetic, three-dimensional Particle-In-Cell code ARGUS [6] has been used to cross-check the MAFIA calculations.

To avoid electrical breakdown, traveling-wave cavities are preferred over standing wave cavities since they generate lower surface electric fields for a given output power.

Present designs for the TBNLC extraction cavities evolve around traveling wave structures (TWS) with 3 cells of 8 mm inner radius; 180 MW of rf power is extracted through each of 2 separate ports in the third cell and transported via waveguides.

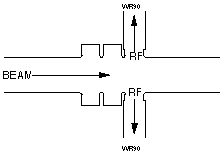
Fig. 1 shows a schematic of the 3-cell traveling wave output structure. A beam pipe length of 3.0 cm on each side is required to confine the electromagnetic field inside the cavity. The rf power is extracted through two WR90 waveguides attached to the last cell of the cavity.

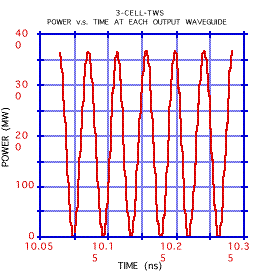
For this type of structure we have found a cavity design that delivers the right amount of power for the design parameters of the beam. Fig. 2 shows the calculated power as a function of time out of each WR90.

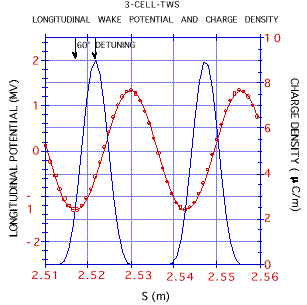
From the longitudinal wake potential we have found that the beam is detuned by 60° (lagging in phase). Calculations using the RKS code [3] have shown that this amount of detuning is required to obtain longitudinal beam stability for a long machine, as well as to sustain the level of output power for up to 150 structures. Fig. 3 shows the longitudinal wake and the beam profile for a detuned structure as a function of the distance from the beam-train head; in the micro-bunch frame, particles at the front lose energy and slow down, while particles at the tail gain energy, producing a bunching effect that counteracts the space charge debunching.

The peak surface electric field calculated is Å75 MV/m, a field that is within the upper limit in the peak electric field that has been imposed as a constraint in the design.

Transverse beam dynamics require low shunt impedances to avoid the beam break-up instability (BBU). Even when the 3-Cell TWS has low enough transverse impedance to avoid BBU [7], further damping of the high order modes is desirable to increase the confidence for the success of the accelerator as well as to relax tolerances on other parameters.

The addition of a cylindrically symmetric choke structure [8] to the 3-cell TWS, that confines the fundamental mode of the cavity while allowing high order modes to propagate out of the structure has been evaluated numerically.

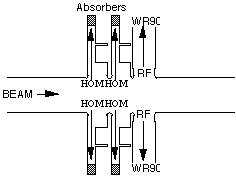
Figure 4. shows a schematic of the 3-Cell TWS with choke used in the simulation. The dimesions of the 3 cells are changed slightly to compensate for the effect of the choke structures in the resonant frequency; the output waveguides are the same as in the previous case.

It was found numerically that by a small change in the cavity dimensions, to keep the resonant frequency constant, the cavity could extract the same amount of power from the beam while maintaining the inductive detuning. Even when this design was not optimized the transverse impedance calculated decreased appreciable by the introduction of the choke.

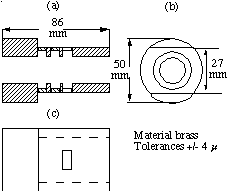
An experimental 3-cell traveling wave extraction cavity was designed and fabricated. The design is based on the results of the 3D computer simulations. Since cold tests do not present any break down or vacuum requirements the cavity mechanical design is rather simple, allowing a quick and flexible assembly of the cavity. The cavity assembly shown in Fig. 5 consists of from 1 to 5 cells and two 30 mm long end beam pipes. One of the cells contains the two extraction apertures connecting to the WR90 waveguides. The test cavity is made from brass to reduce manufacturing costs.

Cold test measurements can be used to validate the results of the electromagnetic computer calculations by measuring the frequency-dependent S-parameters of the extraction cavity. Furthermore the measurements may allow the optimization of the extraction cavity geometry by evaluating the loaded Q of the cavity.

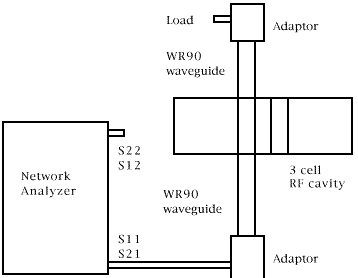
The test is performed in the LBNL Lambertson Beam Electrodynamics Laboratory using the HP 5810 RF vector network analyzer. Fig. 6 shows the test system layout. The network analyzer oscillator signal is introduced through a WR90 waveguide in one extraction aperture while the second aperture, through a WR90 waveguide, can be connected to a matched load, short, open or to the network analyzer's second channel.

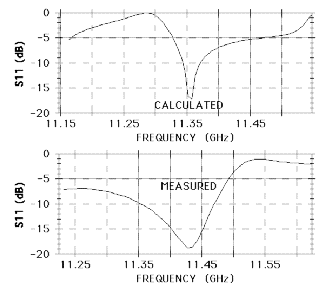
The cavity S-parameters are measured for cases when the second extraction aperture is terminated with a short, open, and a matched load. Fig. 7 shows an example of a frequency dependent S11 measurement in agreement with MAFIA calculations. The frequency shift, and the difference in the loaded Q, between the calculated and measured S11 behavior is probably due to the resolution of the calculation. The final tuning of the system can be done by readjusting the dimensions of the cavity using the above measuring procedure.

Future plans include the extension of the measurement system to frequency perturbation techniques using moveable dielectric rods or beads inside the cavity structure to evaluate the R/Q and the electric field variation along the cavity.

We are indebted to J. Corlett for helpful discussions and advice in the use of the LBNL Lambertson Beam Electrodynamics Laboratory.

[1] Yu, S.S., Deadrick, F., Goffeney, N., Henestroza, E., Houck, T., Li, H., Peters, C., Reginato, L. Sessler, A., Vanecek, D., and Westenskow, G., "Relativistic-Klystron Two-Beam Accelerator Based Power Source for a 1 TeV Center-of-Mass Next Linear Collider - Preliminary Design Report," Report UCRL-ID-119906, LBNL-LLNL, 1995.

[2] The Mafia Collaboration, "User's Guide, MAFIA Version 3.x". Darmstadt, Germany, 1992.

[3] Li, H, and Yu, S.S., "Theory of Inductively Detuned Traveling Wave Structures," Nuclear Instruments and Methods in Physics Research A361, p. 21, 1995.

[4] Houck, T.L., Westenskow, G.A., and Yu, S.S., "BBU Code Development for High-Power Microwave Generators," Proceedings of the 16th International LINAC Conference, Ottawa, Ontario, Canada, p. 495, 1992.

[5] Kim, J.S., Henke, H., Sessler, A.M., and Sharp, W.M., "The Standing Wave FEL/TBA: Realistic Cavity Geometry and Energy Extraction", Proceedings of the 1993 Particle Accelerator Conference, p. 2593, 1993.

[6] Chang, C.L., et al., "Three-Dimensional Modeling of Accelerators", LA-11857-C, 1990.

[7] Giordano, G., et al., "Beam Dynamics Issues in an Extended Relativistic Klystron," Proceedings of the 1995 Particle Accelerator Conference, p. 740, 1995.

[8] Shintake, T., "The Choke Mode Cavity," Jpn. J. Appl. Phys. Lett, 31, p. 1567, 1992.

* Supported by DOE SBIR grants DE-FG03-95ER81974 and DE-FG03-96ER82179, by DOE contract W-7405-ENG-48 (†), and by DOE contract AC03-76SF00098 (††).