There is an interest in using multiple-beam RFQ (MB-RFQ) with a high packing of beamlets for a variety of purposes. The principle of the MB-RFQ arranged as a matrix array of longitudinal rod-electrodes is known for a long time. It allows to reach a packing factor up to 40%. The unsolved problem is to define such configuration of resonator, which preserves a high packing without disturbing RFQ fields and correctly excites electrodes surrounding every channel.
According to the usual design principle, which is extended from a single-channel 4-rod RFQ to MB-RFQ resonators, every electrode of MB-RFQ must be discretely connected with tank by coupling elements, while adjacent RFQ electrodes having different potentials cannot be interconnected by short-circuited couplers and the couplers may interconnect only next adjacent electrodes "in a chess order", avoiding adjacent electrodes. The principle reduces a packing factor considerably from the above value.
A new principle for MB-RFQ is suggested. A high packing
factor is preserved, because of discrete connections of adjacent
electrodes are allowed. The beam dynamics in RFQ-channels is modified.
Beams perform "slalom" motions, utilizing intrinsic
transverse oscillations. Essential design issues are discussed.
In recent years, many ion sources with a broad-beams
have been developed [1-3]. The broad-beams are formed as multiple-beams
consisting of an array of identical single-beams (or beamlets).
The beamlets are packed very closely. The packing factor defined
as a ratio between the sum of areas occupied by beamlets and a
total area of broad-beam can reach 40-50 %. The number of beamlets
may achieve several hundreds (or even thousands). Transverse size
of broad-beam can be up to one meter or more.
There are applications, which require MeV-range broad-beams, e.g. heating of plasmas in magnetic confinement devices [3]. Existing broad-beam accelerators use the electrostatic method of acceleration. Because of technical problems due to the voltage breakdown, an attainable level of beam energy is restricted. Perhaps, some RF-acceleration method adapted to a multiple-beam acceleration may be applied for MeV-range broad-beam accelerators. Many RF multiple-beam accelerating structures had been already presented in the past years [4-13].
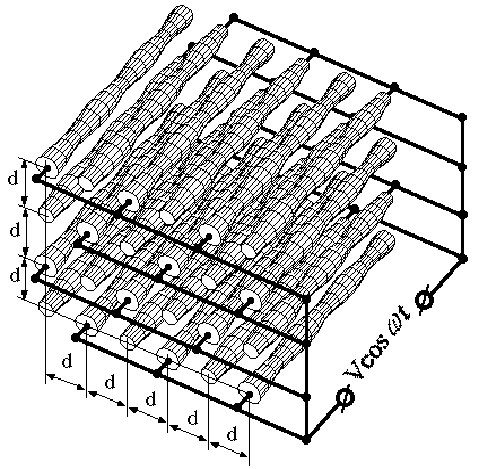
MB-RFQ arranged as an array of longitudinal rod-electrodes
(see Fig. 1) is known for a long time [4,7,9]. It is required
to realize a high packing factor without disturbing RFQ fields
and excite correctly electrodes surrounding every channel. In
this paper, we try to find out possible configurations of the
MB-RFQ structures satisfying the above requirements.
Resonators with coupling stems
Known MB-RFQ structures [4,7,8-12] are designed using a periodical multiplication of an single-channel 4-rod RFQ in the transverse direction. RFQ-electrodes in a matrix array should be discretely supported by some transverse stems or coupling elements. Adjacent electrodes have different potentials along the whole structure. They can not be interconnected by short-circuited couplers. Only next adjacent electrodes may be interconnected "in a chess order".
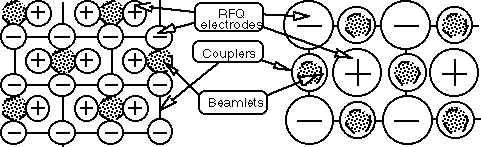
Two possible configurations of couplers consisting
of ideal thin conductors are shown in Fig. 2. In the first (left)
configuration, coupling conductors bypass the RFQ-channels. Only
a quarter of RFQ-channels is used. The second (right) configuration
allows the penetration of the coupling elements inside RFQ-channels.
The couplers have aperture-holes. The original RFQ-fields are
distorted in this configuration.
In order to prevent voltage breakdown, the realistic
configurations should be composed of thick conductors. The curvature
radii of all conductors could not be less than the curvature of
RFQ-electrodes. We tried to design such couplers. However, the
packing factor is reduced to 5% and 10% for the left and right
configurations, respectively.
A quarter-wave short resonators
To preserve the packing factor, MB-RFQ resonators can be designed without coupling elements. The RFQ-electrodes are only connected to the tank bottoms, and the length of MB-RFQ resonator, l is about a quarter of the wavelength l. The MB-RFQ accelerator is composed of several short resonators.
Two types of such resonators are known [7,8,10].
In the first type, all RFQ-electrodes are connected to the one
bottom of the tank and have open ends at the another bottom. In
the second type, all electrodes are divided into two groups in
a chess order. The electrodes of two groups are connected to the
tank in opposed manner. Figure 3 shows the example of the second
type of the resonator.
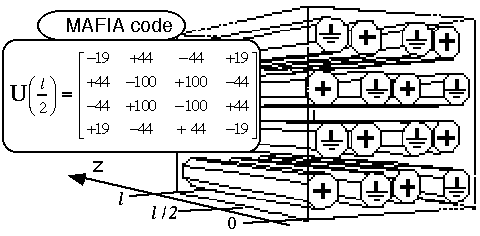
The resonators with 4x4 matrix arrays of RFQ-electrodes have been studied with MAFIA code [14]. The first type provides correct quadrupole excitation of electrodes when the tank cross-section is a square with the side 4d, where d is the distance between axes of adjacent electrodes. This resonator can be used as an RFQ matching section, because RFQ voltage increases along the resonator as a sine function.
The second type of the resonator does not provide
correct quadrupole excitation of the electrodes. The voltage amplitudes
at the middle of the resonator are shown in the Fig. 3. The voltages
on the electrodes surrounding RFQ-channels deviate from quadrupole
symmetry. It is difficult to adapt this type of resonator to MB-RFQ-acceleration.
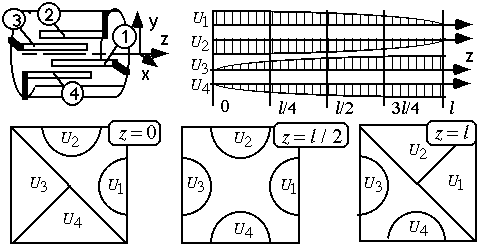
Let us find out a type of a resonator, which allows a short-circuited connections between adjacent electrodes. Figure 4 shows a unit module of such resonator.
To provide RFQ-acceleration, the field at the resonator axis should be the same as in a conventional RFQ-channel. It is described by the following lowest-order electric-field potential function [15,16]:
At every cross-section of the resonator, its conductors
have some definite voltages ![]() ,
, ![]() ,
,
![]() , and
, and ![]() . To provide
the RFQ fields described by Eqs. (1), surfaces of the RFQ pole
tips for every conductor is defined by equation:
. To provide
the RFQ fields described by Eqs. (1), surfaces of the RFQ pole
tips for every conductor is defined by equation:
Figure 4 shows pole tips at the ends and the middle
of the resonator. The RFQ-channel has a zero optical transparency,
and could not provide a conventional RFQ acceleration. The beam
dynamics must be modified in this case.
We have revealed a possible way to provide RFQ acceleration
in this accelerating channel. It is based on the fact that parts
of beam coherently oscillate around the axis during transverse
oscillations in a strong-focusing quadrupole channel. Figure 5
shows particle motion calculated by PARMTEQ code [16] in transverse
plane, X0Y. Part of beam injected in the first quadrant of the
X0Y-plane performs periodical excursions between the first and
the third quadrants of X0Y-plane. This part of the beam can be
transported in the accelerating channel of the new resonator,
if space period of transverse beam oscillations ![]() is equal to
is equal to ![]() ,
,
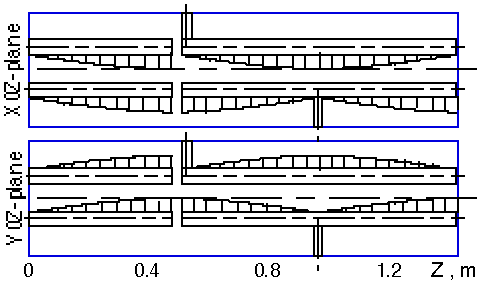
To test this principle, numerical simulations have been done. Figure 6 shows the resonator of the simulated accelerating structure. It consists of a quarter-wave matching resonator and two sections of the new resonator.
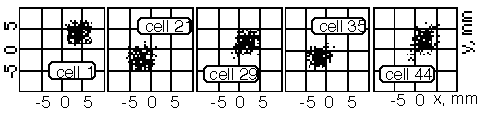
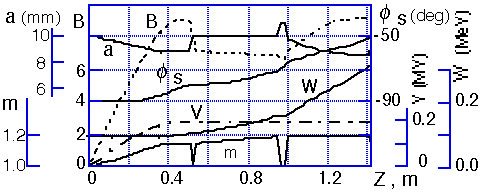
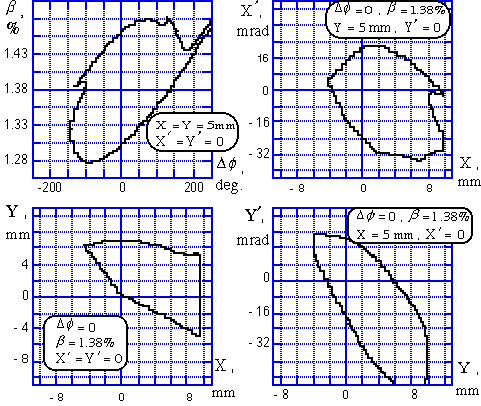
The design parameters of RFQ-channel calculated by PARMTEQ code are presented in Fig. 7. The pole tips of RFQ-electrodes have been obtained by a numerical solution of Eqs. (2). The beam dynamics had been calculated using beam dynamics code DYN1 written by V.Kapin. Figure 8 shows the example of the beam-structure and the electrode profiles in the X0Z-plane. Similar picture exists for X0Y-plane. Beam performs "slalom" motions, avoiding pole tips. Acceptances of the RFQ-channel are presented in Fig. 9. The results of the test calculations show principal possibility of beam acceleration in the new RFQ-channel.
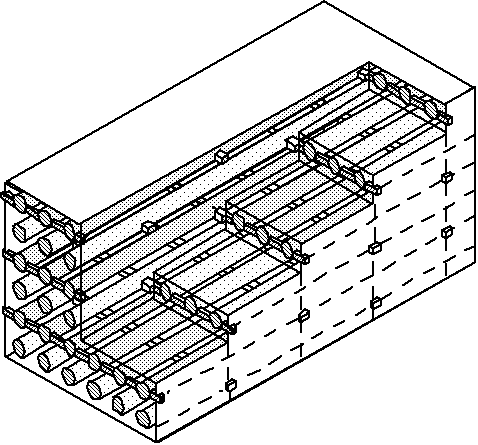
The MB-RFQ resonator designed by a multiplication
of the new 4-rod RFQ in the transverse direction is shown in the
Fig. 10. The MAFIA calculations have shown the existence of the
necessary mode of field oscillations in this structure.

[1] A.Forrester, Large ion beams: fundamentals of generation and propagation, 1988 by John Wiley & Sons, Inc.
[2] I.G.Brown, Rev.Sci.Instrum., 65(10), 1994, p.3061.
[3] Y.Okumura et al., Rev.Sci.Instrum., 67(2), 1996, p.1018.
[4] D.A.Swenson, Proc. of the Heavy Ion Fusion Workshop, Berkeley, 1979, LBL-10301, SLAC-PUB-2575, p. 239.
[5] Ion Linear Accelerators, ed. by B.P.Murin, Vol. 1, Atomizdat, Moscow, 1978 (in Russian).
[6] R.M.Mobley et al, IEEE Trans. on Nucl. Sci., Vol. NS-28, No.2, 1981, p. 1500.
[7] E.V.Gromov et al., Inventor's Certificate of USSR No.831044, Bulletin of inventions, 1985, No. 12 (in Russian)
[8] H.Klein et al., Proc. of the 1981 Linear Accelerator Conference, Santa Fe, LANL report LA-9234-C, p. 96.
[9] P.Junior et al., IEEE Trans. on Nuclear Science, Vol. NS-30,
No. 4, 1983, p. 2639.
[10] E.V.Gromov and S.S.Stepanov, Proc. of MEPhI's collected papers, Moscow, Energoatomizdat, 1983, p.35 (in Russian).
[11] R.J.Burke et al., IEEE Trans. on Nuclear Science, Vol. NS-32, No. 5, 1985, p.3347.
[12] R.J.Burke et al, Nucl. Instrum & Meth., Vol. B10/11 (1985) p.483.
[13] J.Madlung et al., Proc. 1995 Particle Accelerator Conf., Dallas, 1996 by IEEE, p.908.
[14] R.Klatt et al., Proc.1986 Linear Accelerator Conf., 1986 by SLAC, p. 276.
[15] I.M.Kapchinskiy, Theory of resonance linear accelerators, 1985 by OPA (Amsterdam).
[16] K.R.Crandall et al., Proc. of the 1979 Linear
Accelerator Conf., 1980 by Brookhaven Nat. Lab., BNL-51143, p.
205.