The Accelerator for the Production of Tritium (APT) requires a very high proton beam current (100 mA cw). The requirement for hands-on maintenance limits the beam spill to less than 0.2 nA/m along most of the linac. To achieve this goal, it is important to understand the effects of fabrication, installation and operational errors, establish realistic tolerances, and develop techniques for mitigating their consequences.
A new code, PARTREX, statistically evaluates the
effects of alignment, quadrupole field, and rf phase and amplitude
errors in the linac. In this paper we review the effects of quadrupole
misalignments and present two steering algorithms that minimize
the potential for particle loss from the beam halo. We tested
these algorithms on the 8-to-20-MeV portion of the APT linac.
To meet the beam loss criteria, the APT design [1] incorporates a very strong magnetic focusing lattice that maintains a small well defined beam in transverse space. The apertures of the accelerating structures are sized, with consideration to power, to give maximum clearance to the beam. We expect beam halo to be the main source of particle loss. The linac design avoids known causes of halo growth, such as lattice discontinuities, beam mismatch and large beams. Opportunities for beam excursions both longitudinally and transversely have been minimized.
Following the RFQ a coupled-cavity drift-tube linac
(CCDTL) accelerates the beam from 6.7 to 100 MeV and a coupled-cavity
linac (CCL) accelerates it to a final energy of 1.3 GeV. The resonant
rf structure is integrated with a FODO electromagnetic-quadrupole
(EMQ) focusing lattice having a constant period of 8 (=relativistic
particle velocity, =free-space rf wavelength at 700 MHz). The
EMQs are approximately centered in the spaces between cavities
as shown in Fig. 1.
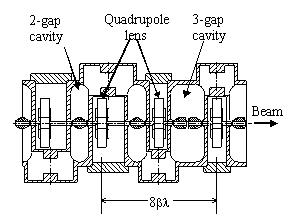
Beam spill can result from beam halo and transverse beam excursions. Mismatches between the beam and the focusing lattice cause the beam halo to grow. Misalignments of the EMQs cause beam excursions. Besides the EMQs, the beam-position monitors (BPMs) that detect the trajectories of errant beams have tight tolerances. The lenses are very strong to maintain a small beam size and as a consequence of their strength, the beam trajectory is very sensitive to their alignment. It is even more important to accurately align the BPMs to avoid unknowingly missteering the beam, which would compound the effect of the EMQ misalignments.
Two effects relax the alignment tolerance on the accelerating structure itself. The rf fields have a very small influence on the beam's transverse motion so cavity misalignments primarily reduce the clear aperture. Because the beam is largest in the EMQs, spill is more likely there than in the rf structure even with a reduced aperture.
We have evaluated three effects that influence the alignment. Beam steering and repositioning of EMQs correct for static misalignments. We do not actively correct for dynamic misalignments. We will minimize vibrational errors through careful design of the support stand and by decoupling all driving forces such as coolant manifolds. We will correct long term misalignments, arising from settling and ground movement, manually by using a laser based reference line and alignment scheme.
Quadrupole doublets in the LAMPF CCL vibrate with a measured amplitude of 0.0003 in. at harmonics of 30 Hz. [2] The driving force comes from a shaft imbalance in the pumps and motors. The accelerator support stand holding both the accelerator and manifolds has a natural mechanical frequency that is a subharmonic of the pump frequency. Based on this study, we have set the dynamic alignment tolerance at 0.0001 for the APT linac EMQs.
The EMQs are of conventional design and are mounted independently of the accelerating structure in the inter-cavity spaces as shown in Fig. 1. Their integrated field of 2.625 T for the 8 lattice period produces a zero-current transverse phase advance of about 80/period. The steering coils, shown in Fig. 2, on the magnet yolk produce a dipole field superimposed on the quadrupole field. Saturation in the pole tips and undesirable sextapole field components limit the useful steering. All EMQs will include steering windings for both axis. We will connect power supplies to these windings as required.
The beam centroid will be located in the linac using 4-lobe microstrip transmission-line detectors (BPMs) that measure the image currents of the beam traveling along the wall of the beam tube. Figure 3 shows a BPM that will be located inside a quadrupole between two cavity segments.
We will put the magnetic center of each EMQ and the electrical center of each BPM on a common line within a given tolerance. The bore of the EMQs will be inaccessible after installation. Therefor before installation we will align the magnetic center of each EMQ to its mounting fixture. Each lens will then be mounted kinematically, independent of the linac, on rails attached to the support stand which have been aligned to a smooth and continuous reference line extending the length of the accelerator. Table 1 lists four operations whose tolerances contribute to the final accuracy in locating the lenses.
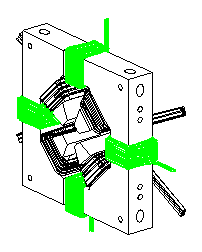
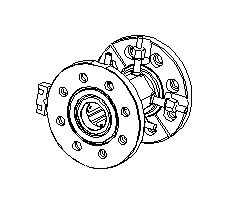
Table 1. Local EMQ Alignment Budget
| Magnetic center to mounting fixture | |
| Magnet mount to support rail | |
| Support rails to reference line | |
| Reproducibility of the reference line | |
| Cumulative tolerance (quadrature sum) |
Reliably reestablishing a reference line running the length of the accelerator may be the most challenging of these to achieve. Techniques to achieve this alignment are under investigation. The expected long term motion of the tunnel, renders fiducials useless so we plan to use a laser beam to establish the reference line.
Like the lenses, the electrical axis of each BPM must be referenced to its mounting flange before installation. Conventional techniques determine its installed position, relative to the reference line. The measured offsets are entered in the control system data base. Table 2 lists four operations whose tolerances contribute to the final accuracy in locating the BPMs.
Table 2. Local BPM Alignment Budget
| Electric center to mounting flange | |
| Location of flange relative to support rails | |
| Support rails to reference line | |
| Reproducibility of the reference line | |
| Cumulative tolerance (quadrature sum) |
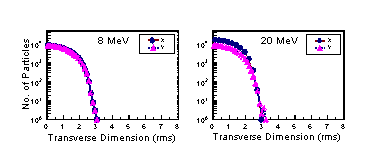
The beam emerging from the RFQ is small and very well defined. Careful matching and strong focusing preserve its quality for a very long distance in the APT linac. Figure 4 shows the transverse profile of a 100 mA beam from a PARMILA simulation using 100k particles and a 2-D (r-z) space charge routine. The total beam size in both planes remains within 3 through 20 MeV.
We have written a new version of PARMILA (PARMILX [3]) that generates three types of linac structures: DTLs, CCDTLs and CCLs and simulates their performance. For error studies, beam steering and matching algorithms, and linac commissioning methods, we have developed a companion code PARTREX (similar to PARTRACE [4]). PARTREX generates the same linac and follows the beam center in exactly the same way that PARMILX does but represents the beam by an ellipsoid. PARTREX can carry out multiple simulations rapidly, and the effects of various errors such as quadrupole misalignments are quantized by probability distributions.
To study the effect of quadrupole displacements, PARTREX applies random displacements, within a specified tolerance, to the position of each EMQ. It then records the maximum displacement of the beam center and the maximum beam radius. With multiple runs (100), each using a different set of random errors, we analyze the probability that the maximum beam displacement or beam radius might exceed acceptable limits. Studies with different tolerances can reveal the probability that a specified tolerance will result in beam spill, or alternatively, can indicate how often corrective action (i.e., steering) must be taken.
PARTREX represents the beam in transverse space by
an ellipse. The semi-axis are a function of the beam emittance
and the total beam size which is specified by the user in units
of rms () beam size. A value of 3 (typical) means that the edge
of the beam (for purposes of this study) is assumed to be at 3.
As the beam traverses a sequence of misaligned lenses, its centroid
is displaced from and oscillates about the linac axis. The beam
radius Rb, is defined to be the maximum distance from
the linac axis to the outer edge of the beam ellipse. The aperture
radius is Ra and we define a filling factor F= Rb/Ra.
At some point F will reach a maximum value, Fmax, which is recorded
for each run. Fmax=1 means that the edge of the beam is just scraping
the aperture.
Using PARTREX we investigated several steering schemes for the APT linac. We tested these algorithms in the 8-to-20-MeV section that includes 177 cells and 60 EMQs. The simplest scheme is to steer at one focusing EMQ to put the beam on-axis at the BPM located in the next focusing EMQ. We then steer in this second EMQ to put the beam on axis again at the BPM in third focusing EMQ. Because the phase advance between the steering magnets and BPMs is 80 nom., this procedure does a good job of restoring errant beams. However, BPMs can be costly, and we would like to minimize their number and still assure minimum beam spill.
We have investigated a number of variants on this scheme. We present a representative scenario in which this steering set, comprised of two dipoles and two BPMs in 5 EMQs, is repeated every 4.5-lattice periods. The diagram below shows this schematically. We steer in both planes of each steering EMQ.
EMQ +-+-+-+-+-+-+-+-+-+-+-+-+-+
Steering x&y s.s......s.s......s.s.....s
BPM ..b.b......b.b......b.b....
Figure 5 shows the result of 100 PARTREX runs in which we have assumed a 3 beam and an alignment tolerance of 0.005 in. for both EMQs and BPMs. The left-hand plot shows the probability distribution for the maximum horizontal excursion of the beam centroid (Xbar max) from the linac axis. The dashed curve represents a misaligned linac with no steering while the solid curve corresponds to the application of the steering algorithm described above. Without steering we expect a maximum excursion of 2 mm on the average (0.5 on the ordinate). In the worst case it would reach 4.5 mm. Steering reduces these values to 1 and 2 mm respectively.
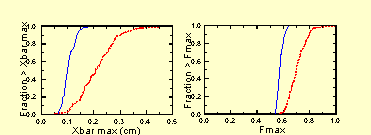
The right-hand plot shows the corresponding probability distributions of Fmax. Without steering, the beam will fill 70% of the bore on the average and just scrape in the worst case. A steered beam will fill 57% of the bore on the average or 65% in the worst case.
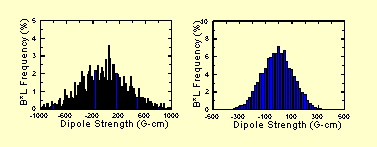
This steering scheme does a good job using few BPMs
but at the cost of unacceptably large dipole fields. The left-hand
plot in Fig. 7 shows the frequency distribution of the expected
dipole strengths. Integrated steering fields as high as 1000 G-cm,
which are required in some cases, exceed the practical limit of
our EMQ design.
A second steering scheme uses multiple steering magnets (10-20 nom.) followed by a pair of BPMs. Since there are many more variables (steering magnets) than constraints (2), there is an infinite number of solutions. However, there is a unique solution that also minimizes the steering required in each magnet, which is the one we want. We find a least-squares solution with constraints by minimizing the sum of the squares of the steering fields while constraining the beam center to the axis at the two BPMs. This scheme works extremely well, in that few position monitors are required and the magnitude of the steering fields are well within practical limits.
We have investigated a number of variants on this scheme. We present a representative scenario, shown schematically below, in which BPM pairs are located in quads of the same sign every 7.5-lattice periods. We steer in the focusing plane only of each EMQ.
EMQ +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-
X steer s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.
BPM ............b.b............b.b..
Y steer .s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s
Figure 6 shows the results of 100 PARTREX runs assuming the same conditions and conventions described in the previous section. In this case the steered beam (solid curves) experience slightly smaller excursions than in the previous example. Figure 7 shows that the expected dipole strengths, using the least-squares steering method, are all within 300 G-cm.
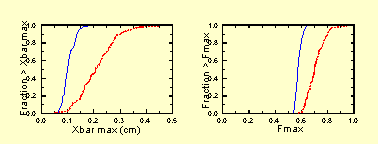
We have discussed two alignment algorithms
for the APT linac. Simulations show that for the expected alignment
tolerances both do a good job of preventing excursions leading
to beam spill. Least-squares steering, although requiring more
dipoles, keeps the fields in all magnets within an acceptable
range because the task is shared by many magnets.
[1] S. Nath et al., "Physics Design of APT Linac with Normal Conducting RF Cavities," this conference.
[2] Los Alamos National Laboratory Internal Memorandum ESA-MT/C931
[3] H. Takeda et al., "Modified PARMILA Code for New Accelerating Structure," Proceedings of the 1995 Particle Accelerator Conference and International Conference on High Energy Accelerators, Dallas, Texas, May 1-5, 1995.
[4] K. R.
Crandall, "Error Studies Using PARTRACE, a New Program that
Combines PARMILA and TRACE 3-D", 1988 linac conference, Williamsburg,
Va.
*Work supported by the US Department of Energy.
**AMPARO Corporation, Santa Fe, NM 87504