The numerical model of EBIS is presented. The calculation of Kr ionization by cooling with Ne ions was carried out taking into account charge exchange, ion heating by electrons, ion-ion energy exchange and ion escape processes. A good agreement with experimental data was observed. According to the model, the processes of Pb ionization in EBIS at close to ultimate parameters (the electron beam current is 10 A and the electron energy is 10 keV, the trap capacity is about 10¹² e) by cooling with Ne ions were simulated.

The electron-beam method of multicharge ion production was suggested by E.D.Donets in 1967 [1]. The first attempt to create an Electron-Beam Ion Source (EBIS) theory was undertaken by R.Becker [2] and M.C.Vella in 1981 [3]. A more complete theory of the electron-beam method of multicharge ionization in an ion trap was created by the Livermore EBIT group (M.Levine, M.Penetrante, R.Marrs et al.) [4,5]. Based on these results, we present a simpler numerical model of multicharge ionization in EBIS. Simplifications follow from our previous papers [6,7]. The computer codes describing the Kryon-S experimental data can be used to predict EBIS basic parameters: charge state spectrum, ion-beam current and even ion temperatures.

According to the Livermore papers, main processes in the EBIS trap are the following:

-electron-impact ionization of ions,

-radiative recombination of ions,

-charge exchange between ions and neutral atoms,

-ion heating by an electron beam,

-ion-ion energy exchange,

-ion confinement in the trap,

-ion escape from the trap.

The processes were considerated in detail in previous parers [4,5,8,10].

We suppose that the ionization proceed by single steps:

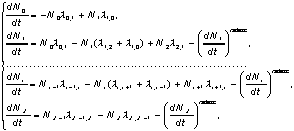
where N₀ .. N_Z are the ion and atom densities,

_0,1 , _1,2 , _i-1,i , _i,i+1 , _Z-1,Z are the ionization coefficients: j_e is the electron current density, _i,i+1 the ionization cross-section,

_1,0 , _2,1 , _i+1,i , _i,i-1 , _Z,Z-1 are the recombination and charge exchange coefficients:

_i,i-1=r +_p ,where , _r is the recombination cross-section, _p is the charge exchange cross-section, N₀ is the density of neutral atoms, <V_i> is the mean ion speed,

is the rate of ion diffusion escape from the trap.

The corresponding energy evolution is described by:

,

where kT_i is the ion temperature,

the rate of ion heating by the electron beam,

the rate of ion-ion energy exchange due to Coulomb collision,

the rate of the energy loss due to escaping ions.

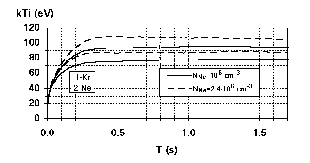
The dependences of Kr ion densities, electron beam compensation values, Kr ion temperatures on time at taking into account ionization, charge exchange, ion heating by the electron beam, ion energy exchange and ion escape processes were calculated in [10].

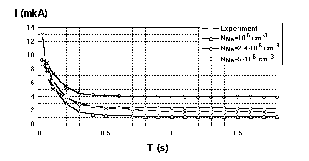
The experimental data of the Kr current at the EBIS Krion-S exit measured over an ion extraction time of 100 s and the calculated results obtained at j_e=1.7710²¹ 1/(cm^{2s), U}_e=710³ eV, N_Kr(0)=610⁹ cm^-3, r_p=0.015 cm, B=1.2 T, by cooling Kr ions with Ne ones.

The next step was to consider ion cooling processes. The method of ion cooling in EBIS was suggested by E.D. Donets and G.D. Shirkov [8]. Equation systems for charge and energy evolution created for Kr and Ne were solved simultaneously. We supposed that the concentration of Ne atoms (N⁰) in the electron beam is a constant [10].

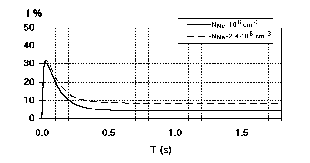
The calculated results for Kr ionization by cooling with Ne ions were compared with the experimental data of Kr current measurements at the EBIS Krion-S exit. The experimental current dependence on time was measured over an ion extraction time of 100 s. The best numerical approximation was obtained at the current density equals to j_e=1.7710²¹ 1/(cm^{2s), the electron energy U}_e=710³ eV, the start concentrations of Kr atoms N_Kr(0)=610⁹ cm^-3, the electron beam raius r_p=0.015 cm and the magnetic field induction B=1.2 T. The results for output current are shown in Fig. 1. The total numbers of ions, the values of beam compensation and the average ion temperatures corresponding to Fig. 1 are shown in Fig. 2, Fig. 3, Fig. 4.

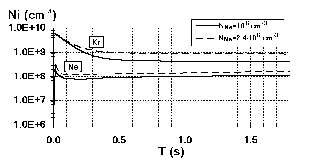
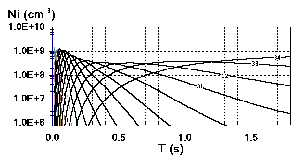
The time evolution of Kr ion densities at N_Ne=2.410⁶ cm^-3 corresponding to Fig. 1 is shown in Fig. 5.

The results were confirmed by an experimental observation of Kr higher charge state evolution at the LU-20 output when the EBIS Krion-S was installed on the linac pre-injector [9].

According to the model, the processes of Pb ionization in EBIS at close to ultimate parameters (the electron beam current is 10 A and the electron energy is 10 keV) were simulated. The electron gun for the source with the perveance equals to 3 A/V^3/2 at the cathode diameter of 3.4 mm, the cathode emission density of 111 A/cm², the first anode voltage of 22.3 kV and the second anode one of 10 kV can be produced in the firm "ISTOK" (Friasino, Moscow reg., Russia) [11]. After instalation of the e-gun in the EBIS, the value of DC current power at the EBIS collector will be equal to 100 kW.

To avoid problems due to collector heating a pulse regime of ionization is suggested. At the pulse duration is about t0.1 s the collector system can be cooled by water at the rate of flow is about G3 l/min. We suppose that the process of electron beam formation to reach the current density 200j_{e500 A/cm}² (as it takes place in Krion-S) won't be a very difficult problem. The time of ion extraction from the trap can be decreased from 100 s to 10 s. Therefore we carried out calculations of Pb atom ionization processes during 0.1 s at j_e=200 A/cm² and j_e=500 A/cm² by cooling the Pb ions with Ne ones and without one.

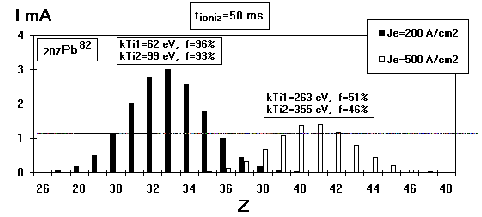
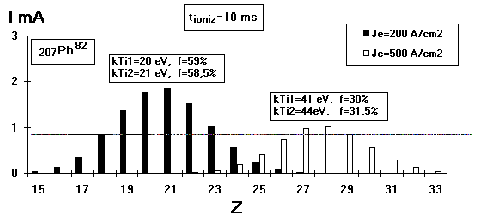
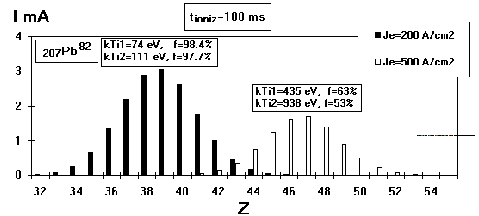
The results for output ion currents at the ion extraction time of 10 s for different ionization periods are shown in Fig. 6, Fig. 7, Fig. 8. In the calculations, the values of Pb ion currents for calculations with cooling are very close in amplitude to ones without cooling at the same ionization period. Therefore we present the ion currents for calculations with cooling only. The electron beam compensation values f and the average ion temperatures presented for both calculation types (with cooling- kTi1 and without one- kTi2) are shown above the currents.

The workable numerical model of EBIS has been created. The calculated results for Krion_S are close to the experimental ones. The model made more understandable the influence of different processes in the trap on the EBIS output parameters. It allows us to undertake some attempts to predict future results.

The authors are very grateful to Dr. E.D. Donets and Dr. G.D. Shirkov for their interest in the model and useful discussions. Thanks also to the SUN computer system manager S.A. Ivanovsky (JINR LNR) for providing our calculations.

[1] E.D. Donets, Soviet Invention #248860 of 16.03.67, Bull. OIPOTZ, #24, p.65 (1967 )

[2] R. Becker in Proc. of the 2-nd EBIS Workshop, Saclay-Orsay, p.185 (1981)

[3] M.C. Vella, Nucl. Instr. Meth. 187, p. 313 (1981)

[4] M.A.Levine et al. Phys. Scripta. V T22, p. 157 (1988)

[5] B.M.Penetrante et al. Phys. Rev. A 43, p. 4861 (1991)

[6] B. Sh. Bochev et al. JINR Preprint P5-11566 (1978)

[7] B. Sh. Bochev et al. JINR Preprint P7-11567 (1978)

[8] E.D. Donets, G.D. Shirkov, Soviet Invention #1225420 Bul. #44, p.69 (1989)

[9] V.P. Ovsyannikov, Proc. of the 1994 LINAC Conf. Tsukuba, Japan, p.384 (1994)

[10] I.V. Kalagin, V.P. Ovsyannikov, JINR Preprint E9-96-128 (1996)

[11] O. Kultashev, V. Ovsyannikov, Proc. of the 1994 LINAC Conf. Tsukuba, Japan, p.384 (1994)