We report the first studies of beam-induced microwave signals in the Damped Detuned Structure (DDS). The DDS is a 206 cell, nearly constant gradient structure, employing Gaussian detuning, and four symmetrically placed waveguide manifolds to damp the first-band dipole modes. We describe the manifold and output coupler design, bench measurements, and measurements with beam during the ASSET experiment. Dipole mode signals have been used to steer the beam to the structure center and minimize the wakefield kick.

The fundamental and dipole mode features of the DDS depicted in Fig. 1 have been described by Miller, et al. [1]. In this work we report on the manifold coupler design and bench-measurements, as well as measurements with beam. Our primary concerns are good coupling of the dipole modes through the manifolds, and the use of the microwave signals from the manifold for measurement of the beam position.

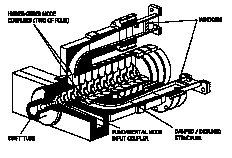
Fig. 1: Coupling of the HOM waveguide manifolds to WR62 waveguide for diagnostic measurements.

HOM Manifold Coupler Design and Measurement

To characterize the manifold-coupled higher-order modes (HOM) eleven Brillouin curves were determined from MAFIA frequency domain simulations, for the three lowest dipole modes, of strictly periodic structures having the dimensions of eleven representative cells [2]. The accuracy of the simulation for 5 such cells was tested by fabricating a short stack consisting of five cells and two half cells of like dimension and measuring the frequency of the various modes. Off axis E-field probes inserted into the cell portion of the end half cell were used to excite and detect dipole modes, while loop-type H-field probes in the manifolds were used to excite and detect manifold modes. Stacks were fabricated for cells 10,70,106,156, and 196, and the measured frequencies were found to agree well with the simulations. Measurements for cell 106 are compared to the computer simulations in Fig. 2.

Fig. 2: Theoretical and measured Brillouin curve for cell 106.

Of concern next was the design of an output assembly matched to the manifold over a broadband. This assembly was constrained to the space made available by the absence of manifold coupling to the first three and last three cells in the structure. The coupling of the 14.2 - 15.8 GHz dipole modes in the manifold depends on the local cutoff frequency of the manifold, which tapers slowly from 12.5 GHz at the upstream end to 14.0 GHz at the downstream end of the 1.8 m structure. We assumed that the taper in cutoff wavelength was sufficiently gradual that an assembly matched to a uniform structure with all cells identical would be adequate. The downstream assembly presented a significantly greater design challenge than the upstream assembly because of the proximity of the lower end of the frequency band to the manifold cutoff frequency (14.0 GHz). Both waveguide and coaxial coupling were considered for the upstream and downstream ends. Earlier cold tests performed on a uniform structure of eleven #106 cells indicated that waveguide coupling had the most promise to achieve bandwidth and reproducibility.

Two different output assembly designs were modeled on MAFIA and cold tested. Coupler & bend configurations were designed matching the manifold output to rectangular waveguides with cutoff frequencies of 12.5 and 13.3 GHz. The reflections of the two designs were similar, but the design using the 12.5 GHz cutoff waveguide was chosen because it is better suited to a small radius H bend.

An 11 cell stack of #203 cells with a coupler at each end was machined for cold test. MAFIA was used to design a coupler that was reasonably well matched at the middle and upper part of the band of interest. It was not possible to get a good match at the lower end. The coupler cold test pieces were made so that a series of cut and measure steps could be made starting with more metal than MAFIA predicted would be optimum.

Measurement of the coupler assembly reflection coefficient Gc relied on the fact that the match of a single unknown lossless network can be determined by measuring the complex reflection cofficient of a pair of identical unknown networks back-to-back separated by a variable length of transmission line. Thus a pair of coupler/mitre bend networks designed using MAFIA were separated by 8, 9, 10 and 11 identical #202 cells. The rf complex reflection measurements are made using an HP 8510C network analyser (NWA) in WR62 waveguide and tapers to the rectangular waveguide used in the coupler/mitre network.

At a given frequency, the locus of points in the complex reflection plane will lie on a circle. There will be four points, one from each measurement. A fifth point, located at the origin would always exist if the electrical spacing were such as to provide exact cancellation and thus a perfect match for this tandem configuration. The diameter of the resulting circle is the maximum possible reflection coefficient of the back-to-back networks. The magnitude of the reflection coefficient Gc of one coupler network (by itself as though terminated by the waveguide manifold matched in its own impedance) is related to the circle diameter D by

. (1)

It is not necessary to plot a circle for each frequency of interest. In theory, three points define the circle, its diameter, and ultimately the individual coupler Gc. Thus two reflection measurements (each with a different number of cells separating the two couplers) together with the assumed match condition will determine D according to

(2)

where |Gn| and fn are the respective magnitude and phase angles for the nth reflection measurement. The NWA data are read into a computer where D and Gc can be calculated for all frequency points from equations (1) and (2). The accuracy is reduced when the phase angle between the two vectors is less than 40_ or greater than 120_. The optimum is 60_.

The completed DDS with windows mounted was made available for time-limited NWA cold test measurements. With the fundamental-mode coupler-cell waveguides shorted, the structure may be regarded as an eight port network, and the complete S matrix with its 36 independent complex matrix elements can in principal be determined from network analyzer measurements. For a structure actually possessing the nominal symmetry, the number of independent elements reduces to nine, three of which relate to the dipole components and hence directly to the equivalent circuit. A set of measurements sufficient to determine one of the two dipole components was carried out, but the reduction of the data has not yet been completed. It is however clear even at this stage that detailed comparison with the equivalent circuit will require the introduction of resistive losses in the model.

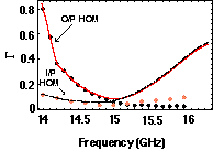
Fig. 3 Reflection coefficient Gc of the manifold output assemblies looking from the manifold into the mitre bend and the vacuum window, as inferred from bench measurements.

HOM Spectrum and Beam Position Measurement

Next, the prototype structure was installed on the Stanford Linear Collider beam-line, as part of the ASSET (Accelerator Structure SETup) experiment [3], at girder 2a of sector 2, a location where electron and positron bunches are available, at an energy of 1.2 GeV, bunch charge of 1-5nC, and variable orbit and bunch separation. The DDS output assemblies described above (ending in a vacuum window) were followed by WR62 terminated in a WR62 load with a 20dB (nominal) cross-guide coupler. In addition the fundamental mode input couplers were joined symmetrically via WR90 to a Tee, and tapered to WR62 followed by a 10dB side coupler and a WR62 load. The fundamental mode output ports were terminated in loads, with a 20dB cross-guide coupler on one load. Each of the ten output couplers fed a 17-meter length of 1/4" heliax carrying the microwave signals out of the accelerator housing to an instrumentation bench in the klystron gallery.

Several circuits were available in different configurations for examining the microwave signals excited by the beam in the structure. For spectrum acquisition we employed an HP8560A 50GHz spectrum analyzer (SA) connected via HPIB extender to a VXI crate and thence to the SLC's Solo Control Program (SCP). The SA acts as a receiver, using a two stage down-mixing scheme. In order to measure a spectrum the primary local oscillator frequency is swept continously over the desired frequency range. We also operated the spectrum analyzer on a fixed frequency to analyze directly the down-mixed signal after the first mixer stage. Together with a phase reference signal from a BPM this configuration allowed determination of amplitude and phase of selected individual dipole modes. For power detection over the full bandwidth we employed a crystal detector with acquisition to a 1 GHz VXI scope. An assortment of filters was on-hand to block out non-dipole bands, including a WR75 19 GHz low-pass filter, and several WR51 waveguide high-pass filters.

Fig. 4 shows the dipole mode spectrum observed at one of the horizontal HOM output couplers for a 1 mm vertical beam offset. A detailed part of that spectrum around 15 GHz is shown in Fig. 5 together with the predicted spectrum.

To employ this wakefield instrumentation to good effect we sought to locate the orbit of minimum wake-kick by steering the drive-bunch to a minimum of the induced 14-16 GHz microwave signals. We then checked the precision of this alignment by measuring the size of the residual wakefield kick with the second bunch and inferring the remaining offset of the drive bunch from the kick. Since this could be done at close bunch distances, where the wakefield is very strong, residual offsets of mm size were observable.

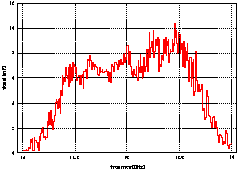
Fig. 4: Dipole mode spectrum observed at a horizontal HOM-output coupler, while the beam was steered to a vertical offset of 1.3 mm. Spectra were taken over a 30sec sweep time, with 2GHz span, and 1 MHz resolution bandwidth, at a beam rate of 50Hz.

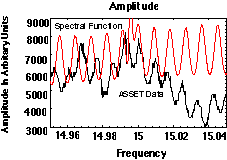
Fig. 5: Fine details of the observed spectrum, compared to theoretical predictions. The mode spacing is slightly smaller than predicted which is compatible with the observation of a somewhat delayed occurance of the recoherence peak in the ASSET-wakefield measurements [1].

In fact, three variations on this technique were used to align the beam with respect to the structure, based on dipole mode information. The slowest, but most detailed method involved stepping a single beam transversely across the structure, taking a complete spectrum at each step. Thereby one obtains a two-dimensional array of dipole mode power as a function of beam offset and frequency. Each frequency slice of that array is then fit to a parametrization of the form

(3)

The frequency of the modes can be related to an average cell number, i.e. a longitudinal position within the structure, using

(4)

which follows from the Gaussian distribution of the modes.

The essential information of such a power scan is contained in the fit parameter x₀(f(n)), which is the offset of the structure as a function of cell number with respect to the nominal beam orbit. In Fig. 6 minimum power positions obtained by this method are compared to data from mechanical measurements on a coordinate measuring machine.

The second alignment technique was simple, allowing fast beam steering, but less precise. The dipole mode signal is high-pass filtered to avoid contributions from the fundamental mode or low frequency noise and fed into a crystal detector. The resulting signal is roughly proportional to the averaged quadratic offsets of the beam in the individual cells. For an ideally straight structure the trajectory yielding a minimum of the crystal detector signal should also result in a minimal wakefield kick. For a structure with internal misalignments, however, the answer will be different since the effective wakefield kick is proportional to the averaged linear beam offset.

Fig. 6: Comparison of a structure-straightness measurement (lower curve) with the microwave-based determination of the electrical center. The 60 mm kink in the structure is reproduced in the minimum power-position measurement, though smeared out somewhat due to the fact that the modes extend over a fair number of cells.

Finally the most precise alignment method uses amplitude and phase detection of two different modes, where one was chosen at the upstream end and one at the downstream end of the structure. In this method, the spectrum analyzer was switched quickly back and forth between two fixed frequencies. When the beam passes the centre of the structure transversally the phase of the dipole mode signal flips by 180_. Since this phase switch occurs rather rapidly as a function of beam position the phase measurement provides a more precise position measurement than the mode amplitude. A detailed analysis of the residual wakefield kicks is in preparation and will be published in the near future.

Work supported by DOE DE-FG03-93ER40759 and DE-AC03-76SF00515.

[1] R.H. Miller et al., A Damped Detuned Structure for the Next Linear Collider (paper THPO2, these proceedings)

[2] K. Ko et al., 16th IEEE Particle Accelerator Conference, Dallas, TX 1995

[3] C. Adolphsen, et al., Proc. LINAC94, p.481.