High-intensity, high-energy proton beams are required in various fields of science and industry, including pulsed-spallation neutron experiments, nuclear-physics experiments, and nuclear-waste transmutation. We have various possible accelerator schemes for these purposes. The advantages and disadvantages of the parameter choices are summarized while emphasizing the importance of understanding the halo-formation mechanisms in order to settle various controversial issues. The beam current to be accelerated is actually limited by the amount of beam loss, which is critically dependent upon the amount of beam halo, both longitudinal and transverse. The optimum design is also dependent upon the future performances of the key components, such as high-intensity, low-emittance ion sources. Thus, we should concentrate our efforts on the development of these components in order to realize these machines. Some examples of the efforts being made in this direction are presented.

The scope of this paper is to list various topical controversial issues concerning the design of high-intensity (typically more than 0.1 mA), high-energy (more than 1 GeV, but less than several 10 GeV) proton accelerators, and to hopefully present possible solutions, or to propose directions for further research and development. Examples of these machines are listed in Table 1 [1-8].

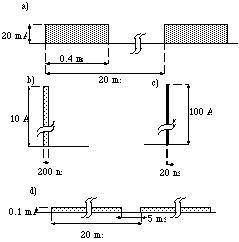
The optimum design of an accelerator is dependent upon its detailed specifications. The specifications for intensity and energy are still insufficient for optimizing the design. Other important factors are the time structure and emittance of the beam. Typical examples of useful time structures are shown in Fig. 1 ( a few 100 ns, a few 10 ns, CW or nearly CW). The beam as shown in Fig. 1 b) is required for spallation neutron experiments [10] with a high energy resolution, based upon the time-of-flight method. That shown in Fig. 1 c) is useful for muon spin rotation/resonance/relaxation experiments [11] in order to study mainly material science. An average current as high as possible is required for nuclear-waste transmutation/incineration [12], while a long-pulse or nearly CW beam is usually requested for nuclear-physics experiments(Fig. 1 d) [13]). A relatively low emittance (typically an unnormalized 90% emittance of around 2 p mm·mrad) is necessary for the latter.

The beam represented by Fig. 1 b) and c) ( a peak current of a few 10 A) cannot be obtained directly from an ion source, the maximum peak beam current of which is on the order of 100 mA. This is the reason why we need a synchrotron ring with a revolution time of a few 100 ns. A typical schematic accelerator complex thus comprises an injector linac and a synchrotron ring. The highest possible beam current will be filled up in the ring, and will then be fast-extracted. The ring is used as a compressor with a pulse length equivalent to its revolution time in this case. Additional bunch compression with a bunch rotation is possible down to a few 10 ns (Fig. 1 c)) in a ring by applying a high voltage [9,14].

On the other hand, if what one needs is only a high average current, for example a few 100 mA, a unique solution would be a CW proton linac. However, if the necessary average current is much lower than the possible peak beam current in a linac, the CW proton linac scheme is extremely expensive. The best choice is again the accelerator complex comprising a linac and a ring, where the ring is used as a stretcher [9,14]. The beam is slowly extracted from the ring in this case. If the necessary energy exceeds around 3 GeV, one more ring should be built as in the case of JHP [7].

Among the various technical problems involved in building high-energy, high-intensity proton accelerators, beam loss is among the most crucial. It should be realized that the beam current to be accelerated is really limited by the amount of beam loss. Beam loss in the high-energy region not only gives rise to a radiation-shielding problem, but also to the radioactivity of the machine itself. The radioactivity should be reduced to a certain level which would allow hands-on maintenance (at worst around 5 nA/m/GeV [15]; hopefully, much less). Accidentally, this level of the radiation can be shielded by a reasonable amount of concrete down to an environmentally allowable level.

At present it is believed that the behavior of the beam core can be well controlled during the injection, acceleration, and extraction processes. Also, we perhaps understand some mechanism concerning the growth of rms- or 90%- emittance during the acceleration in linacs. However, beam loss at a level 10-7 /m/GeV arises from the beam halo, the generation mechanism of which has not yet been fully understood. The difficulty to reliably estimate the beam loss gives rise to controversy for determining the optimum design.

Table 1

Examples of the operational and planned high-intensity, high-energy proton accelerators. The first three columns show the operational machines, while the others are planned. The MMF linac is partly operational.

ISIS LAMPF/PSR AGS MMF-INR ESS ORSNS JHP-Booster JHP-50

Energy (GeV) 0.8 0.8 24 0.6 1.33 1 3 50

Injection Energy (GeV) 0.07 0.8 1.5 0.6 1.33 1 0.2 3

Repetition Rate (Hz) 50 20 0.56 100 50 60 25 0.3

Average Current (mA) 200 70 5 500 3,800 1,000 200 10

Total Power (MW) 0.16 0.056 0.12 0.3 5 1 0.6 0.5

Ref. [1] [2] [3] [4] [5] [6] [7,8] [7,8]

For this reason, considerable efforts [16] have been devoted to a theoretical study of the beam-halo generation mechanism. For example, it was shown that the halo is formed from particles interacting with the core oscillation or breathing [17]. A recent computer-simulation result [18] has shown that a beam with a hard core eventually results in a soft beam during the course of 1.3-GeV acceleration in the ESS proton linac [5], although no error in the alignment or accelerating field is included. Since a halo comprising a fraction of 10-4 of the total beam current grows far beyond the Gaussian tail, these kinds of halos can not be recognized by watching only the rms-emittance growth.

It is quite common that non-linear phenomena are strongly influenced by the error field [19], such as a deviation from the ideal focusing or accelerating system in the present case. The information which is really necessary to design high-intensity, high-energy proton accelerators is quantitative in the form of tolerance, by which the halo formation can be minimized. Unfortunately, it is still impossible to obtain quantitative information, since this kind of simulation presently consumes a tremendous amount of computing time.

Until a quantitatively reliable estimate becomes possible, we have no other way than to follow the design principle to minimize the rms-emittance growth, keeping the difference in mind. Nevertheless, the principle seems to be qualitatively applicable to minimizing the halo formation from the general characteristics of non-linear phenomena. It has been theoretically known that emittance growth arises due to the following mechanisms: the charge-redistribution from the given one to a uniform one [20], the energy transfer among the longitudinal and transverse oscillations [21], rms-mismatching [22] and structure resonances [22]. In particular, the latter two mechanisms imply the effect of a deviation from the ideal focusing and/or accelerating systems within the framework of non-linear space charge dynamics, which is perhaps common in both halo-formation and rms-emittace growth.

There are two ways of obtaining MW proton beams with a ms pulse duration: combining a full-energy linac and a storage ring, or combining a low-energy linac and a rapid-cycling synchrotron (RCS). However, if the specification exceeds around 5 MW, or requires upgradability, the former option is only a choice regarding the space charge limit in a ring and a relatively short stay of the beam in the ring. By adding a relatively inexpensive storage ring (compared with RCS), and by increasing the pulse length of a linac, one can double the power in this case. The RCS option requires a larger number of powerful RF cavities in order to rapidly accelerate the beam, and ceramic vacuum chambers with RF shields to eliminate any eddy current which would otherwise be induced by rapidly changing magnetic fields.

However, if the beam current is limited by the beam loss during the injection process, the lower injection energy has some advantages, since the radioactivity is roughly proportional to the beam energy. A beam loss of approximately an order of magnitude higher will be allowed in 200-MeV injection than in 1.334-GeV injection. One may partly attribute the success of ISIS [1] to its low injection energy (70 MeV) to RCS. Since the beam-loss mechanism in a ring is another, or more difficult problem, to understand, it is not yet a settled problem which is more advantageous between the two options if the beam power does not exceed a few MW.

It should be appreciated that magnet lattices have been devised in order to realize a negative, or extremely small, momentum compaction factor [23], by which no transition needs be crossed during acceleration. The beam loss otherwise arising from the transition crossing will be drastically eliminated. This kind of lattice has been extensively and carefully tested in Super ACO [24], showing the validity of the theory.

If beam-halo formation is unavoidable in a linac, and if high-energy injection is necessary regarding the space-charge limit, a series of halo collimators [5] should be installed, particularly in longitudinal phase space, in order to eliminate the halo, which would otherwise result in a beam loss during injection. The longitudinal collimators must be located in the high-dispersion, (hopefully) low-b region. In any case, the beam loss should be localized by the halo collimators.

If one has to inject the beam into the ring for an order of several hundred ms or turns, it should comprise negative hydrogen ions. In contrast to positive ions negative ones can be injected with the same condition as that of circulating positive ions until the time is limited by other effects, such as the space-charge limit and/or beam instabilities and/or Coulomb scattering in a charge-exchange foil. At present no ion source simultaneouly meets all the requirements (typically, a peak current of several 10 mA, a normalized 90% emittance of 1 p mm·mrad, a pulse length of several 100 ms, a repetition of several 10 Hz, without or with a very small amount of Cs) for MW machines. It is, again, very difficult to predict what will be the current limit of a single negative hydrogen ion source in the future. This is another reason for controversy regarding choosing parameters. In any case, the highest-possible peak beam current (of course, stably obtainable) of negative hydrogen ions with a reasonably low emittance ( a normalized 90%-emittance below 1p mm·mrad) should be improved by carrying a more extensive study and developing ion sources.

At first, the volume-production type of ion sources was considered to be advantageous regarding not only high brightness, but also the elimination of Cs vapors. There are some indications that the Cs vapors reduce the discharge limit, possibly being harmful to the high-field operation of the following RFQ. However, a source without Cs has produced only a peak current of 16 mA with a normalized 90% emittance of 0.5 p mm·mrad [25]. Since it has been indicated that the introduction of a very small amount of Cs vapor drastically (approximately by a factor three) improves the beam current, even in the volume-production type [26], it is important to empirically test the effect of this amount of Cs on the discharge limit in the RFQ. It seems to be quite possible that a small amount of Cs vapor is practically harmless.

On the other hand, if a beam current of negative hydrogen ions continues to be by an order of magnitude smaller than the proton beam for the same emittance, proton injection would be another choice for a 0.1-MW machine.

The frequency is another important parameter which needs to be determined. Conventional proton linacs have been using around 200 MHz for the drift-tube linac (DTL). Most of the recently proposed designs have suggested the use of a higher frequency (300 MHz to 400 MHz) for the following reasons.

If one doubles the frequency, it is possible to halve the number of particles per bunch. In addition, the focusing period becomes more frequent both longitudinally and transversely. As a result the space-charge effect would be approximately halved. Computer simulations have been attempted in order to confirm the above expectation. For a fair comparison between the low- and high-frequency schemes we need optimum designs for both schemes, although we have no reliable algorism which can generate the optimum parameters for reducing the emittance growth and halo formation. In spite of this difficulty, some computer simulations indicate that the higher frequency scheme is more advantageous [27].

The best advantage of the higher-frequency scheme is the use of klystrons, which are the most powerful and stable rf power sources, and having mature engineering techniques.

It is difficult to increase the frequency of the low-energy front DTL further, if one wishes to contain quadrupole electromagnets in drift tubes in order to keep the flexibilty for the future upgrade of the peak beam current. This is the reason why we choose 324-MHz DTL to accelerate the beam from 3 MeV.

An RFQ linac [28] is an ideal device, in which both longitudinal and transverse focusings are incorporated together with the ideal adiabatic bunching. Therefore, it is preferable to use the RFQ up to the highest-possible energy [29]. However, the field of a conventional four-vane RFQ is difficult to stabilize if the RFQ is elongated over four wavelengths in order to accelerate the beam up to typically 3 MeV. The dispersion curve [30] of the RFQ clearly shows the reason for the difficulty in field stabilization. The dipole (TE11n) mode is easily mixed with the accelerating quadrupole (TE210) mode, since the frequencies of these modes become close together. Although a Vane-Coupling Ring (VCR) [31] could solve this problem, by increasing the frequencies of the dipole modes, it cannot be used for a high-duty machine, because it is difficult to water-cool. The p-mode Stabilizing Loop (PISL) [32] is easy to water-cool while keeping similar beam stabilizing characteristics to that of the VCR. Another solution may be to use a four-rod RFQ [33], for which we should again find a special water-cooling device. Together with a recent further development for elongating the RFQ [34], it has been proposed to use an RFQ of up to 8 MeV.

However, the transition energy from an RFQ to a DTL should be carefully chosen by taking into account the detailed design of the medium-energy transport for matching the beam both longitudinally and transversely. In addition we should find the optimum space for installing the chopper. In the ESS design the 5-MeV RFQ is separated into two parts, between which the chopper is located at 2 MeV [5]. The beams of the two RFQ's are funneled together into the DTL by choosing the frequency of the two RFQ's as one half of that of the DTL. In this case one should find some means to minimize the emittance growth and halo formation during the funneling process.

Before discussing the DTL it is useful to introduce the concept of a separated DTL(SDTL) [35], in which the focusing magnets conventionally contained in the drift tubes are located outside. Since the drift tubes become free from the constraint of containing the quadrupole magnets, the shunt impedance of the SDTL can be optimized even further. In addition, the drift tubes become significantly easier to fabricate by removing the magnets, resulting in a drastic reduction in the cost of the DTL. It is, however, controversial what should be the transition energy from the conventional DTL to the SDTL. Needless to say, the focusing quality of the SDTL is inferior to that of the conventional DTL (the focusing period of the SDTL is longer than that of the DTL). If one wishes to have a better quality in order to overcome various space-charge effects, one should choose a higher transition energy. We are at present assuming a transition energy of 55 MeV for the JHP.

There may be several versions of SDTL: a Bridge-Coupled DTL in narrow [36] and wide meanings and a Coupled-Cavity DTL [37]. The choice of a specific version requires a significant trade-off study, including the detailed engineering design.

A discussion concerning the choice of the high b structure is omitted here, since it is detailed in Ref. [38]. However, the choice is again dependent upon understanding the halo-formation mechanism. The transverse electric kick [39] existing in the side-coupled structure (SCS) gives rise to a slight amount of continuous transverse oscillation of the beam core, possibly resulting in halo formation. We have not yet obtained any reliable quantitative conclusion for this possiblity. If it is really significant, the annular-ring coupled structure (ACS) is the one which has the balanced characteristics of both the shunt impedance and the field symmetry [40]. The importance of the field stability, in particular, against the heavy beam loading stressed in Ref. [39] is justified by a recent study [41].

It is another issue as to at what energy one should make the frequency jump from low frequency to high frequency, or any other abrupt transition, if necessary. The frequency jump at lower energy is preferable from a power-saving point of view. In addition, the beam loss arising from the frequency jump at a lower energy can be managed more easily than that at a higher energy. However, the ratio of the acceptance to the emittance is higher in the case of a high-energy frequency jump due to adiabatic damping, favoring the high-energy option from the beam-loss viewpoint [29]. It should also be noted that a low-energy, high-frequency structure is difficult to fabricate, particularly to equip it with water-cooling channels for a high-duty machine.

It  appears to be energy-saving to use a super-conducting cavity (SCC) structure. This is true only if the beam pulse is longer than a few ms, since the filling time of the typical super-conducting structure is of several 100 ms under practically "reasonable" beam loading. In a long beam-pulse machine the SCC approach (see also Ref. [42]) implies the following additional advantages over the normal-conducting cavity (NCC) scheme (sometimes referred to as room-temperature cavity). First of all, we can use large bore radii, which are unpractical in an NCC scheme due to the increase in power dissipation. This is advantageous regarding a reduction in the beam loss. (This is only true if the present theories concerning the halo formation correctly predict the behavior of the halo, which is characterized by a saturation in the halo-envelope development. Otherwise, the large bore radii may give rise to a delay in beam loss to the high-energy region, resulting in more radioactivity.) Second, we can use a higher field gradient, typically 5 MV/m and hopefully 40 MV/m, than that of the NCC (typically around 1 MV/m for CW). The former is determined by the power capability through input couplers or by the refrigerator power consumption, while the latter is usually determined by optimizing both the capital and operational costs. Since the RF power becomes expensive both capitally and operationally as the pulse is elongated [38], the total shunt impedance must be increased by elongating the NCC's, that is, by decreasing the field gradient. Third, the stored energy in the SCC system is extremely higher, being immune against any variation of the beam loading [43,44], as in the case of beam chopping.

On the other hand, the amplitude-phase control is more difficult than the NCC scheme, since the beam loading is extremely heavier than the power dissipation. It is noted that the tolerance of the amplitude-phase control in proton accelerators is much more severe than in electron accelerators. It will also be necessary to carefully investigate the radiation-damage effect on the superconductivity, although there is no evidence that it is fatal.

If one uses the SCC, it is possible to use a low peak current in order to ease the space-charge problem. However, if one wishes to inject the beam into a ring, there is a limit in the number of turns by which higher-order resonances can be excited. The number can be significantly reduced by the tune spread due to the space-charge effect, being the same order of magnitude as that of the typical filling time, as mentioned above. In addition, the beam instability and the Coulomb scattering by the charge-stripping foil limit the number of possible turns for injection. A careful study is still necessary in order to settle the problem of whether the SCC scheme is really advantageous if the injection to a ring is required. The SCC scheme is definitely useful for a multi-purpose facility, for example, including multi-storage rings, nuclear-waste transmutation test area and others, like the new version of the JAERI project [45] (the multi-storage rings are not included in this project).

There are two kinds of longitudinal capture schemes in a ring: one is an adiabatic capture [46], while the other uses a chopper. The chopper system should be more advantageous than the former regarding beam loss during the capture process. However, we have no established chopping scheme for the several-MeV RFQ, although there are some proposed schemes. For example, a series of two subsequent RFQ's will be used in the ESS linac with a chopper in between the two RFQ's. For the JHP linac a low-Q deflecting cavity is under investigation with the same frequency as those of the RFQ and DTL, in between which the chopper is located [47]. It is most important to eliminate the beam during the beam-chopped period rather than the nominal values of the rise and falling time of the chopper.

Other important features required for high-intensity proton rings are painting in the ring acceptance, both longitudinally and transversely, in order to suppress the space-charge effect. The bunching factor should be decreased by some means, such as 2nd-harmonics cavities [48] or barrier cavities [49].

After LAMPF/PSR and ISIS were built, extensive studies were performed in order to improve the design of high-intensity, high-energy proton accelerators. The experience obtained by operating these accelerators has been playing an important role in the studies. However, since no such machine has been built afterwards, we have had only a few chances to test the new theories. This is the main reason why we have so many controversial issues. It is really necessary to build a new machine with an improved design on the basis obtained from the LAMPF/ISIS experience and others.

The author would like to express thanks to T. Kato, who is actually designing the JHP linac using his newly developed computer-simulation program. The present paper is based upon a discussion with him. The author would also like to thank K. Bongardt for his many instructive suggestions. Greatly acknowledged is the information given by R. A. Jameson, particularly regarding halo-formation theories.

[1] I.K. Gardner, "ISIS Status Report". Proc. EPAC-94, p3 (1994)

[2] R.J. Macek, "Progress on the PSR/LANSCE Upgrade". Proc. ICANS-XIII, PSI 95-02, p44 (1995)

[3] W. T. Weng, private communication

[4] L.V. Kravchuk, "Moscow Meson Factory Linac for the Pulsed Neutron Source". Proc. ICANS-XIII, PSI 95-02, p724 (1995)

[5] I.K. Gardner, H. Lengeler, and G.H. Rees, "Outline Design of the European Spallation Neutron Source". ESS 95-30-M (1995)

[6] B. Appleton, "Status of the Oak Ridge Spallation Neutron Source (ORSNS) Projet". Proc. ICANS XIII, PSI 95-02, p814 (1995)

[7] Y. Mori et al.,"Outline of JHP Synchrotron Design". Proc. 10th Symp. Accel. Sci. Tech., p454 (1995)

[8] M. Furusaka and H. Ikeda, "Current Status of JHP N-arena". Proc. ICANS-XIII, PSI 95-02, p836 (1995)

[9] M. Kihara, "Present Status of the Japanese Hadron Project". Part. Accel. 32, 1 (1990)

[10] H. Klein, "Spallation Neutron Sources". Proc. 1994 Linac Conf., Tsukuba, p322 (1994) and a series of ICANS (International Collaboration on Advanced Neutron Sources) Proceedings

[11] K. Nagamine, "Japanese Hadron Facility Plans and Future mSR". Hyperfine Interactions 65, p1149 (1990)

[12] M. Mizumoto, "Accelerators for Nuclear Waste Transmutation". Proc. 1994 Linac Conf., Tsukuba, p317 (1994)

[13] For example, "The Physics and a Plan for a 45 GeV Facility that Extends the High-Intensity Capability in Nuclear and Particle Physics". LA-10720-MS (1986)

[14] G.H. Rees, "Theory and Design Aspects of the 1 GeV Proton Compressor Ring for Pulsed Beams of Spallation Neutrons and Muons". INS-J-172 (1988)

[15] R.A. Jameson, "High Intensity Linear Acceleerator Development Topics for Panel Discussion on Nuclear Energy Research and Accelerators - Future Prospects". Proc. 2nd Int. Symp. Advanced Nuclear Energy Research, Mito, p163 (1990)

[16] For example, R.L. Gluckstern, "Survey of Halo Formation Studies in High Intensity Proton Linacs". Proc. 1994 Linac Conf., Tsukuba, p333 (1994), and J. M. Lagniel, "Halos and Chaos in Space-Charge Dominated Beams". Proc. EPAC-96, WEY01A (1996)

[17] For example, R.A. Jameson, "Beam Halo from Collective Core/Single-Particle Interactions". Los Alamos Report LA-UR-93-1209 (1993)

[18] K. Bongardt and M. Pabst, "Accelerator Physics of High Intensity Proton Linacs". Proc. EPAC-96, TUY02A (1996)

[19] For example, A.J. Lichtenberg and M.A. Lieberman, "Regular and Stochastic Motion". Springer-Verlag (1983)

[20] For example, T.P. Wangler et al., "Relation between Field Energy and RMS Emittance in Intense Particle Beams". IEEE Trans. Nucl. Sci. NS-32, p2196 (1985)

[21] R.A. Jameson, "Equipartitioning in Linear Accelerators". Proc. 1981 Linac Conf., Los Alamos, p125 (1982)

[22] For example, M. Reiser, "Theory and Design of Charge Particle Beams", John Willy & Sons (1994)

[23] For example, M. K. Craddock et al., "High Transition Energy Magnet Lattices", IEEE Trans. Nucl. Sci. NS-32 (1985)

[24] A. Nadji et al., "Experiments with Low and Negative Momentum Compaction Factor with Super-ACO". Proc. EPAC-96, WEP090G (1996)

[25] A. Ueno, "Beam Test of the Preinjector and the 3 MeV H- RFQ with a New Field Stabilizer PISL". this conference

[26] Y. Mori et al., Nucl. Instr. Meth. A301 , 1 (1991)

[27] T. Kato, "Beam Dynamics in Proton Linear Accelerators". JHP-28, p5 (1995) (in Japanese)

[28] I.M. Kapchinskii and V.A. Teplyakov, Prib. Tekh. Eksp. No.2, 19 (1970), No.4 , 19 (1970)

[29] Y. Yamazaki and M. Kihara, "Development of the High Intensity Proton Linac for the Japanese Hadron Project". Proc. 1990 Linear Accel. Conf., p543 (1990)

[30] A. Ueno and Y. Yamazaki, "RF Field Measurement of a Four-Vane Type RFQ with PISLs". Proc. 1992 Linac Conf., Ottawa, p713 (1992)

[31] H. R. Schneider and H. Lancaster, IEEE Trans. Nucl. Sci. NS-30, p3007 (1983)

[32] A. Ueno and Y. Yamazaki, "New Field Stabilization Method of a Four-Vane Type RFQ". Nucl. Instr. Meth. A300, 15 (1990)

[33] R. Kazimi et al., "Operation of a 473 MHz Four-Rod Cavity RFQ". Proc. 1992 Linac Conf., Ottawa, p317 (1992)

[34] L.M. Young, "An 8-Meter-Long Coupled Cavity RFQ Linac". Proc. 1994 Int. Linac Conf., Tsukuba, p178 (1994)

[35] T. Kato, "Proposal of a Separated-Type Proton Drift Tube Linac for Medium-Energy Structure". KEK Report 92-10 (1992)

[36] D.P. Rusthoi, "A High-Intensity, Low-Beam-Loss 1.5 GeV Proton Linac Reference Design for JAERI Transmutation Technology". LA-CP-93-178 (1993)

[37] J.H. Billen et al., "A New RF Structure for Intermediate-Velocity Particles". Proc. 1994 Int. Linac Conf., Tsukuba, p341 (1994)

[38] Y. Yamazaki, "Recent Technological Development of Accelerating Structures". Proc. 1992 Linear Accel. Conf., p580 (1992)

[39] T. Kageyama et al., "Developmnet of Annular Coupled Structure". Proc. 1992 Linear Accel. Conf., p456 (1992)

[40] T. Kageyama et al., "A New Annular-Coupled Structure Suppressing Higher Order Modes' Mixing with the '/2 Coupling Mode". Part. Accel. 32, 33(1990)

[41] Y. Senichev, "The Transient Effect in High Intensity Proton Linear Accelerator". Part. Accel. 51 (1995)

[42] R.A. Jameson, "Comparison of SC and Room Temperature High Intensity Linacs". Proc. EPAC-96, WEX03A (1996)

[43] Y. Yamazaki and T. Kageyama, "A Three-Cavity System which Suppresses the Coupled-Bunch Instability Associated with the Accelerating Mode". Part. Accel. 44, 107 (1994)

[44] Y. Yamazaki et al., "An Accelerator Resonantly Coupled with an Energy Storage (ARES) for the KEKB". Proc. 1995 PAC and ICHEA, p1503 (1995)

[45] M. Mizumoto et al., "Development of a High Intensity Proton Accelerator". Proceedings of 2nd International Conference on Accelerator Driven Transmutation Technologies and Applications, 2-7 June 1996, Kalmar, Sweden

[46] C.G. Lilliequist and K.R. Symon, "Deviations from Adiabatic Behavior during Capture of Particles into an RF Bucket". MURA Report No. 491 (1959)

[47] T. Kato, "New Design of an RF Beam Chopper". Proc. 7th Symp. Accel. Sci. Tech., p228 (1989)

[48] C.R. Prior, "Studies of Dual Harmonic Acceleration in ISIS". Proc. ICANS-XII, A11(1993)

[49] M. Blaskiewicz, "Barrier Cavity Longitudinal Dynamics". AGS/AD/Tech. Note No. 409 (1995)