We examine ion linac designs that start
with a high-energy radio-frequency quadrupole (RFQ) followed by
either a drift-tube linac (DTL) or a coupled-cavity drift-tube
linac (CCDTL). For high energies, a conventional CCL follows the
CCDTL. High RFQ output energy allows tailoring the transverse
and longitudinal focusing strengths to match into the following
structure. When the RFQ beam enters a higher-frequency structure,
the DTL or CCDTL starts with a low accelerating gradient and large
negative synchronous phase. The gradient and phase both ramp up
gradually to higher values. Other changes later in the machine
are also gradual. Beam-dynamics simulations show that these linacs
require no separate matching sections. Applications include a
cw 100-mA H+ beam from a 350-MHz, 6.7-MeV RFQ injecting
a 700-MHz CCDTL and CCL; a 7% duty 28-mA H beam from
a 402.5-MHz, RFQ and DTL injecting 805-MHz structures; a cw 135-mA
D+ beam produced by a 175-MHz, 8-MeV RFQ and DTL; and
a 2.4% duty, 80-mA H+ beam using a 433-MHz 10-MeV RFQ
and a 1300-MHz CCDTL. The machines take advantage of the considerable
flexibility of the CCDTL. Designs can use a variety of different
transverse focusing lattices. Use of two coupling-cavity orientations
permits a constant period even when the number of drift tubes
per cavity changes along the linac.
For the past two years, we have been incorporating the CCDTL [] structure into conceptual designs of several high-intensity ion accelerators. We have concentrated on designs that require no separate matching sections between linac sections with different rf structures. Table 1 lists parameters for four applications. Of all the designs, the Accelerator for Production of Tritium (APT) is in the most advanced state of development. We are now building the 6.7-MeV (RFQ) [,] as part of a low-energy demonstration facility for APT.
Other accelerator designs we have studied differ in details from the APT, but follow similar design strategies. Work on the National Spallation Neutron Source (NSNS) has just begun []. This conceptual design study is a collaborative effort by five US national laboratories (ORNL, LBNL, BNL, ANL, and LANL). Recent design studies [] for the International Fusion Materials Irradiation Facility (IFMIF) accelerator do not include a CCDTL. However, the Los Alamos design in Ref. 5 uses matching strategies at the RFQ-to-DTL interface similar to those developed for the CCDTL. For medical isotope production, our design concept [] is a compact machine consisting of an RFQ and CCDTL.
These designs offer advantages that stem from four
key features: 1) a uniform focusing lattice throughout the major
portion of the linac, 2) external location and separate mechanical
support of the electromagnetic quadrupole magnets, 3) flexible
modular physics design and mechanical implementation, and 4) compact,
high-frequency structures. These features help to reduce beam
loss and, hence, also reduce potential radioactivation of the
structure. They should result in easy alignment, fast serviceability,
and high beam availability.
In this paper, the APT design serves to illustrate the techniques that help achieve smooth focusing and acceleration throughout the linac. We mention features of the beam-dynamics, rf-structure, and mechanical engineering design. Parameters listed for the APT linac in Table 1 correspond to the reference design of a room-temperature copper structure. Several other papers [,,,,] at this conference provide more technical details of this work.
The APT project includes a superconducting option
[] for the high-energy portion of the machine. The physics and
engineering design of the superconducting (SC) components is approaching
the maturity of the room-temperature reference design. Work is
now in progress on an integrated design that will use room-temperature
structures discussed in this paper up to about 217 MeV proton
energy. The SC linac consists of two constant-length FODO lattices.
The first one uses = 0.64 cavities and the second uses = 0.82
cavities. Transitions between linac sections do not require separate
matching sections. Careful attention to maintaining constant average
focusing strength through the transitions provides the match.
Our recent RFQ designs employ several features near the RFQ exit that help match the beam into the following structure. These include:
In order to apply the technique of reducing the transverse focusing strength, the final RFQ energy must be high compared to most previous RFQ designs. For example, the APT RFQ energy is about 6.7 MeV, which requires a long (8 meter) structure described in Ref. 2 and 3. In the design now under construction we were able to reduce the transverse, zero-current phase advance per period to about 20 degrees. The focusing period is four times longer in the 700-MHz CCDTL than in the 350-MHz RFQ. Thus, 20 degrees/period in the RFQ provides a smooth transition to 80 degrees/period in the CCDTL.
The transition cell described by K. Crandall [] eliminates
energy gain or loss in the following radial matching section.
This feature frees the designer to choose the length of the radial
matching section for the transverse match into the CCDTL magnetic
quadrupole channel. The increased longitudinal focusing achieved
by tailoring the vane-tip modulation reduces the phase width of
the exit beam. The shorter bunch eases capture of the beam in
the CCDTL.
Table 1. Accelerator Design Summary for a Few Applications
| Application | ||||
| Ion Species | ||||
| Peak Beam Current (mA) | ||||
| Duty factor | ||||
| Frequency (MHz) | ||||
| Injection/Final Energy (MeV) | ||||
| Length (m) | ||||
| Peak Structure Power (MW) | ||||
| Peak Beam Power (MW) | ||||
| Peak Surface Electric Field | ||||
| Structures Types | ||||
| Structure Frequencies (MHz) | ||||
| Final Energy (MeV) | ||||
| Cavity E0 (MV/m) | ||||
| Quadrupole Focusing Lattice | ||||
| Transverse Focusing Period | ||||
| Total Length (m) | ||||
| Radial Aperture (cm) | ||||
| Peak Surface Electric Field | ||||
| Peak Structure Power (MW) | ||||
| Peak Beam Power (MW) | ||||
| Number of RF Modules | ||||
| Klystron Power (MW) | ||||
| Klystrons/Module | ||||
*Estimate based upon current design parameters.

Figure 1 shows the first few focusing periods of the CCDTL structure that starts at 6.7 MeV. The gradual ramp in synchronous phase s starts at 60 ensuring a large enough rf "bucket" to capture 100% of the beam. (The term synchronous phase here refers to the design particle's average phase with respect to the rf-field peak in a 2-gap cavity. For a given cavity with cells designed for fixed , the true s would be 90.) The ramp in s eventually stops at 30. However, the first two cavities are exceptions. The first CCDTL cavity has s = 90 and a larger field amplitude than subsequent cavities. The second cavity operates at s = 30. This scheme compensates for the lack of any longitudinal focusing from the RFQ transition cell to the first CCDTL cavity. Reference 8 provides additional numerical details. Unlike conventional matching sections, these matching cavities are an integral part of the CCDTL structure described in the next section. Their phases and amplitudes are locked to the subsequent cavities through side coupling cavities. The relative longitudinal spacing between cavities determines the synchronous phase.
Matching the CCDTL to the average longitudinal focusing strength in the RFQ results in a low accelerating gradient E0. Both the phase and the accelerating field vary gradually as the beam energy increases. By 12 MeV the synchronous phase has reached about 40, and E0 has increased from 1.68 to 2.2 MV/m. Figure 4 of Ref. 7 shows how E0 varies throughout the entire accelerator.
The first four quadrupole lenses in the CCDTL match
the beam from the RFQ in both transverse planes. In Figure 1,
the quadrupole magnets are approximately centered in the spaces
between cavities. Including a beam-line valve before the first
cavity required a modified layout. The structure's flexibility
allowed a redesign in which all the cavities were shifted downstream
with respect to the fixed magnets.
The first 24 accelerating cavities, up to a beam energy of 8.1 MeV, are single-drift-tube cavities of length 3/2. The drift spaces between cavities are 5/2 long. Electromagnetic quadrupole (EMQ) singlets and diagnostic elements occupy the drift space. A transverse focusing period consists of a cavity, a focusing EMQ, another cavity, and a defocusing EMQ. This FODO lattice has a period of 8 at 700 MHz. For the low particle velocity ( = 0.12 to 0.13) in this part of the linac, 3-gap cavities of length 5/2 would have a higher effective shunt impedance than 2-gap cavities. But at low , they do not leave enough room for the magnets. We can use inefficient 2-gap cavities for the lowest-energy section of the CCDTL because the accelerating gradient is low to match the longitudinal focusing strength at the RFQ exit.

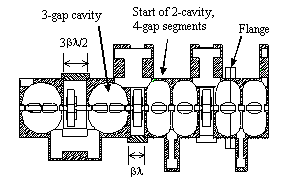
As the accelerating gradient increases, we start paying a power penalty in the 2-gap cavities. At the lowest that has enough room for EMQs in the length 3/2, we switch to the more efficient 3-gap CCDTL. Figure 2 shows the transition at 8.1 MeV. We use the term "segment" to refer to one or more contiguous accelerating cavities between two focusing magnets. The nominal length of this 3-gap cavity segment is 5/2. For structures in which the cavities share a common wall, the nominal length would equal the actual cavity length (including half the wall thickness). However, these APT segment contain only single 3-gap cavities. To support the vacuum loading, we use a somewhat thicker wall, so not all of the 3/2 space between cavities is available for EMQs. The same situation applies to the end cavities for all the different types of CCDTL and CCL segments.
By comparing the first two figures, it is evident
that some adjustment of the EMQ spacing is necessary to avoid
an abrupt change in spacing where the 3-gap cavity segments start.
The EMQ must fit inside the first 3/2 space between cavities.
To accommodate this requirement we gradually shift each EMQ slightly
upstream in successive spaces. Thus, the actual spacing between
EMQs is just under the nominal 4 and the magnetic focusing lattice
remains smooth across the transition. The focusing magnet in the
last 5/2 space is as far upstream as possible. In the next space,
we fill the available space with another 1-long cell on the upstream
side of the following cavity.
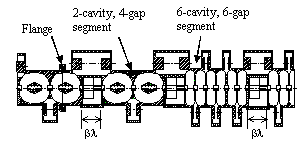
Figure 3 shows the next transition at about 20 MeV, where the structure changes to pairs of one-drift-tube CCDTL cavities. This transition includes the first of several increases in the bore radius. A compromise between shunt impedance considerations and the consequences of beam particles striking the accelerator influence the selection of the cavity bore radius. The bore radius affects the shunt impedance ZT2 mainly through the transit-time factor T. A smaller bore improves ZT2, but increases the likelihood of beam loss. On the other hand, relatively little damage or radioactivation of the structure occurs if low-energy particles strike the surface.
Beam-dynamics simulations [8] show that an initial
CCDTL bore radius of 1.0 cm is sufficient to capture the entire
RFQ output beam. No beam is lost even with the expected misalignment
of the EMQs. The RFQ beam edge is very sharp, essentially free
of any halo. The pole-tip inner radius of the EMQs at 6.7 MeV
is 1.4 cm. The magnets fit over stainless-steel bore tube, which
is brazed into the accelerating structure through a short bellows.
At 20 MeV, the bore radius increases to 1.25 cm. Two more increases
occur within the 2-cavity, 4-gap section of the linac. The next
step to a radius of 1.5 cm occurs at about 31 MeV, and then another
step to 1.75 cm occurs at 55 MeV. At each step in bore radius,
the structure efficiency decreases, but then it recovers as the
cell lengths increase in a section of fixed bore radius.
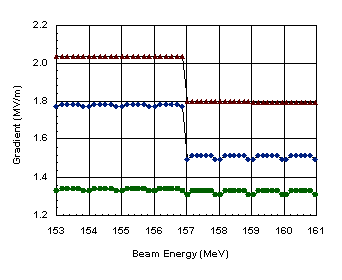
Figure 4 shows the transition to 6-cavity CCL segments, which occurs at about 100 MeV. The drift space between segments remains in length and the bore radius remains 1.75 cm through this transition. At 125 MeV, the bore radius increases to 2.0 cm. Starting at about 157 MeV, the segments become groups of seven cavities with a drift space of length /2. At this point we also make the last increase in the bore radius to 2.5 cm. This structure and the lattice period of 8 both continue all the way to 1.3 GeV. Figure 5 shows the last 7-gap segment of the linac.
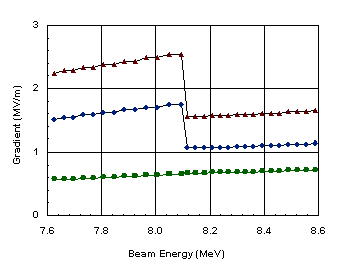
In a linac such as APT with its constant 8 focusing period after the RFQ, the transverse focusing strength per unit length remains constant through transitions in accelerator structure type. The key to maintaining a smooth average longitudinal focusing strength is an adjustment of the accelerating field E0 at each structure transition. In this regard, we distinguish between E0, the axial field gradient averaged over the active cavity length, and the "real-estate" gradient, which includes the transit-time factor as well as the packing fraction. We define the packing fraction as the ratio of active structure in a period to the period length. We present three examples of how E0 changes at transitions in the APT linac. Figure 6 plots the accelerating gradient for several segments of the APT linac on either side of the change in cavity type at 8.1 MeV (see Fig. 2). Each point represents a cell containing a single accelerating gap. There are two cells per cavity below the transition energy and three cells per cavity above it. The average axial field is constant within a cavity, so points appear in pairs of equal E0 below 8.1 MeV and in groups of three above the transition. In this case, the bore radius remained fixed at 1.0 cm, so the transit-time factor differs only slightly between cavity types. The main difference is the change in the packing fraction.

Figure 7 shows E0 and E0T for several segments on either side of the change in bore radius at about 31 MeV. The cavity type on both sides of the transition is the same, consisting of 2-cavity, 4-gap segments. Because the packing fraction does change, the real-estate gradient (not plotted) is just E0T reduced by the constant factor 0.75 through this energy range. The larger-bore cavities require a higher field level because of a ~5% reduction in the average transit-time factor. These changes in the field level occur within the same rf module. Unequal coupling-slot sizes on either side of a coupling cavity introduce the required step in the field level in adjacent accelerating cavities. We set the slot sizes during the low-power tuning of the structure before furnace brazing the copper assembly.
Figure 7 illustrates an important effect included in the new PARMILA code [] used to simulate the beam-dynamics performance of the CCDTL. The outer gaps in these 4-gap segments have a lower transit-time factor T than the inner gaps because the axial electric field penetrates into the connecting bore tubes. Inner gaps share one Dirichlet boundary between cavities, which improves T relative to the end gaps. The larger bore degrades T for both inner and outer gaps, but the degradation in the outer gaps is worse. Thus, above 31 MeV, there is a larger difference in E0T between the inner and outer gaps.
The third example includes a change
in the bore radius from 2.0 to 2.5 cm as well as an increase in
the packing fraction from 0.75 to 0.875. Figure 8 shows the transition
from 6-cell CCL segments to 7-cell CCL segments at 157 MeV. Again,
E0 is constant through a segment containing either
6 or 7 cavities. Transit-time factors for the end cells are noticeably
lower relative to the inner cells of a segment. This effect is
not as pronounced as in Fig. 7 because the cells are longer. The
particle velocity has increased from 0.25 to 0.51.
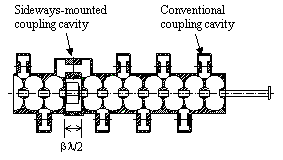
Successive accelerating gaps are n/2 apart, where n is an integer. Within the same CCDTL cavity n = 2, and for adjacent CCL cells n = 1. When successive gaps are in different cavities, the type of coupling cell between accelerating cavities depends upon whether n is even or odd. Figures 1 to 5 include examples of both schemes. Drift lengths noted in the figures are /2 shorter than the distance between the gap centers. The flexibility of two coupling-cavity orientations offers important advantages. First, it allows changes in the rf cavity type (for improving efficiency) without changing the focusing period. Second, it permits a large packing fraction throughout the major portion of a high-energy linac such as the APT.
Further explanation might be helpful. Coupling cells are nominally unexcited in a chain of cavities operating in the /2 structure mode. In conventional coupling cells, the axial electric field of the TM010 mode is parallel to the beam axis and the magnetic field has the same direction at both slots. This cavity remains unexcited in the /2 mode because the magnetic field of the two adjacent cavities drive it with equal and opposite strength. Thus, the conventional cavity orientation is appropriate for odd n where adjacent accelerating cavities have fields that differ in phase by 180 degrees. The sideways mounted cavity works for even n. Fields at the two slots are in opposite directions, so the cavity remains unexcited if the adjacent cavities are in phase. Side-coupled linacs have used conventional coupling cells for many years. We have successfully tested sideways-mounted coupling cavities on several CCDTL low-power models.
We have discussed design procedures
for high-current ion linacs that help to achieve smooth transverse
and longitudinal focusing throughout the accelerator. Examples
of rf structures from the 100-mA cw linac for APT served to illustrate
the design strategies. Beam-dynamics simulations discussed in
other papers at this conference show no growth in the transverse
emittance and only small growth in longitudinal emittance.
This work is supported by the US Department
of Energy.
[1] J. H. Billen, F. L. Krawczyk, R. L. Wood, and L. M. Young, "A New RF Structure for Intermediate-Velocity Particles," Proceedings of the 1994 International Linac Conference, Vol. 1, p. 341 (August 21-26, 1994).
[2] D. Schrage, L. Young, J. Browman, J. Merson, and A. Naranjo, "Conceptual Design of a 7-MeV RFQ Linac for the Accelerator Production of Tritium," Los Alamos National Laboratory report LA-UR-93-1790 (May, 1993).
[3] L. M. Young, "An 8-Meter-Long Coupled Cavity RFQ Linac," Proceedings of the 1994 International Linac Conference, Vol. 1, p. 341 (August 21-26, 1994).
[4] T. P. Wangler, J. H. Billen, A. J. Jason, R. E. Shafer, J. Staples, H. Takeda, and P. Tallerico, "High-Power Linac for a US Spallation Source," this conference.
[5] R. A. Jameson, "Report of the International Fusion Materials Irradiation Facility (IFMIF) Conceptual Design Activity (CDA) Accelerator Team Meeting," Los Alamos National Laboratory Report LA-UR-95-1701 (April 30, 1995).
[6] H. Takeda, J. H. Billen, S. Nath, J. E. Stovall, R. L. Wood, and L. M. Young, "A Compact High-Power Proton Linac for Radioisotope Production," Proceedings of the 1995 Particle Accelerator Conference, Vol. 2, p. 1140 (May 1-5, 1995).
[7] S. Nath, J. E. Stovall, H. Takeda, and L. M. Young, "Physics Design of APT Linac with Normal Conducting RF Cavities," this conference.
[8] S. Nath, J. E. Stovall, H. Takeda, and L. M. Young, "Front-End Physics Design of APT Linac," this conference.
[9] H. Takeda, L. M. Young, S. Nath, J. H. Billen, and J. E. Stovall, "Linac Design Algorithms with Symmetric Segments," this conference.
[10] J. E. Stovall, E. R. Gray, S. Nath, H. Takeda, L. M. Young and K. R. Crandall, "Alignment and Steering Scenarios for the APT Linac," this conference.
[11] R. L. Wood, F. E. Sigler, W. L. Clark, and F. A. Martinez, "Thermal/Structural Design and Fabrication Development of High Power CCDTL and CCL Structures," this conference.
[12] K. C. Dominic Chan, "Conceptual Design of a Superconducting High-Intensity Proton Linac," this conference.
[13] K. R. Crandall, "Ending RFQ Vane Tips with Quadrupole Symmetry," Proceedings of the 1994 International Linac Conference, Vol. 1, p. 227 (August 21-26, 1994).
[14] H. Takeda and J. E. Stovall, "Modified
PARMILA Code for New Accelerating Structures," Proceedings
of the 1995 Particle Accelerator Conference, Vol. 2, p. 2364 (May
1-5, 1995).