This paper summarizes our ongoing effort on the design of rf-extraction structures for the rf power source of a future TeV linear collider based on using the relativistic-klystron two-beam accelerator technology to drive Next Linear Collider structures (TBNLC). Several structure configurations involving different geometries and materials are examined using 2D and 3D computer code simulations. Three-cell detuned traveling wave structures and three-cell detuned choked -mode traveling wave structures are found to be the most attractive.

The two-beam-accelerator (TBA) concept has an inherent high efficiency for power conversion from drive beam to rf power. LBNL/LLNL has launched a study based on a Relativistic-Klystron Two-Beam-Accelerator (RKTBA) [1] to provide a rf power source for the Next Linear Collider (NLC). In this concept a single intense energy electron beam is used to power a number of rf output structures. A small fraction of the beam energy is extracted in each structure, and the beam is then reaccelerated before the next structure. The use of a single beam for many rf outputs can lead to increased efficiency and lower cost.

The main goal of this work is to provide a realistic design of rf-extraction structures using 3D numerical simulations. The rf-extraction structures should have surface electric field below the electrical breakdown voltage 70 MV/m, should have high efficiency with low BBU growth over 100 structures, and should be cost effective and compact. Each rf-extraction structure must produce 360 MW for the TBNLC parameters described in Table I.

Table 1. Power Source Requirements for TBNLC

rf frequency 11.424 GHz

rf current 1,150 A

repetition rate 120 Hz

peak power/structure 360 MW

distance between extraction structures 2 m

pulse length 300 ns

We perform full three-dimensional electromagnetic simulations of the complete cavity geometry, including output structures via full 3D self-consistent particle calculations and with the assumption of rigid beam. Most of the 3D calculations are performed using the 3D electromagnetic code MAFIA with the stiff beam approximations. An alternative 3D electromagnetic code ARGUS is used to cross-check the MAFIA results, while full particle simulations are used to cross check the stiff beam approximation results.

The considered geometries include multi-cell TWS, choked-mode multi-cell TWS, and structures employing pill-box cavities, reentrant cavities, tapered cavities, disk-loaded cavities, choke cavities, and Bragg Reflector or corrugated cavities. Here we present the two most promising designs we obtained.

The transverse beam dynamics of the multi-bunches are first examined against the dipole wakefield assuming one macro-particle per bunch. Then wakefield effects within a bunch are examined.

The 3-cell TWS have the following features; (1) They are inductively detuned, i.e. the phase velocity of the electric field of the structure is greater than the beam electron velocity, to enhance the longitudinal stability, (2) TWS is chosen to reduce the surface electric field, and (3) the smallest number 3 for TWS is chosen to minimize beam break-up (BBU).

Based on 2D calculations, earlier work of LBNL/LBNL lead to a conceptual design of the 3-cell inductively detuned traveling wave structure( ID-TWS ) shown in Fig.1.

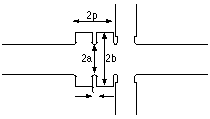
We carry out 3D particle simulations of the 3-cell ID-TWS for a train of 1000 Gaussian bunches of 600 A of DC current with 1150 A of rf component. A sinusoidal output power is obtained after the initial transient ramp-up phase. After the ramp-up phase the time-averaged power of 180 MW from an output waveguide, or 360 MW per structure is indeed obtained. The output power is calculated by evaluating Poynting vector over the cross-sectional area at each WR90 output waveguide exit. The 3D simulation also indicate that the detuning angle between the field and electron bunches is 60 degrees rather than 90 degrees found in the periodic 2D geometry with no output structures.

Beam transport over many structures is a crucial concept in a TBA. The betatron node scheme is an effective method for reducing BBU. By spacing the structures at betatron wavelengths of the focusing system, particles experience the least transverse kick. In reality there exists some mismatch of this betatron node scheme due to errors in the focusing systems, and nonuniformity in beam energy. The beam centroid can then be driven to oscillate with exponentially growing amplitudes. Here we wish to present the transverse beam dynamics in such realistic situations.

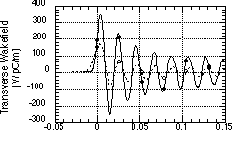
The transverse beam dynamics can be examined either in the real space utilizing the transverse wakefield, or in the frequency space utilizing the transverse impedance. The BBU of the 3-cell ID-TWS was studied earlier, in the frequency domain, using the OMICE code [2]. Here we present the BBU calculation in the real space via MBBU code [3]. Figure 2 shows the dipole wakefield of the 3-cell ID-TWS in the 2D approximated geometry. Shown are the transverse wakefields of a 11.4 GHz Gaussian bunch with s=3mm (solid) and s=6mm (dotted) where s is the standard deviation length of a Gaussian distribution. For clarity wakefields only up to about 6 bunch spacing are shown. The filled circles and open circles indicate the wakefields at centers of bunches. Higher wakefields are seen for the shorter bunches. Since a small increase in wakefield magnitude results in a cumulative BBU over many bunches and traveling many structures, the bunch length needs to be compromised with respect to BBU.

The MBBU code assumes each bunch as an object, ignoring interactions between particles within a bunch. First, for simplicity, we assume one macro particle per bunch and equal spacing between bunches. The transverse displacements, xj, of the j-th bunch with energy gj can be represented in the following BBU equation.

where z is the axial coordinate in cm, sb is the distance between bunches in cm, in cm-1 is the betatron wavenumber due to the focusing field, W is the transverse wake function in cm-3, I is the average current in z in kA, and Io=mc3/e =17.05 kA. Here

where is structure index, is the periodic length of structures, is one structure length, and BBU is tested over a device of 100 structures. The bunches experience a transverse kick while traversing the structures, and then translate down the beam pipe. The function G(z) reflects this alternating process. The numerical integration is required only in the structure region, while we utilize the transfer matrix in the drift region. We can further simply the BBU equation if << . In such cases we can approximate the transverse momentum kick during traversing the rf-extraction cavities as a delta-function kick;

.

We can then transform the equation into matrix multiplication. In Figs. 3-5 we present the BBU results using the MBBU code for the wakefield of the Gaussian bunch of s=3mm (solid line in Fig.2). For Figs. 3 and 4 only the wakefields at the bunch centers are considered in the BBU calculation. The initial beam displacements were assumed to be uniform with no transversal momentum for all cases. An average beam current of 600 A with 10 MeV beam energy, and betatron length of 2 m are considered.

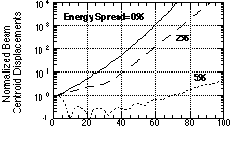
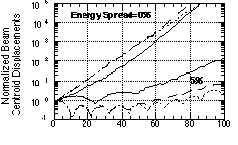
Fig. 3 summarizes the BBU in the 3-cell ID-TWS over 100 structures for various energy spread within a bunch. If the energy spread is larger than ± 5 %, due to the Landau damping, the BBU can be reduced to an acceptable level over 100 structures.

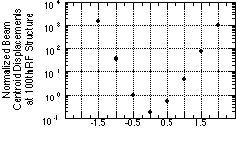
In Fig. 4, we show the transverse beam centroid displacements with respect to the mismatch in focusing field or the beam energy at the end of 100 structures, for the 3-cell ID-TWS with the betatron node scheme, assuming ±5% beam energy spread within each bunch. The 3-cell detuned TWS shows acceptable BBU with the betatron node scheme with respect to a ±1% error in energy flatness and field accuracy. For good beam transport it is expected that a 1% error in focusing field can be tolerated. The BBU in Figs. 3 and 4 show similar results as the previously published OMICE code results [2]. Detailed comparison of the two code results are being investigated.

Next we include the finite size of a bunch and the wakefield effect within a bunch. Imagine that each filled circle in Fig. 2 is stretched along the solid line over a finite length; 2s and 0.2s. We then divide each bunch by 11 slices uniformly over 2s and by 3 slices over 0.2s respectively. The BBU results are shown in Fig.5 over 100 structures with 0% and ±5% energy spread within each slice. Shown are results for one macro particle per bunch with zero length (solid), 3 slices over 0.2s bunch length (dashed) and 11 slices per bunch over 2s bunch length (dotted). Landau damping effect works more effectively with finite size bunches.

In order to transport a beam over many output structures one has to damp higher order modes (HOM), that lead to BBU and degrade the beam dynamics, while keeping the fundamental mode unaffected. Narrow structures on a pill-box cavity, or choked-mode cavity, with a beam pipe can trap the fundamental mode while higher order modes propagate into an absorber. Shintake [4] has proposed using a choke cavity structure for a high energy linac. Here we apply the concept to a 3-cell traveling wave choke structure for an rf-extraction structure. The choke structure shown in Fig. 6 is cylindrically symmetric except for the two output waveguides attached to the last cavity.

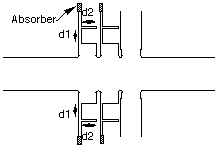
Table 2. Choked-mode TWS parameters

cavity height 12.43 mm

cavity width 8.75 mm

choked cavity width (d2) 6.45 mm

choked cavity height (d1) 6.45 mm

choked cavity gap 1.00 mm

The transverse wakefield is smaller with the choked-mode structure than without[5]. More importantly the HOMs should damp out in a choked-mode TWS even if they do not propagate out of the cavity structure. This reduction in wake fields represents a significant advantage for a choked-mode TWS.

We wish to thank Dr. A. Sessler for valuable discussions.

[1] Westenskow, G. et al., "Relativistic-Klystron Two-Beam Accelerator Studies at the RTA test facilities". in this proceeding; Proc. 1996 Int. Linac Conf., Geneva, (1996). Also see references therein.

[2] Houck, T.L. et al., "BBU Code Development for High- Power Microwave Generators," Proc. 16th Int'l LINAC Conf., Ottawa, Ontario, Canada, p. 495, (1992).

[3] Kim, J.-S. et al., "The Standing Wave FEL/TBA: Realistic Cavity Geometry and Energy Extraction", Proc. of Part. Acc. Conf., Vol. 4, 2593 (1993).

[4] Shintake, T., "The Choke Mode Cavity," Jpn. J. Appl. Phys. Lett, 31, pp. 1567-1570, (1992).

[5] Henestroza, E. et al., "Simulations and Cold Test of an Inductively Detuned RF Cavity for the Relativistic-Klystron Two-Beam Accelerator", in this proceeding;

* Supported by DOE SBIR grants DE-FG03-95ER81974 and DE-FG03-96ER82179 (1), by DOE contract W-7405-ENG-48 (2), and by DOE contract AC03-76SF00098 (3).

† bk consulting, 518 Bavarian Ct., Lafayette, CA 94549