In linear accelerators, misalignments of the machine
elements can cause considerable emittance growth due to wake fields,
dispersion and other effects. Hence, tight limits are imposed
on machine tolerances, design parameters and methods of machine
operation. In order to simulate the beam dynamics in linacs, the
tracking code L has been developed. Including both single- and
multi-bunch effects, the behaviour of the beam in the machine
can be simulated and adjustments on parameters of the machine
elements up to complete correction techniques and operation procedures
can be applied. Utilization of the program is facilitated by a
graphical user interface. In this paper we will give an overview
over the capabilities of this code and demonstrate its efficiency
at attacking the problems associated with large linear accelerators.
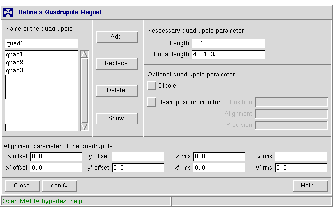
The tracking code L is embedded in the MAFIA software package. It is equipped with a graphical user interface (GUI), guiding the user through the simulation procedure. Figure 2 e.g. shows the dialogue for a quadrupole creation.
L is able to compute single and multibunch behaviour inside the accelarating structure. The single bunch case covers the development of the emittance, energy spread and the optical functions due to the influence of short range wake fields and structure misalignment.
The effects relevant for a multibunch simulation are:
The power of a new software is best demonstrated discussing an example. We will perform a tracking calculation in the first sector of the S-band linear collider (SBLC). This sector consists of 48 FODO cells. Each of them bears two accelerating structures of 180 cavities (total length 6m), one focusing and one defocusing quadropole magnet with an focal length of 4.3 meter. Another quadrupole with the double focal length is located at the beginning of the structure establishing a=0. Therefore the total length of sector 1 is 600 meter. In our example we will consider single bunch dynamics.
The principal simulation procedure is shown in Figure 1. We will follow this concept during this paper.
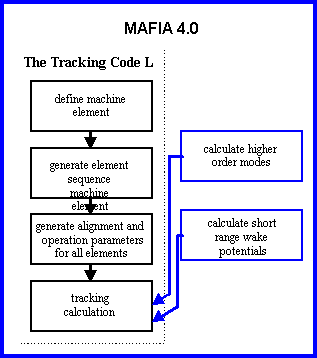
In the L-code no field problem on a discretised space is solved, but a sequence of transfer matrices belonging to the elements appearing inside a linear accelerator is defined[1]. Implemented elements are:
To each element a beam position monitor and a dipole magnet can be added. This feature is important for the application of correction techniques.
The following insufficienies can be attached to the elements:
Since no drift spaces appear in our example, we will start our input with the quadrupoles( Figure 2). The parameters required are the physical length and the focal length in meter. Finishing our input we add the new quadrupole to the list of existing quadrupoles.
At every time it is possible to display the parameters
of previous structure elements using the show button, change parameters
with the replace button or remove an unused element by pressing
the delete button.
We will continue in our problem description by defining the accelerating structures. The geometrical dimensions were already mentioned in the introduction. Furthermore the qualityfactor (Q=13500), the frequency (f=2.998 GHz), the loss parameter (k0 =1.11 1014 V/As) have to be defined. Depending on whether single or multibunch dynamics are to be calculated, the short or the long range wakefields respectively have the main influence on the result of the calculation. We will restrict ourselves to the investigation of the single bunch behaviour. Consequently we need the short range wake information[4].
The bunchlength in the SBLC collider is s=300mm. The wakefield calculation takes place in the MAFIA-T2-module. The longitudinal wakepotential in a range of 13s from the bunch head is needed. L is able to consider monopole, dipole and quadrupole wakes. The transverse wake potential is calculated by means of the Panofsky-Wenzel-theorem.
In a multibunch calculation the frequencies of the
modes in the several passbands must be supplied.
After having defined every single element of the machine is, we continue with glueing the primitves together to a more complex structure, a so called module. In our example we take 2 accelerating structures and as well a focusing as a defocusing quadrupole and put them together in a FODO-cell.
It is possible to combine previously build modules with other elements, each of them with an arbitrary number of repetitions. In this facil manner we can construct sector 1 of the SBLC from the 193 elements within one minute.
After the modules are expanded into a structure, the misalignments to elements and classes are set by means of a random generator. Furthermore L offers the application of the slow ATL-ground motion to the final lattice.
Even in this state every single setting is accessible
via the graphical user interface.
Every particle inside the bunch (1.1 1010 particles in case of the SBLC) has different initial offsets (x, y), slopes (x', y'), energies (W), and longitudinal positions (s). In order to model the bunch with a moderate numerical effort, it is divided into several slices, distributed equidistantly over its range. Assuming no uncorrelated energy spread each particle inside one slice has the same energy. L offers the feature to include the uncorrelated energy spread by defining subslices inside one slice.
To analyze the multibunch dynamics it is often sufficient
to assume the single bunches inside the bunchtrain to be pointlike
charges. Nevertheless it is possible to divide every bunch into
slices and to examine the combined single and multibunch effects.
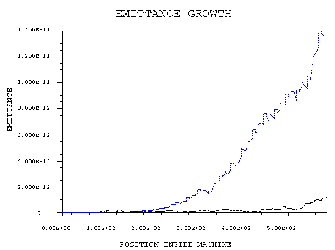
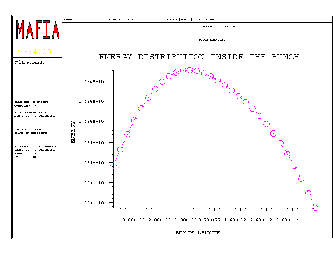
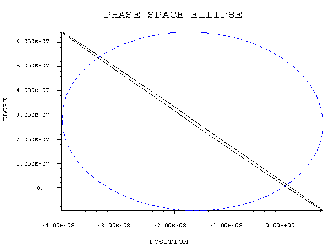
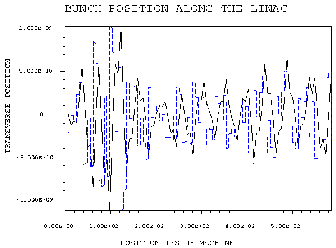
The next step is starting the calculation. After 2 minutes calculation time the results of the first shot through the machine are available, such as the emittance(see Figure 3), the energy distribution (Figure 4), the phase space ellipse (Figure 5) or the trajectory of the bunch (Figure 6).
The L-code calculates the beam dynamics in both transverse directions in one run. Furthermore it provides the possibility to switch single effects (e. g. all longitudinal wake fields or only dipole wakes) on or off right before the tracking calculation commences.
The code is intended not only for static analysis
of emittance growth in a linac but rather for the simulation of
complete linac operation. Therefore several features have been
added allowing to simulate both perturbing effects occurring at
machine operation and the application of advanced trajectory and
emittance correction techniques. The effects perturbing machine
operation include for instance random fluctuations of the bunch
charge, jitter of the bunch positions or slow displacement of
machine elements due to inelastic ground motion [3]. On the other
hand, machine elements can be equipped with beam position monitors
simulating the measurement of the transverse beam offset relative
to the elements and with dipole magnets deflecting the beam. Thus
the user can create his own correction procedure in the MAFIA
command language, reading the beam positions or emittance profile
obtained in the tracking calculation and then correct the beam
emittance by adjusting any machine parameter (element displacements,
deflection angles of dipole magnets ...) This feature has been
applied successfully to a variety of correction techniques like
Dispersion-Free and Wake-Free orbit correction, trajectory bumps
and others.
The tracking code L is a powerful tool to investigate both, the single and the multibunch behaviour inside a linear accelerator. Beyond that it is able to simulate the effects of different correction schemes. The graphical user interface will guide you securely through this matter.
[1] M. Drevlak,"On the Preservation of Single- and Multi-Bunch Emittance in Linear Accelerators", DESY 95-225, (1995)
[2]"International Linear Collider Technical Review Report 1995"SLAC-R-95-471, (1995)
[3]B. A. Balakov et al.: "Investigation of Seismic Vibrations and Relative Displacements of Linear Collider VLEPP Elements", Proc. 1991 IEEE Part. Acc. Conf., San Fransico, USA, pp3273,1991
[4]T. Weiland, "On the Numerical Solution of
Maxwell's Equations and Applications in the Field of Accelerator
Physics", Particle Accelerators, 1985, Vol. 17, p 227-242