The low-level RF (LLRF) control system for the Accelerator Production of Tritium (APT) will perform various functions. Foremost is the feedback control of the accelerating fields within the cavity in order to maintain field stability within ±1% amplitude and 1° phase. The feedback control system requires a phase-stable RF reference subsystem signal to correctly phase each cavity. Also, instead of a single klystron RF source for individual accelerating cavities, multiple klystrons will drive a string of resonantly coupled cavities, based on input from a single LLRF feedback control system. To achieve maximum source efficiency, we will be employing single fast feedback controls around individual klystrons such that the gain and phase characteristics of each will be "identical." In addition, the resonance condition of the cavities is monitored and maintained. To quickly respond to RF shutdowns, and hence rapid accelerating cavity cool-down, due to RF fault conditions, drive frequency agility in the main feedback control subsystem will also be incorporated. Top level block diagrams will be presented and described as they will first be developed and demonstrated on the Low Energy Demonstrator Accelerator (LEDA).

Resonance control of each accelerator cavity is required in order to control the shift of the cavity's resonant frequency due to RF heating, beam loading, ... During normal operation of room temperature copper structures, resonance control is performed by providing a proper drive signal to structure cooling water valves to optimize match. In the superconducting case, a servo loop will be used to mechanically change the cavity's shape in response to resonant frequency shifts.

Because large amounts of cooling water will be running through the room temperature accelerating structures to accommodate RF heating, a fast shutdown of the RF will cause the cavity to cool down dramatically and cause a large shift in resonant frequency. Rather than rely on the cooling water system to bring the cavity back on resonance, we intend to employ a frequency agile system which will drive the klystron at the cavity's resonant frequency and slowly bring that drive frequency in to the nominal beam-required resonant frequency. In this manner we can quickly bring a cavity back on to resonance. This frequency agile function, based on direct digital synthesis, will be utilized only when the cavity is far from nominal resonance, not during normal operation.

For the room temperature linac, multiple klystrons will be driven by a single LLRF control system as shown in Figure 1.

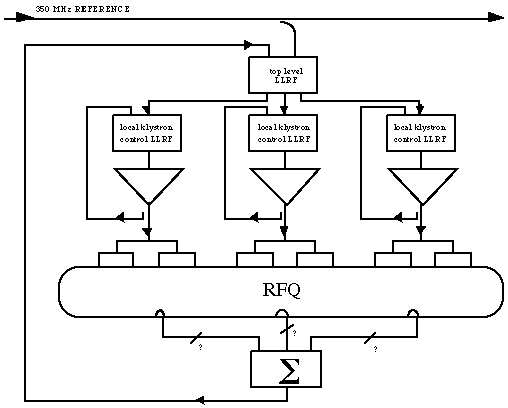
There is concern that by driving a group of klystrons, the overall LLRF control system will be attempting to compensate all of the klystrons for errors introduced by the "worst" one. Therefore in order to achieve maximum source efficiency, we intend to measure the amplitude and phase across each klystron and maintain a predetermined transfer function by applying local feedback control. This is used to linearize the multiple klystrons driving the single accelerator cavity and to negate phase drifts in those klystrons. Since power supply ripple typically occurs at line harmonics (low frequency), and the field control compensator has high low-frequency gain, we do not need to concern ourselves with the power supply ripple in this amplifier regulation loop. It will be rejected with the field control compensator.

The cavity field control functionality is divided into three separate compensators working in parallel. Each of these compensators has a frequency range over which it is most effective.

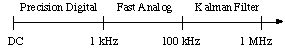
The Precision Digital compensator provides extremely accurate DC and low-frequency measurements by employing quadrature sampling and digital signal processing (DSP) techniques. Its bandwidth is limited to about 1 kHz by the digital throughput of the ADCs and DSPs. The Fast Analog compensator is implemented in high-bandwidth RF and analog circuitry to maximize the closed-loop bandwidth (limited to approximately 100 kHz by the group delay through the other components of the RF system. Transmission delay of up to 700 ns precludes feedback compensation for more than a couple hundred kilohertz). This type of fast analog electronics is susceptible to DC offsets and drifts and will have its low frequency gain reduced for those frequencies where the Precision Digital compensator is most effective. In order to extend the control bandwidth of the system, we intend to add-on an optimal state-variable Kalman Filter. The Kalman Filter uses statistical processing (and perhaps other complicated digital algorithms) to predict and correct the high-frequency errors. The Kalman filter will require a beam current signal, and possibly a cathode voltage, in addition to the RF field and drive signals, to perform its statistical processing and correction. The Precision Digital and Fast Analog compensators will be designed to allow independent or joint operation, while the Kalman Filter will be an add-on to improve performance.

The cavity field control system is based on the I/Q control functionality originally developed for the Ground Test Accelerator. It will consist of a four module VXIbus set: a Clock Module, a RF module, and a DSP module, and a Resonance Module. All RF and IF signals will be transmitted between modules using front-panel coaxial connectors. All of the baseband and digital signals will be transmitted over the VXIbus backplane. The Clock Module receives a 10 MHz reference and produces LO (650 MHz and 300 MHz), IF (50 MHz), and ADC (40 MHz) frequencies needed for downconversion and I/Q sampling. The RF module contains all of the RF electronics for the entire control system. The DSP Module is primarily a digital module that performs two functions: the high-precision I/Q detection and control, and the modern control algorithms that extend the control bandwidth. The Resonance Module performs three basic functions: provides a resonance control signal to the water temperature controller that maintains resonance; provides an open-loop I/Q control signal that can adjust the LLRF output amplitude, phase, and frequency; and performs the calculation for amplitude and phase equalization needed to balance the three klystrons. An overall block diagram of the LLRF control system is given in figure 2.

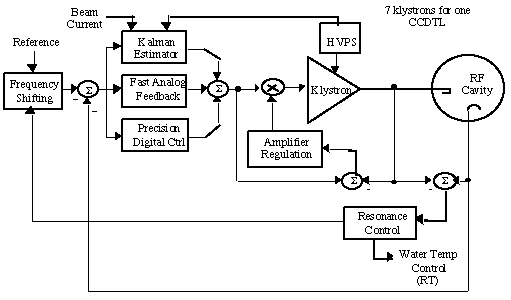
Samples of the RF field inside the accelerating structure, the drive from the klystrons, and reflected power signals are all fed back to the LLRF control system located near the multiple klystrons it drives. (This "supermodule"/multiple klystron concept is described in [1]). The field, drive, and reflected RF signals are mixed with a local oscillator locked to the master oscillator RF reference in order to produce IF signals (50 MHz) for quadrature and digital sampling. In addition the field IF signals are downconverted a second time to produce baseband I/Q signals. These baseband signals are processed in the following order: (1) Error correction, phase rotation, and scaling of the field I/Q signals is accomplished by a 2-by-2 multiplier. (2) Error signals are provided by subtracting the measured field I/Q signals from the I/Q setpoints. (3) The error signals are applied to the baseband control filter. (4) The baseband I/Q control signals from the DSP module are added to the filter-compensated signals. (5) A 4:2 multiplexer selects either these closed-loop control signals or the open-loop drive signals generated by the Resonance Module as the signals that define the LLRF output. (6) The baseband control signals are split three ways and processed by three 2-by-2 multipliers that provide the phase and amplitude equalization for the three klystrons driving the single accelerator cavity (RFQ). (7) The three resulting baseband I/Q signals are double-upconverted back to the RF frequency.

The precision digital I/Q detection and control is accomplished as follows. The 50 MHz Field IF signal is I/Q sampled at 40 MSPS to provide very accurate I/Q data (no DC offsets, no amplitude imbalance) and data are processed in a pre-processor that performs very high speed digital filtering and decimation required to reduce the data rates down to those appropriate for a general purpose DSP. For a digital loop bandwidth of 1 kHz, data are processed around 10 kSPS. The filtering rate reduction from 20 MSPS (for 40 MHz I/Q sampling) to 10 kSPS for the I/Q data provides the compensation (PI, cross-coupling, etc.) needed to produce the digital I/Q control outputs. Analog signals are created from these digital control signals in DACs. The general purpose DSP also provides the I/Q setpoints that are used both within its own algorithms and by the RF module for baseband analog processing. Therefore, I/Q setpoints are generated by the general purpose DSP, converted to analog signals in DACs, and transmitted to the RF module. The modern control algorithms are accomplished in parallel to this process in the following manner. The same sampled I/Q data are processed in a separate processor that provides the +/-1 multiplication, and possibly some filtering, but does not reduce the data rates significantly. For this reason the general purpose DSP cannot be used. In order to provide 1 MHz of control bandwidth, data rates around 10 MSPS have to be maintained. Consequently, the Kalman Filter DSP has to be implemented as discrete high speed digital components capable of maintaining the 10 MSPS rates. The Kalman Filter DSP uses the field I/Q data along with sampled beam current data to perform the modern control algorithms that result in digital I/Q control signals that are converted to analog signals in DACs. The two analog control signals are combined and transmitted to the RF module for I/Q modulation. We are considering performing the extra function digitally and use a single DAC to convert the combined signal to analog.

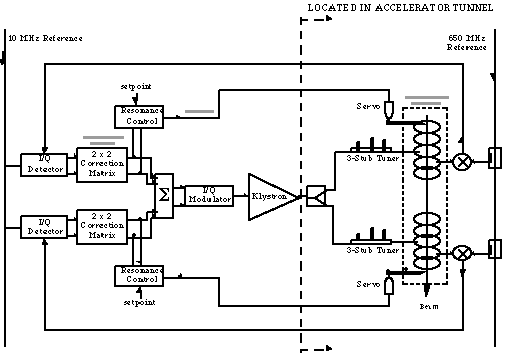
Preliminary LLRF control system design for the superconducting portion of the linac has taken place. The largest difference between the room temperature (RT) and superconducting (SC) portions of the linac from a control system standpoint, is that we provide a drive signal to multiple klystrons for RT, but for SC, we drive a single klystron which puts power into multiple accelerating cavities. For the medium beta section of the superconducting portion of the linac, we anticipate driving three linked cavities within a single cryomodule with a single LLRF control system and one klystron split three ways. (The high beta section will only have two cavities per klystron). Control of the fields in these linked cavities is based on an arithmetic average of the field probes within each of the cavities fed back to the LLRF system. The concern with this system is that should one cavity become dramatically detuned, or loaded relative to its companions, we will be compensating the drive to all in order to really only take care of problems in the one. Hence, we also intend to have individual cavity control to compensate for any individual cavity errors. Individual cavity control will be comprised of a mechanical servo-driven tuner for resonant frequency compensation. The overall LLRF feedback loop will be identical to that of the room temperature structure. Combining the overall loop with individual cavity control should provide us with the ability to control the fields in the cavity well within the required ±1°, 1% for the linked cavities, or ±3°, 5% individually. See figure 3 for a conceptual block diagram of the superconducting system.

The required functions and their implementations for the LEDA/APT low-level RF control system have been described. Presently we are modeling the various components, and schematics and breadboarding are on-going.