The main laws that govern gentle bunching of Space Charge-Dominated (SCD) beam are considered. It is shown that SCD-beam bunching depends on two main parameters: the first one determines the bunching quality, another one is measure for bunching process duration. The changes in bunching process depending on this parameters and on low of RF-field amplitude increase are described. The optimal conditions of SCD-beam bunching are discussed. The computer codes ZHALO generated for bunching beam characteristic visual representation are described.

An adiabatic bunching section must be presented at a high-current ion linac for beam loss prevention. The problem is to choose an optimal length of the section as well as optimal values for synchronous phase and accelerating field amplitude. In order to clear up the main regularities of the bunching process the simplest model was used by analogy with the previous case. In the context of this model the beam without transverse motion and with fixed transverse size is moving inside a channel with bore radius R. Synchronous phase is equal -90 degrees and the beam is bunching without acceleration. During bunching process the uniform beam gets a longitudinal charge density modulation. The distribution of potential can be obtained in the form of an expansion into a series by solving a Poisson equation for the beam with periodical charge density modulation and uniform density in any transverse crossection

where w = 2p/L, L is length of modulation period, function C(x,y) is defined via Bessel cylindrical function I and K

r_k(r) are coefficients in the Fourier expansion into a series for periodical function

The equation for Coulomb field intensity has a form

where q_k is harmonic coefficient in the expansion of . Setting we obtain for the field at the axis of beam

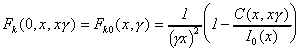
In this case

and F_k0(x,g) decreases exponentially with x growth. The general form of F_k0(x,g)/D₀ for g values from 0.1 up to 1 with 0.1 as a step is indicated on Fig.1. We will be called these functions the harmonic factors. It can be seen that any harmonic factor is lay between 0 and 1.

Using unitless variables

and the harmonic factors for Coulomb field defined above the equation for bunching process analysis can be obtained

where function H(t) describes the general rule of the first harmonic of accelerating field growth up to maximum value E_m.

The general view of the above equation shows that in the context of given R_b/L and R_b/R_a the bunching process depends on the single parameter

By this means the task is reduced to the optimal form of function H(t) which allows maximal a for the bunching process without beam losses.

The introduced Coulomb parameter a differs from commonly accepted one. It is evident to factor out the term 1/(wR_b/L) from the equation for bunching process analysis and join it to a. The new approach underlines that the Coulomb field determines by parameter a but relations R_b/L and R_b/R_a shows only geometrical similarity. The Coulomb parameter decreased with an energy growth whereas harmonic factors are increasing. But their growth is limited because the values are between 0 and 1.

The image-based simulation code package ZHALO was generated for investigating space charge-dominated beam bunching. In the context of the bunching model considered here, the Poisson equation is solved with initial conditions that correspond to a mono-energy beam with a uniform phase distribution across the full RF period. The function H(t) was taken in the form

where the coordinate t_m and beginning level of field E₀/E_m are given.

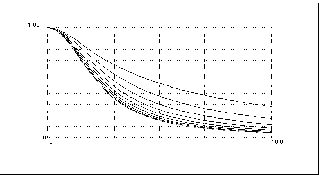
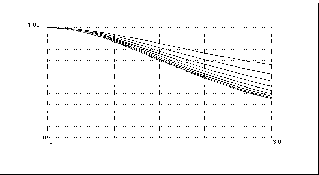
The following "images" are used as subjects of inquiry: (a) a Coulomb field distribution (on the background of external field sinusoid), (b) the beam charge distribution, (c) a distribution of particle kinetic energies on the background of Coulomb field intensity distribution U_k(z) = U(0) - U(z), (d) the beam phase portrait on the background of the external field separatrix, (e) a phase length of an "equivalent" bunch with uniform density along z and the same rms-size, (f) a Coulomb field harmonic spectrum (plots of the first five harmonics).

To determinate R_a/L and R_b/R_a a beam with parameters typical for a high-current CW linac was chosen: f = 350 MHz, R_a = 3 mm, beam energy W = 0.1 MeV, R_b/R_a = 0.5. (In the context of the chosen parameters, the value (a = 1 corresponds to current 0.4 A if E_m = 1 MV/m). When the investigation was made with a growing RF field, E_o/E_m = 0.2 was taken.

A visual inspection of a SCD-beam bunching with increasing of a parameter step by step gives us a general view of the process depending on a.

It is evident that particles with initial positions near the bunching center achieve this center at an earlier instant of time and form a Coulomb potential barrier for other particles. During the first quarter of the phase oscillation period this barrier is increasing and each next particle meets a bigger opposition then the previous one. It means that during the first quarter of the phase oscillation period a high-density core is formed inside the bunch.

Starting from some value of a the energy needed for a particle to overcome the Coulomb barrier may be comparable with the kinetic energy that the RF field has given to this particle. The typical points of inflection appear in the phase portrait. For this and for all bigger a-values the beam can be called a SCD-beam. On further a growth particle energy loss becomes larger as the center is approached. In its turn, the phase oscillation amplitude can be increased owing to added momentum which a particle has assumed in escaping from the core. As it will be shown below at this stage the fraction of particles which escape the phase period rises sharply. We call such particles "lost" ones.

The final stage of a growth leads to the situation where particles are completely decelerated by the core Coulomb field and the particle cannot pass through the core.

Nevertheless, as also indicated below beam bunching can take place in this case as well. To do this, it is necessary to "match" the rate of Coulomb barrier growth with the growth of particle kinetic energy. The "matching" can be made by the choice of E_o/E_m and t_m values.

A comparison between beam bunching in a channel where RF amplitude is constant (case A) and in a channel where RF amplitude is build-up (case B) shows that in the first case: (a) deformations of phase portrait start from a = 0.15, (b) the kinetic energy becomes comparable with the potential energy for a near to 0.25, (c) for a > 0.5 lost particle fraction rises sharply.

It is evident that there are two sources for particle losses caused by longitudinal motion. The first one is vertical narrowing of the stable oscillation zone. As a result of this factor boundary particles go out from this zone. When the RF amplitude is constant this effect is present also in the case of small a although the proportion of lost particles is small. The second loss source is amplification of the longitudinal oscillation for particles which pass the core in the stage when the core density is compacting. By analogy this effect can be named "halo formation". With a increasing halo oscillations are amplified. Starting from some value of a (in the case A a > 0.5) swing of the halo particle oscillation exceeds 2p.

Because of a small external RF field in the beginning of the channel with RF amplitude build-up (case B), Coulomb effects become detectable for a = 0.07.

Visual analysis shows that in the case B the essential influence of the core starts from a smaller kinetic energy of particles than in case A. In case B the total core charge is smaller. For the same a the added momentum from the core is small and it can not raise the amplitude of particle oscillations by a large margin. Although the Coulomb potential energy exceeds the particle kinetic energies, the bunching process takes place practically without losses up to a = 1.2 (for E_o/E_m = 0.2 and t_m = 1). It means that the limit current is doubled as compared to case A. The increasing of t_m up to 1.5 increases the a limit up to 1.4 but no more. Particles can not pass the core but the attraction momentum does not let them escape from the stability zone of bunching.

The comparison between constant and build-up RF field allows the statement that in Case B the beam phase rms length is essentially smaller. This statement is valid for zero current too.

A second trend has emerged from observation of the Coulomb field harmonic spectrum for a "frozen" beam. With increase in a the first harmonic of the Coulomb field far exceeds the other harmonics. Its amplitude approximates that of the external field. It may be concluded that the SCD-beam automatically makes Coulomb field distribution similar to external field distribution. Such a high-current effect can be considered as a beam "auto-matching" with a channel. Along with this for small a the higher harmonics are comparable with the first one and local resonance effects can be caused in the beam transverse motion.

Only motion along an accelerator axis was considered in the above investigations. A charge distribution also was generated by axis particles. In practical situations particle transverse oscillations take place. As can be seen from the equations for E_coul(r,z) and for E_ext(r,z) Coulomb field intensity is decreasing and external field intensity is increasing with the growth of r. It means that a particle during transverse oscillations experience a larger bunching forces as compared to axis particle.

Previous analysis is based on particles which are moving along longitudinal axis. The charge distribution is generated also by axis particles. In reality particle execute transverse motion. With regarding to increase of r Coulomb field intensity E_col(r,z) is decreasing but RF field intensity E_ext(r,z) is increasing. Bunching forces are larger for peripheral particles then for axis particles.

The corrections in the considered effects must be applied when longitudinal oscillation frequency depends on radius. It is not so easy to predict final result. On the one hand the Coulomb effects are decreasing because the relation between Coulomb and bunching fields is changed in favor of bunching one. On the other hand transverse non-uniformity leads to: (a) transverse velocity increasing for peripheral particles, (b) core density increasing due to (a), (c) core counteraction increasing for particles near axis.

Model for bunching process used in ZHALO.THEORY does not take into account particle transverse motion. But it can be considered the transverse motion of "radial layers" with the same and constant radius for all particle inside layer. Such model can not give the quantity description of transverse motion but can quality estimate longitudinal oscillation effects owing transverse non-uniformity.

Investigations with the use of ZHALO.THEORY show that all physical relations and effects brought out for particles near axis are valid in general case too. There is small quantitative difference between results in both cases. For the same a loosed particle number is larger in the "layer case" then in the "axis case". The last fact indicates that the effects from faster charge accumulation inside core by peripheral particles are stronger then effects from average phasing force increasing relative to Coulomb one.

[1] B.I.Bondarev, A.P.Durkin, A.Jameson "Space Charge-Dominated Beam Bunching", Report on Second International Conference on Accelerator-Driven Technologies and Applications (Kalmar, Sweden, June 1996).

[2] B.I.Bondarev, A.P.Durkin, "Study of Space Charge-Dominated Beam Bunching". Contract 1083P0015-35 between LANL and MRTI, Moscow 1995.