A bunched beam from an accelerator can excite and power an rf cavity which then drives either a deflecting or focusing (including nonlinear focusing) rf cavity with an amplitude related to beam current. Rf power, generated when a bunched beam loses energy to an rf field when traversing an electric field that opposes the particle's motion, is used to drive a separate (or the same) cavity to either focus or deflect the beam. The deflected beam can be stopped by an aperture or directed to a different area of a target depending on beam current. The beam-generated rf power can drive a radio-frequency quadrupole that can change the focusing properties of a beam channel as a function of beam current (space-charge-force compensation or modifying the beam distribution on a target). An rf deflector can offset a beam to a downstream sextupole, effectively producing a position-dependent quadrupole field. The combination of rf deflector plus sextupole will produce a beam current dependent quadrupole-focusing force. A static quadrupole magnet plus another rf deflector can place the beam back on the optic axis. This paper describes the concept, derives the appropriate equations for system analysis, and gives examples. A variation on this theme is to use the wake field generated in an rf cavity to cause growth in the beam emittance. The beam current would then be apertured by emittance defining slits.
Figure 1 shows the concept in a system designed to
aperture a high current beam. The RF generator and deflector are
conceptually shown as two units. The beam deflection angle is
proportional to the beam current. This deflection becomes a displacement
at the beam collimator. Permanent magnet non-linear focusing magnets
can enhance the operation of the RF deflector.
In this section, a differential equation describing
the rf field generated in a cavity excited by a bunched beam is
derived and solved. This differential equation depends on the
energy deposited in the cavity by the beam and the energy lost
in the cavity due to resistive wall losses. We consider a TM010
mode single-cell cavity (DTL type) where the electric field is
along the beam direction and is concentrated on the axis of the
cavity between the drift tube noses.
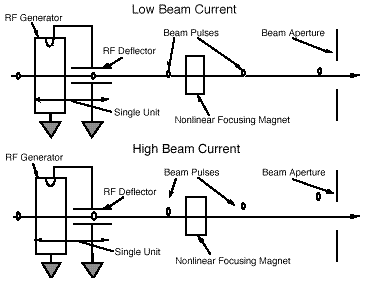
The bunched beam from the accelerator drives a cavity
that produces rf power which then drives a beam deflecting cavity.
The deflecting cavity could be followed by nonlinear magnets and
then phase-space defining apertures to remove the deflected beam.
Work done against the rf electric field by particles
traversing the gap adds energy to the rf field. This gain in the
field energy, ![]() , due to one particle is
, due to one particle is
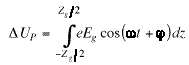 (1) where
(1) where
![]() (2)
(2)
e is the charge on an
electron, Zg
is the gap length, Eg
is the gap voltage, w
is 2p times
the rf frequency, b
is the velocity of the particle with respect to the velocity of
light, l
is the free space rf wavelength, v is the particle's velocity,
t is time, and j
is the rf phase when a particle enters the gap. Assuming that
the change in particle energy in crossing the gap is small compared
to the particle's kinetic energy and treating v as a constant,
Eq. (1) is integrated to obtain
![]() (3)
(3)
where, Eo
is an average field strength defined by
![]() , (4)
, (4)
and T is a transit time factor. The transit
time factor is defined as
![]() (5)
(5)
Equation (3) gives the energy gain in the rf electric
field due to one particle crossing the rf-gap.
The individual charges in a beam bunch enter the
rf-cavity at different phases j.
The phase distribution of the particles is described by the function
r(j).
The total charge per beam bunch is
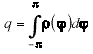 (6)
(6)
Let,
![]()
be the energy deposited in the cavity by a complete
beam bunch, and use Eq. (3) to obtain
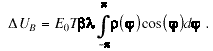 (7)
(7)
The integral in Eq. (7) can be defined in terms of
a dimensionless charge-distribution form factor as
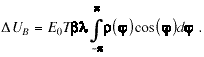 (8)
(8)
The value of F is less than 1 (it is equal
to 1 for a d
function distribution). This form factor is rather insensitive
to beam bunch length. For example, assume that r(j)
is described by the rectangular distribution
![]() , (9)
, (9)
where jo
is the phase extent of the distribution. Then,
![]() . (10)
. (10)
When jo
= 0, F = 1, and when jo
= p/2 (severe
debunching), F = 0.64. Equations (24) and (25) (derived
below) show that the maximum-generated electric field scales as
F. We see that the rf-electric field is somewhat insensitive
to significant beam debunching. Let UT
equal the total rf field energy in the cavity. The rf electric
field will scale as the square root of UT.
Combining Eqs. (7) and (8) and defining the constant k1
as
![]() (11) gives
(11) gives
![]() . (12)
. (12)
The constant k1
depends on the electric field distribution in the cavity and is
a function of the cavity geometry. We will later assume a model
for the electric field distribution that will permit a rough calculation
of k1.
Equation (12) gives the rf field energy gain
due to one beam bunch crossing the rf-cavity gap against the rf
electric field. There are power losses in the cavity due to the
finite resistance of the cavity walls. This power loss can be
determined from the Q of the cavity defined as
![]() (13)
(13)
where WL
is the average rf power loss per unit time. The rf energy loss
in one rf cycle (time t
= 2p/w)
is then
![]() (14)
(14)
The change in total rf power per time is
![]()
Using Eqs. (12), and (13) gives
![]() (15)
(15)
Equation (15) is easier to solve if Eo
[from Eq. (11)] is substituted for UT.
Equation (15) becomes
![]() (16)
(16)
Assuming that the rf power is zero when t
= 0, Eq. (16) can be integrated to give
![]() . (17)
. (17)
The charge per beam bunch, q, can be calculated
from the instantaneous average beam current, I, and is
![]() . (18)
. (18)
Substituting Eq. (18) into (17) gives
![]() . (19) where
. (19) where
![]() . (20)
. (20)
A crude estimate of k1
can be obtained by assuming that most of the rf electric field
is concentrated between the drift-tube noses and is a constant.
The maximum stored energy in the electric field can be calculated
and related to UT
to give k1.
The value of UT
calculated from the electric field is
![]() . (21)
. (21)
Solving this equation for Eg
and using Eq. (4) gives
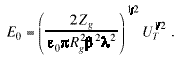 (22)
(22)
Comparing Eqs. (11) and (22) gives
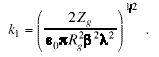 . (23)
. (23)
Combining Eqs. (4), (11), (13), (20) and (23) give
![]() (24)
(24)
![]() (25)
(25)
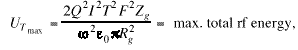 (26)
(26)
and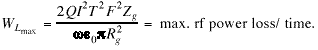 (27)
(27)
We calculate ![]() and
and ![]() using Eqs. (25) and (27) for a 100 mA
beam at 800 MeV. Assume a 10% beam duty factor, then I = 1.0 mA.
We let w/2p
= 200 MHz, Q=1000, j
= 1 deg, Z= 1.0 cm, and R= 1.0 cm (eo
= 10-9/36p).
Equations (25) and (27) give
using Eqs. (25) and (27) for a 100 mA
beam at 800 MeV. Assume a 10% beam duty factor, then I = 1.0 mA.
We let w/2p
= 200 MHz, Q=1000, j
= 1 deg, Z= 1.0 cm, and R= 1.0 cm (eo
= 10-9/36p).
Equations (25) and (27) give ![]() = 5.7x105
V/m (rf-gap voltage) and
= 5.7x105
V/m (rf-gap voltage) and ![]() = 5.7 watts
(maximum power extracted from the beam). We
calculate the beam deflection due to a transverse rf-electric
field. From,
= 5.7 watts
(maximum power extracted from the beam). We
calculate the beam deflection due to a transverse rf-electric
field. From,
![]() , (28)
, (28)
we obtain
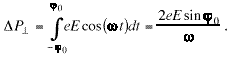 . (29)
. (29)
The deflection angle
![]() . (30)
. (30)
For E = 0.57 MV/m, fo = p/2 (complete rf half cycle), 5 rf deflection cavities (each of length bl/2 = 0.68 m), and an 800 MeV beam, we find that X' = 10-3 radians. This will produce a deflection of 1 cm in 10 meters. Given this same geometry, a 10 mA beam will have a deflection angle of 10-2 radians and will be deflected 10 cm. There are issues to be addressed if this system is to be used for limiting beam current for personnel safety. These include: sensitivity of the rf cavities to detuning, possible long term degradation in cavity Q due to oxidation of cavity surfaces, determining the envelope of off-nominal linac operational parameters that will cause the beam to sufficiently debunch so that the rf deflection system will no longer work, and rf cavity conditioning.
I would like to thank Paul Tallerico for several useful and interesting discussions.
*Work supported by the U.S. Department of Energy