The issue involved in the simultaneous matching of H+ and H- beams between an RFQ and DTL lies in the fact that both beams experience the same electric-field forces at a given position in the RFQ. Hence, the two beams are focused to the same correlation. However, matching to a DTL requires correlation of the opposite sign. The Brown-Servranckx [1] quarter-wave () matching transformer system, which requires four quadrupoles, provides a method to simultaneously match and beams between an RFQ and a DTL. The method requires the use of a special RFQ section to obtain the Twiss parameter conditions and at the exit of the RFQ [2]. This matching between the RFQ and DTL is described below.

Figure 1 shows the two-quadrupole- matching transformer with an additional quadrupole placed at each end to produce the appropriate Twiss parameters to match to the FODO lattice of the downstream DTL. This 4-quadrupole transport section will transform a beam with Twiss parameters and to a beam having Twiss parameters and . The middle two focusing elements plus the three drift lengths comprise the - (quarter wave) transport. Quadrupole Q1, placed where and , adjusts while preserving the condition and is used to adjust the beam size at Q2 while the quarter wave transformer preserves the condition and . Quadrupole Q2 is used to obtain the final desired while again preserving the condition . Because of the time varying nature of the RFQ, the and beams have the relationship , and at the exit of the RFQ; but, in a dc quadrupole channel, the matched beam satisfies and . By setting , for both and at the end of the RFQ, the Brown-Servranckx [1] matching transformer can be used for matching.

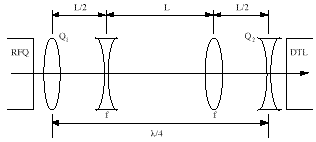
The quarter-wave transport matrix, , is (the sign of the focal length depends on the charge of the hydrogen ion)

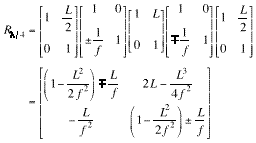(1)

which, in terms of the phase advance per period, m, and the Twiss parameters, is

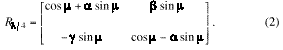. (2)

Equation (2) for the quarter wave transport system is

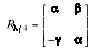(2a)

where m = 90o. This condition is achieved in Eq. (1) when

(3)

which determines the focal length, f, of the inner two quadrupole lenses given the lens separation, L. We require a transport matrix that preserves the condition . The Twiss parameter map for any matrix R is

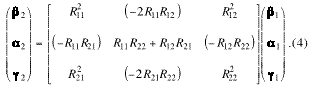. (4)

The matrix elements in parenthesis change sign in going from the x-plane to the y-plane. The other elements do not change sign. For and , then and . This is achievable with the quarter-wave transport system because the diagonal matrix elements and change signs between the x- and y-planes while the off-diagonal matrix elements and do not change. The quadrupole lenses placed at the beginning and end of the quarter-wave transport preserve the condition . The transport matrix elements for a single lens,

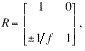, (5)

when substituted in Eq. (4), gives

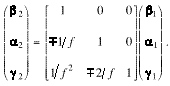. (6)

When and , then and .

The Brown-Servranckx transport system is straight forward to tune. Given a circular beam at the location of quadrupole Q1 in Fig. 1, the focal length of the middle two quadruples is adjusted to produce a circular beam at the location of quadruple Q2 giving a quarter wave transport between Q1 and Q2. Quadrupole Q1 is then adjusted to give the proper beam size at the location of Q2 (giving ). Finally, quadrupole Q2 is adjusted so that the beam size is a constant after each FODO cell of the DTL (giving the correct ). There are limitations to the degree of magnification that can be achieved by this transformer. The Twiss parameter has a minimum value equal to . For details of this and other useful insights to beam transport, see Ref. 1. If the transverse focusing per unit length is identical at the output of the RFQ and the input of the DTL, the quarter-wave transport can be eliminated. Also, if in addition to the above condition, at the RFQ output, a single magnetic quadrupole can be used to obtain the appropriate matching () of both and beams into the DTL.

[1] K. L. Brown and R. V. Servranckx, "First- and Second-Order Charged Particle Optics," SLAC-PUB-3381, July 1984.[2] K. Crandall, "Ending the RFQ Vane Tips with Quadrupole Symmetry," 1994 Linac Conference, Tsukuba, Japan.

*Work supported by the U.S. Department of Energy