M. Cavenago
INFN-LNL, via Romea n 4
I-35020 Legnaro (PD) Italy
The partly built line of the ECR ion source Alice, mainly based on electrostatic elements, needs several optimizations for different ion beam (A/q ranges from 2 to 9). Numerical codes easy to maintain and fast to execute were in demand. Beam optics codes are usually implemented as a kind of object oriented programs followed by a purposely written high level interpreter. This level was here replaced by general programs, combining symbolic and numerical capability, which therefore support different programming styles and a much finer physical description. Highly efficient linear tracking of electrostatic elements was obtained combining piecewise analytical solutions for quadratic and linear elements; some basic formulas and a sample result for Alice line are shown. Extension of elements to nonlinear case is given here, with detail for the anode lens.
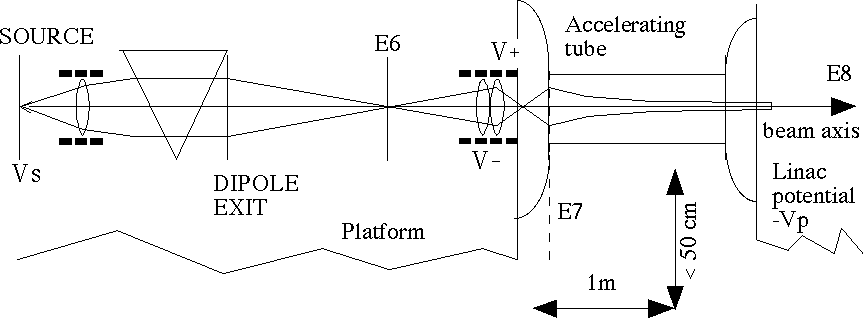
The beam transport system of the ECR [1] ion source Alice is mainly constituted by electrostatic elements (extractor, three einzel lens and the accelerating column), with one magnetic dipole for charge selection (Fig. 1). Due to the relative importance of fringing fields, our need for a flexible and easily adaptable matrix tracking code was apparent; nonlinear effects were also considered a second goal. We wrote some application programs, executed (interactively) by Mathematica [2]. Usual formulas for sources, drifts, thin lens and dipoles were easily implemented, as well as graphic capabilities. This paper describes the nontrivial approximations and equations that we used in simulating round electrostatic elements in some detail.
Paraxial analysis of einzel lens was indeed possible, by decomposing the lens
in seven regions
(or elements), where the axial field ![]() is assumed either constant (linear
elements) or linearly increasing (quadratic elements) [3].
Use of more than three regions allows a closer fit to actual fields.
A noteworthy nonlinear approximation (nonlinear means applicable
to nonparaxial rays), namely the Piecewise Quadratic
Approximation (PQA) is first introduced and briefly discussed;
matching between linear and quadratic element is extended
off-axis, allowing region boundaries to make a
is assumed either constant (linear
elements) or linearly increasing (quadratic elements) [3].
Use of more than three regions allows a closer fit to actual fields.
A noteworthy nonlinear approximation (nonlinear means applicable
to nonparaxial rays), namely the Piecewise Quadratic
Approximation (PQA) is first introduced and briefly discussed;
matching between linear and quadratic element is extended
off-axis, allowing region boundaries to make a ![]() angle
with z axis and introducing fictitious charges on element boundaries.
We apply this general
concept to anode lens effect.
angle
with z axis and introducing fictitious charges on element boundaries.
We apply this general
concept to anode lens effect.
We follow SI units in the code (generally) and use nonrelativistic mechanics, as suitable for ion sources. Since orbits do not depend on mass and charge in electrostatic fields, in section 2 and 3 we set unit mass and charge e=m=1 for brevity.
Let E be the total particle energy, a constant of motion, valid
for every element of our beamline.
First, we review the quadratic element. Consider a vacuum region where
the electrostatic potential ![]() is exactly:
is exactly:
![]()
Hamiltonian separates as ![]() with
with ![]() ,
whose value
,
whose value ![]() is a constant of motion; also the value of
is a constant of motion; also the value of ![]() is
the constant of motion
is
the constant of motion ![]() . Solving motion equations and
eliminating t in favour of z we write the motion from
. Solving motion equations and
eliminating t in favour of z we write the motion from ![]() to
to ![]() as
as
![]()
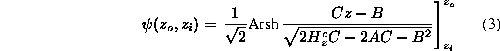
with ![]() . From these
nonlinear formulas
a linear approximation in
. From these
nonlinear formulas
a linear approximation in ![]() is obtained by putting
is obtained by putting
![]() in eq. (3). In case C<0 analytic continuation is taken.
Case C=0 is the linear element.
in eq. (3). In case C<0 analytic continuation is taken.
Case C=0 is the linear element.
The potential of einzel lens ![]() can be fitted by elements
like eq. (1) on intervals of z axis r=0; interval borders
can be fitted by elements
like eq. (1) on intervals of z axis r=0; interval borders ![]() are called
breaking points here.
In present code, we find convenient to use the well-known approximation
for symmetrical einzel lenses [3] :
are called
breaking points here.
In present code, we find convenient to use the well-known approximation
for symmetrical einzel lenses [3] :
![]()
with ![]() where R is the radius of electrodes
and
where R is the radius of electrodes
and ![]() ,
, ![]() their faces;
in perspective, also the potential
their faces;
in perspective, also the potential ![]() numerically computed (by POISSON) and adequately interpolated can
be fitted by the same elements.
numerically computed (by POISSON) and adequately interpolated can
be fitted by the same elements.
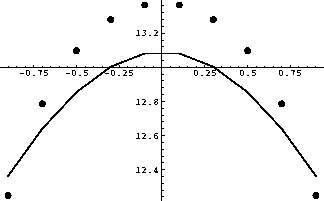
Elements are easily
counted by plotting (see Fig. 2a) the second derivative ![]() and
associating a C>0 element to some maximum (region III)
and a C<0 element
to some minimum (region I)
or low plateau. Between these elements, a C=0 element (region II)
will certainly improve matching. At z=0 we can include a C=B=0
element (region 0) or not, depending on lens dimension
and
associating a C>0 element to some maximum (region III)
and a C<0 element
to some minimum (region I)
or low plateau. Between these elements, a C=0 element (region II)
will certainly improve matching. At z=0 we can include a C=B=0
element (region 0) or not, depending on lens dimension ![]() .
In these regions,
potential elements on axis are better written:
.
In these regions,
potential elements on axis are better written:
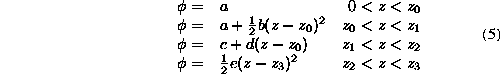
and ![]() for
for ![]() . Imposing continuity of
. Imposing continuity of
![]() and
and ![]() everywhere, we get
everywhere, we get
![]() ,
, ![]() and
and
![]() .
.
We choose
![]() to exactly reproduce the field at lens middle .
The remaining parameter
to exactly reproduce the field at lens middle .
The remaining parameter ![]() ,
, ![]() ,
, ![]() (breaking points)
and d
can be
determined by fitting
(breaking points)
and d
can be
determined by fitting ![]() to the actual potential
to the actual potential ![]() , that is by
minimizing the norm
, that is by
minimizing the norm
![]()
where ![]() and L is long enough (
and L is long enough ( ![]() suffices).
Considering also the second derivative is essential for
sound results of the fit, even if weights
suffices).
Considering also the second derivative is essential for
sound results of the fit, even if weights ![]() and
and ![]() may be varied; we choose
may be varied; we choose ![]() .
Note that
.
Note that
![]() is our criterion to
drop region 0, which case leaves five intervals in total instead of seven.
is our criterion to
drop region 0, which case leaves five intervals in total instead of seven.
In the paraxial approximation we can take region boundaries as ![]() planes, and extend potential off-axis according to (1). Indeed, at any
planes, and extend potential off-axis according to (1). Indeed, at any ![]() ,
,
![]() is discontinuous, so that a
is discontinuous, so that a ![]() discontinuity in
potential arise; this term may be neglected in paraxial approximation.
discontinuity in
potential arise; this term may be neglected in paraxial approximation.
To apply the quadratic elements in nonparaxial case, imagine to
have matched the potential ![]() and field
and field ![]() on axis at
breaking point
on axis at
breaking point ![]() between two element intervals;
to fix ideas, let
between two element intervals;
to fix ideas, let ![]() . The two elements are
. The two elements are
![]() and
and
![]() , with A and B equal
because of matching for r=0. Requiring potential continuity
, with A and B equal
because of matching for r=0. Requiring potential continuity
![]() implies
implies
![]()
These two lines (in fact cones)
are the element boundaries and separate three regions;
in region III we may have another element as eq. (1) with a different
![]() if desired.
if desired.
Matching ![]() off-axis is not possible. Discontinuity of
off-axis is not possible. Discontinuity of ![]() is equivalent to a charge (say positive), which implies a balancing charge
(negative) to be
located at lines (7). More quantitatively,
is equivalent to a charge (say positive), which implies a balancing charge
(negative) to be
located at lines (7). More quantitatively, ![]() be the true potential
(
be the true potential
( ![]() the true field),
the true field), ![]() our collection of elements
(so that
our collection of elements
(so that ![]() is a part of the electric field) and
is a part of the electric field) and ![]() the correction (localized near eq. (7) lines )
that restores matching between elements.
From Laplace eq.
the correction (localized near eq. (7) lines )
that restores matching between elements.
From Laplace eq. ![]() we indeed get:
we indeed get:
![]()
From eq. (7), boundaries associated to different ![]() may intersect at
may intersect at
![]() ,
which determines the maximum radius of validity of our element
decomposition.
,
which determines the maximum radius of validity of our element
decomposition.
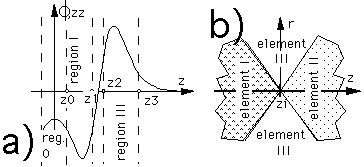
Non paraxial analysis is more easily applied to the
remarkable case of the anode lens
[4],
a hole of radius R in a conducting metal sheet (at ![]() )
separating a semispace
z<0 with field
)
separating a semispace
z<0 with field ![]() for
for ![]() from a semispace z>0 with field
from a semispace z>0 with field ![]() for
for ![]() .
Our field elements are explicitly
.
Our field elements are explicitly
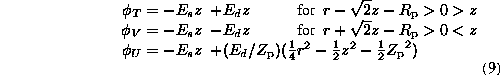
elsewhere, with ![]() . Here
. Here
![]() is a parameter; breaking points are
at
is a parameter; breaking points are
at ![]() . Choosing
. Choosing
![]() gives the exact values for
gives the exact values for ![]() , similarly
to einzel lens [4].
, similarly
to einzel lens [4].
From (9) we can compute the fictitious charge of (8):
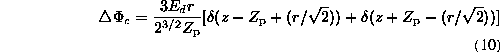
The effect of ![]() on particle motion
can be approximately described by a (small)
transverse kick
on particle motion
can be approximately described by a (small)
transverse kick ![]() when passing boundaries; for example
crossing T-U boundary gives
when passing boundaries; for example
crossing T-U boundary gives
![]()
where ![]() are r,z at the crossing;
are r,z at the crossing; ![]() is
is ![]() at
this time;
at
this time; ![]() is
is ![]() at this time. Component
at this time. Component ![]() is such
to maintain energy unchanged. This kick does not contribute to linear
focusing, but to aberations.
is such
to maintain energy unchanged. This kick does not contribute to linear
focusing, but to aberations.
We can now formulate a fast tracking for the anode lens. For convenience we project initial and final states on z=0. The initial motion:
![]()
with ![]() is therefore parameterized
by
is therefore parameterized
by ![]() , which would be the values of
, which would be the values of
![]() at z=0 ,
if our particle would propagate in a constant field
at z=0 ,
if our particle would propagate in a constant field ![]() up to there.
From (12) and boundary eq.
up to there.
From (12) and boundary eq. ![]() crossing values
crossing values ![]() can be easily determined.
After crossing we have
can be easily determined.
After crossing we have ![]() with the kick (11).
Motion follows eq. (2) up to crossing with U-V boundary, at
with the kick (11).
Motion follows eq. (2) up to crossing with U-V boundary, at
![]() ;
; ![]() is determined by
is determined by
![]()
which can be solved iteratively. A good starting value for ![]() is
is ![]()
![]()
with ![]() .
Final value of
.
Final value of ![]() is
is ![]() where the second kick
is given by eq. (11), with
where the second kick
is given by eq. (11), with ![]() replaced by
replaced by ![]() (and similar replacement
for
(and similar replacement
for ![]()
![]()
![]() ).
).
As a general remark, programs become more involved with their size; in our opinion, no recipe can guarantee order and clarity (and absence of error). It is then natural to break a program into several parts, mainly a ``physics part'' [5], where formula as (1)-(14) are coded as plainly as possible, and an ``interpreter'', ultimately relating with numbers and graphics; for example, as COSY and FOXY (interpreting COSY to Fortran [5]). Our try in this direction is the use of an external interpreter, at present Mathematica [2]; advantages of this approach are more evident at the beginning (as now), when the physics code is small enough to make errors unlikely; and reformulation is possible.
A Mathematica applicative program (code in brief) consists of definition of
transformation of symbols, with possibility of delaying or conditioning
their execution: almost any kind of programming style is possible.
It is probable that object programming, implemented by
``UpSetDelayed'' [2], will be a fairly good recipe to order
information about the several treated objects: dipoles, regions of einzel
lenses
or of accelerating tubes, drifts. At present, a traditional
style was used: an element is a list, including the element name,
kind of approximation used, and parameters. For example,
![]() dipolex,fringe,
dipolex,fringe, ![]() in
in ![]() out
out ![]() represents H.Enge's model of dipole [4]. Simbols ``matrix2''
and ``matrix3'' represent actions on
represents H.Enge's model of dipole [4]. Simbols ``matrix2''
and ``matrix3'' represent actions on ![]() phase-space and
phase-space and ![]() space respectively. An einzel lens is converted
into a sequence of seven lists.
A beamline is a list of lists, on which a traditional
loop
distributes the action of ``matrix3''. Operation on lists
may be more concisely done with in-built symbols ``Thread'' and ``Map'',
in an advanced style.
Graphics rendering was very flexible and satisfying.
We plan to merge fitting of elements to einzel into some
post-processor of Poisson equation numerical solvers.
space respectively. An einzel lens is converted
into a sequence of seven lists.
A beamline is a list of lists, on which a traditional
loop
distributes the action of ``matrix3''. Operation on lists
may be more concisely done with in-built symbols ``Thread'' and ``Map'',
in an advanced style.
Graphics rendering was very flexible and satisfying.
We plan to merge fitting of elements to einzel into some
post-processor of Poisson equation numerical solvers.
Let ![]() be the voltages of the three einzel lenses,
be the voltages of the three einzel lenses,
![]() be the source
voltage and
be the source
voltage and ![]() be the linac voltage, referenced to platform.
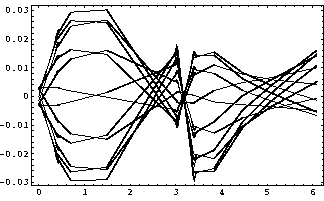
Fig. 3a) was computed for a beam of He
be the linac voltage, referenced to platform.
Fig. 3a) was computed for a beam of He ![]() ,
setting
,
setting ![]() kV, (i.e.
kV, (i.e. ![]() keV),
keV),
![]() kV for the
first einzel
and optimizing
kV for the
first einzel
and optimizing ![]() kV;
a
kV;
a ![]() V perturbation was added.
Simulation for Ar
V perturbation was added.
Simulation for Ar ![]() and U
and U ![]() beams
proved even better transport, provided that
latter voltages (and intermediate waists)
are changed:
beams
proved even better transport, provided that
latter voltages (and intermediate waists)
are changed: ![]() kV and (0,6.3,314)
kV respectively . Fig 3b) shows
that also aberration
can be reproduced by PQA, in fairly good agreement with RungeKutta
computations.
kV and (0,6.3,314)
kV respectively . Fig 3b) shows
that also aberration
can be reproduced by PQA, in fairly good agreement with RungeKutta
computations.