A description of different types of the accelerating
structures that have been studied and constructed in NSC KIPT
for electron linacs during last years is given in this paper.
The accelerating structures consist of the inhomogeneous disk-loaded
waveguides and input and output couplers. The disc-loaded waveguides
operate at 2797 MHz in
mode and have different laws of variation of the disk apertures.
Before brazing cups were tuned with using special method. This
method is discussed in this paper.
During development and tuning of linac accelerating sections, based on homogeneous disk-loaded waveguides, widely used are various cavity stacks, shorted at each end or at only one (plunger method) (see, for example, [1]). In case of homogeneous structures, the possibility of their employment for E-modes is based on the fact that in the infinite periodic waveguide there exists for E-modes an infinite number of symmetry planes whose replacement with metal planes does not affect the field structure. For such short-circuiting, despite the fact that only the finite number of cavities are involved in the cavity stack, the characteristics of the both traveling waves ( into which the standing wave of the stack can be expanded) are completely identical to those of the wave propagating through infinite (or matched at the ends) waveguide.
A more complicated is the case of inhomogeneous disk-loaded waveguides for which the periodicity condition is violated and, strictly speaking, the grounds disappear not only for utilization of cavity stacks, but for existence of traveling waves which are synchronous with charged particles. If the disk-loaded waveguide parameters vary slowly along the waveguide, then, the amplitudes of reflected waves are small, and in the system there is a traveling wave with slow-varying parameters. Tuning of such waveguides, using cavity sets, is performed with a low systematic error which is proportional to the inhomogeneity value. As far as the possibility of using for acceleration (generation, amplification) purposes disk-loaded waveguides with highly variable parameters, in each specific case, there is necessity to analyze the types and structures of waveguide fields and, then, develop techniques for tuning the components of this slow-wave structure. In general case, there are no stringent laws which could guarantee one or another property of the inhomogeneous structure, as different from homogeneous ones.
One more requirement imposed on the cavity stacks is the possibility of a consecutive tuning (i.e., a selection the geometrical dimensions one way or another) of waveguide cells. In case of cavity stacks, which model the homogeneous disk-loaded waveguides, this requirement is fulfilled automatically: when one has tuned K cells he can tune (K+1)-cell. In case of inhomogeneous structures, such condition becomes realizable depending upon the degree of coupling between different resonators that form the disk-loaded waveguide.
The calculations performed by us on the base of a
new disk-loaded waveguide model (coupled cavity chain) [2] indicate
that for waveguides with the period ,
where
is the free-space wavelength, the
"remote" coupling influences weakly on the phase-shift
per cell. For
, taking into account the
"cross-cavity coupling" ((i, i-1), (i, i+1),
(i-1, i+1), i - is the cavity number) at
(
- is the coupling hole radius), one
can expect to achieve an accuracy of forming a phase-shift per
cell of the order of
. If one restricts
oneself only "paired coupling" ((i, i-1), (i, i+1)),
then, the accuracy of phase-shift per cell is getting worse -
. Development of the techniques of disk-loaded
waveguide cell tuning that should allow to make feasible the cross-cavity
coupling is a difficult task, since during tuning of the i-th
resonator one has to take into account, somehow, the effect from
the (i+1)-th resonator which has not yet been tuned.
This paper presents the results of our research on
the technique of cell-tuning in a strongly inhomogeneous disk-loaded
waveguides which realizes paired coupling.
From the paper [2] it follows that an infinite chain
of cylindrical cavities of the length
and the radii
, coupled through co-axial
cylindrical holes with the radii
in the
cavity dividing walls with the thickness
(inhomogeneous
disk-loaded waveguide with the period
)
at
can be, with a definite accuracy,
described by a set of coupled equations
(1)
where - are the amplitudes
of
-modes in the n-th cavity,
- is the n-th cavity eigen frequency,
- are the relative n-th cavity eigen frequency shift due to coupling
with (n+1) and (n-1) cavities,
-are the
coupling coefficients. If
and
are determined by geometrical dimensions of only the n-th and
(n+1)-th cavities, as well as by the coupling hole radius
(
are determined by geometrical dimensions
of the n-th, (n-1)-th cavities and the hole radius
),
then we shall say that the cavity coupling is paired. If these
coefficients depend on geometrical dimensions of three cavities
(n-th, (n+1)-th and (n-1)-th), as well as two coupling hole radii
, then, such coupling we shall call "cross-cavity
coupling".
Let's find the conditions, when the set (1) at
(
- is the operating frequency) has the
solution of such form
, where
- is the real value. From (1) it follows that in order to achieve
this, the following conditions is to be fulfilled
For the n-th cavity (1) will take on the form
(2)
and for the (n-1)-th cavity
(3)
From (2) and (3) it follows that, if
is independent from the parameters of the (n+1)-th cavity,
- from the parameters of the (n-2)-th
cavity and
depend only upon the parameters
of the n-th and (n-1)-th cavities, then, two equations (2) and
(3) become closed and determine fully the relation of geometrical
dimensions of the n-th and (n-1)-th cavity. In this case, having
tuned the (n-1)-th cavity, one can find the conditions which must
satisfy the geometrical dimensions of the n-th cavity, and, consequently,
allow to consecutively tune all waveguides cavities. It can be
shown that at the paired coupling
and
these coefficients are determined by the geometrical dimensions
of the n-th and (n-1)-th cavities, only. Things are more complicated
with the dependence of coefficients
on
the parameters of the (n+1)-th cavity and
on the parameters of the (n-2)-th cavity. Even under the assumption
of paired coupling such dependence exists. However, our calculations
shown that this dependence is considerably weaker than the dependence
on the parameters of the n-th ((n-1)-th) cavity, and can be neglected,
as a result.
From the equations (2) and (3) it follows that in
order to achieve the traveling wave mode in an inhomogeneous disk-loaded
waveguides with the mode type it is necessary
that the parameters of the (n-1)-th and the n-th cavities be connected
via the relationship
(4)
Suppose we have placed the n-th and (n-1)-th cavity
into some sort of a cavity stack. It can be shown that the conditions
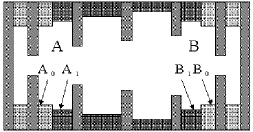
(4) is fulfilled in the case, when in the cavities A and B (see
Fig.1),adjoining the cells under consideration, the amplitudes
of -modes equal to zero. For cavity stacks,
shorted at both ends, this condition can be accomplished by coupling
the cavities A and B to terminal cavities, resonance-tuned at
the frequency
with taking into account
the frequency shift due to the hole effect. Such cavity stacks
have already been used for tuning separate parts of quasi-constant
impedance sections for LIL accelerator [3]. However, there the
cells were tuned not consecutively , i.e. beginning from the entrance
(or exit), but in different stacks being then simply joined one-to-one.
The above results indicate that it is possible to
use a consecutive tuning of all cells for disk-loaded waveguides
with an arbitrary law of the coupling hole radius variation. With
that, at the operating frequency the
traveling wave mode with the phase shift on the order of
with a certain accuracy is guaranteed in a waveguide. However,
a quite natural question arises about the characteristics of such
traveling wave, since the inhomogeneity in a disk-loaded waveguides
is created with the purpose of optimizing its characteristics.
Let's consider, for instance, a quasi-constant impedance section.
Such a waveguide is supposed to consist of several homogeneous
(
) segments with different radii of the
coupling holes and transition sells which provide the matching
of these segments. Our analysis indicates that fulfillment of
such a requirement is realizable only under a certain law (unknown
a priory ) of hole radius variation. If one use the disks in the
transition sells with some law of the hole radius variation (for
instance, the linear one) and consecutive tune all cavities following
the above technique, he can obtain a waveguide which will operate
in a traveling mode at
, but its segments
which are homogeneous relatively the hole radius will not be homogeneous
relatively the waveguide inside diameter. Thus, under application
of the above technique to the consecutive cell tuning in the case
of the linear law of hole radius variation in the transition sells,
the waveguide inside diameter will be periodically change within
the second segment, i.e. the second segment of the section will
be bi-periodic. For the subsequent "homogeneous" segments
the law of the waveguide inside diameter variation will be more
complicated. In the case of the linear law of hole radius variation
in the transition sells two homogeneous segments cannot be matched
together without violation of the condition
.
and the precise matching is impossible and from the transition
there occur certain reflection with a small phase jump. What is
more expedient for the accelerating section: the traveling wave
mode with cavity frequency variation along the length of the structure,
and, consequently, with the acceleration amplitude variation causing
a certain decrease in the energy gain or a joining of segments
with a small phase jump and reflection that, also, leads to a
certain decrease in the energy gain? There is no unambiguous answer
to this question. In each case one will have to analyze the energy
gain (or other characteristics) with taking into account the above
factors. Our calculations indicate, for instance, that in the
case of a structure with two homogeneous segments and for the
linear law of hole radius variation in the transition sells more
preferable would be the situation with the periodic cavity frequency
variation in the second segment from the standpoint of energy
gain.
Consecutive tuning feasibility is determined by stability
of the technique, as well. The numerical analysis indicates that
small errors in the tuning of individual cells should not lead
to the exponential growth of subsequent deviations, i.e. the technique
must be stable.
The National Science Center "Kharkov Institute of Physics&Technology" (NSC KIPT) has created a technological base for building accelerating structures on the base of disk-loaded waveguides. The basic elements of a disk-loaded waveguides is asymmetric cell ( disk and cup). The high-precision copper cups and disks are made on diamond tool lathers. Prior to brazing, the cups are tuned using different cavity stacks. Brazing a segment of cups and irises, segments and couplers are made in a vacuum RF-furnace at 779C using the KIPT technology.
We have developed and manufactured four short inhomogeneous
accelerating sections with and
,
three of which (S1, S2, S3) have quasi-constant law of coupling
hole radius variation with a linear decrease of radii in transition
cells, while in the fourth one (S4) the coupling hole radii decrease
linearly from entrance to exit. Calculated characteristics of
the first three sections are given in Table 1.
Prior to brazing the first section sells were tuned
using the method completely coinciding with the one presented
in [3]. Cavities in the second, third and fourth sections were
consecutively tuned in the cavity stack using the above described
method. While doing so, as compare with [3], the number of auxiliary
cells was reduced to the minimum - we used only four auxiliary
cells (see Fig.1). Cells A and B were composite ones (A=A1+A0,
B=B1+B0, A0=B0)
and during tuning process cells A0 and B0
were unchanged while the radii of cells A1 and B1
were changed according to a certain law. For sections S2 and S3
the radii of cells A1 and B1 were changed
after tuning the transition sells, for section S4 - they were
consecutively tuned together with the main sells. After brazing
the sections cells were tuned by way of a small external deformation
of the cups until the needed phase shift was achieved ()
during the shorting plunger movement. Since such a tuning cleaned
away all the errors of the first tuning (before brazing) we did
not see the difference in the characteristics between sections
S1, S2 and S3.
| ||
| Frequency, MHz | ||
| Input Power, MW | ||
| Energy Gain, MeV | ||
| Beam Power, MW | ||
| Gradient, Mev/m | ||
| Section Length, m | ||
| Filling Time, sec | ||
| Field Attenuation, Nep/sect. |
| |
| Output Power, MW | ||
| Number of Homoge-neous Segments (Iris Diameters, mm) | ||
During measurements of the after-brazing phase shifts
it was found that the operating frequency of all sections was
150 to 200 kHz lower than the calculated one. It can be explained
as errors of used cavity stack. Indeed, the above stacks are just
for paired cavity coupling. According to the results of our calculations
[2] the negligence of the "remote" coupling can produce
errors during tuning about which agrees
in value and sign with the obtained deviation of the operating
frequency.
The section S1 was installed on KUT accelerator [4]. The results of beam characteristics measurements agreed with simulations.
Thus, our R&D has shown that the feasibility
is there to tune (with a certain error) of disk-loaded waveguides
with arbitrary law of hole radius variation. In order to achieve
the necessary characteristics the choice of such law must be made
with taking into account both the properties of inhomogeneous
waveguides as the feasibility of tuning such waveguides. In view
of all the above-said, a procedure should be worked out to optimize
the structures considered. At present, based on the approach [2]
we have begun to investigate this problem.
The authors wish to thank A.N.Dovbnya, V.A.Kushnir
and V.V.Mitrochenko for discussions relating results of this work.
[1] O.A. Valdner, N.P. Sobenin, I.S. Zverev et al. Disk Loaded Waveguides. Reference Book. Moscow, Energoatomizdat, 1991.
[2] M.I.Ayzatsky. New Mathematical Model of an Infinite Cavity Chain, Proc. EPAC96, will be published.
[3] Bienvenu G., Bourdon JC, Brunet P. et al. Accelerating Structure Developments for the LEP Injector Linac. Proceedings of the 1984 Linear Aceelerator Conference. GSI-84-11. p. (1984)
[4] M.I.Ayzatsky, Yu.I.Akchurin, V.I.Beloglazov et al. KYT - Industrial Technological Accelerator, Proc.XIV Particle Accelerator Workshop, Protvino, v.4, p.259 (1994)