J.P. Pruiksma, R.W. de Leeuw, J.I.M. Botman ![]() , H.L. Hagedoorn,
Cyclotron Laboratory
, H.L. Hagedoorn,
Cyclotron Laboratory
A. G. Tijhuis, Electromagnetics Department,
Eindhoven University of Technology,
P.O. Box 513, 5600 MB Eindhoven, the Netherlands
An analytical description of the electromagnetic field in a periodically disk-loaded circular waveguide is given. The field is expressed in terms of the waveguide modes. The main advantage of this approach is that each mode matches the boundary conditions in the empty waveguide. These modes have convenient orhogonality properties. First, a single diaphragm in the waveguide is considered and the reflection problem arising from one incident waveguide mode is solved with the mode-matching technique. Then a matrix eigenvalue equation is derived for the periodically loaded waveguide. The solution of this equation yields the dispersion curve for the structure and leads to the full field description for a given operating mode of the accelerator.
A circular waveguide of radius b, centered around the z-axis is considered.
For the acceleration of particles in the disk-loaded waveguide, only the
transverse magnetic (TM) modes of the electromagnetic field are of interest.
A time dependence of ![]() and a z dependence of
and a z dependence of ![]() is assumed and substituted into Maxwell's equations. The axially symmetric
is assumed and substituted into Maxwell's equations. The axially symmetric
![]() mode solutions are:
mode solutions are:
For the nth mode, the z-component of the electric field is ![]() , the
radial electric field- and azimuthal magnetic field components are
, the
radial electric field- and azimuthal magnetic field components are ![]() and
and ![]() respectively. The wave admittance
respectively. The wave admittance
![]() and
and ![]() is the nth root of
the Bessel function
is the nth root of
the Bessel function ![]() . The functions
. The functions ![]() defined in equation
(2) are orthonormal:
defined in equation
(2) are orthonormal:
![]()
The mode-matching technique discussed in the next section makes use of this
orthonormality.
For linear travelling wave accelerating structures it is customary to choose
the radius b and the frequency ![]() in such a way that only the propagation
constant
in such a way that only the propagation
constant ![]() is imaginary. All other {
is imaginary. All other { ![]() } are real and represent
attenuating modes.
} are real and represent
attenuating modes.
In the circular waveguide of radius b, an infinitely thin diaphragm with a circular aperture of radius a is placed at z=0, see figure 1.
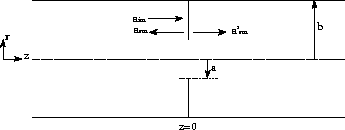
The coefficients of the incident modes are ![]() so a general incident field
is given by:
so a general incident field
is given by:
Here, the reflection problem is solved for one incident propagating mode:
![]() and all other
and all other ![]() are zero. At the diaphragm, there
will be an infinite number of reflected and transmitted modes with coefficients
are zero. At the diaphragm, there
will be an infinite number of reflected and transmitted modes with coefficients
![]() and
and ![]() respectively, because at z=0 a linear combination of
all the modes is needed to satisfy the boundary conditions at the diaphragm.
The total radial electric field
respectively, because at z=0 a linear combination of
all the modes is needed to satisfy the boundary conditions at the diaphragm.
The total radial electric field ![]() and azimuthal magnetic field
and azimuthal magnetic field
![]() are:
are:
For z<0:
For z>0:
By using the boundary condition ![]() at the diaphragm for a<r<b and
the continuity of the tangential field components in the aperture (z=0):
at the diaphragm for a<r<b and
the continuity of the tangential field components in the aperture (z=0): ![]() and
and ![]() for
for ![]() , a matrix equation can be derived, whose
solution yields the coefficients
, a matrix equation can be derived, whose
solution yields the coefficients ![]() and
and ![]() . In the derivation,
the orthonormality of the
. In the derivation,
the orthonormality of the ![]() functions is used. This procedure is known
as the mode-matching technique, see Masterman [1].
functions is used. This procedure is known
as the mode-matching technique, see Masterman [1].
To obtain a matrix equation of finite size, the series of reflected and
transmitted modes have to be truncated; therefore only a finite number of
coefficients are calculated. Once the coefficients ![]() and
and ![]() are
found, the total field can be calculated at every position in the waveguide.
The most important coefficients are
are
found, the total field can be calculated at every position in the waveguide.
The most important coefficients are ![]() and
and ![]() . These are better
known as the reflection coefficient R and transmission coefficient T. The
coefficients are in general complex numbers, and as a measure for R, the
susceptance B is defined as:
. These are better
known as the reflection coefficient R and transmission coefficient T. The
coefficients are in general complex numbers, and as a measure for R, the
susceptance B is defined as:
![]()
B is a real-valued quantity [2]. The susceptance B has been calculated as a function
of the frequency ![]() , see figure 2.
, see figure 2.
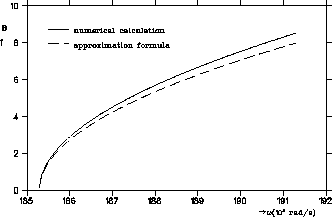
The solid line is calculated by using the mode-matching technique and the dashed line represents an approximation for the susceptance given by an analytical formula derived with the small-aperture theory [3]:
where ![]() . This formula was derived by assuming that the aperture
diameter is small compared to the guide wavelength
. This formula was derived by assuming that the aperture
diameter is small compared to the guide wavelength ![]() .
Calculations for smaller aperture radii show an even better agreement between the
mode-matching solution and the approximation formula [2].
.
Calculations for smaller aperture radii show an even better agreement between the
mode-matching solution and the approximation formula [2].
In figure 3, a section of an infinitely long periodic structure is shown. The structure consists of an empty waveguide with radius b, containing diaphragms with aperture radius a, equally spaced at a distance d.
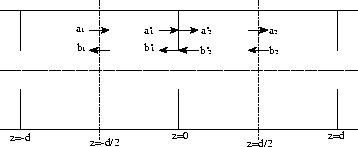
It is assumed that the decaying modes excited at the diaphragms decrease
to a negligible value at the neighbouring diaphragms and that only the
reflected and transmitted propagating mode is of importance [2].
Once the coefficients for the back and forth propagating modes are found, the
coefficients of the decaying modes can be calculated from the single-diaphragm
theory discussed in the previous section.
The radial electric field of the propagating modes is:
For -d<z<0:
![]()
For 0<z<d:
![]()
Similar equations can be found for the azimuthal magnetic field.
In the expression for ![]() , the term
, the term ![]() represents the field of the mode propagating in the positive z-direction.
When
represents the field of the mode propagating in the positive z-direction.
When ![]() is seen as an effective coefficient for this mode, the
coefficient at the diaphragm (z=0) is
is seen as an effective coefficient for this mode, the
coefficient at the diaphragm (z=0) is ![]() , see figure 3.
The coefficient at
, see figure 3.
The coefficient at ![]() is called
is called ![]() and is given by:
and is given by:
The other coefficients are defined in a similar way. The coefficients ![]() and
and ![]() are linked to
are linked to ![]() and
and ![]() in the following way:
in the following way:
By using equations (16) and (17) together with equation
(15) and similar equations for the other coefficients, a transfer
matrix can be found which connects the coefficients ![]() and
and ![]() at
at
![]() with the coefficients
with the coefficients ![]() and
and ![]() at
at ![]() :
:
The Floquet theorem, see Collin [3], links the fields at
position ![]() to the fields at position
to the fields at position ![]() :
:
where ![]() is the phase shift per cell.
With this equation, a phase velocity can be defined, because at the time
is the phase shift per cell.
With this equation, a phase velocity can be defined, because at the time
![]() the fields at z+d are the same as the fields at position
z for t=0. This gives a phase-velocity:
the fields at z+d are the same as the fields at position
z for t=0. This gives a phase-velocity:
![]()
By combining equations (18) and (19), a matrix eigenvalue equation can be derived, which has the characteristic equation:
With B the susceptance. From equation (21) it can be observed that
the phase shift per cell ![]() can also be negative, which yields a
solution for waves travelling in the negative z-direction.
can also be negative, which yields a
solution for waves travelling in the negative z-direction.
Since B has been calculated as a function of ![]() and k is also known
as a function of
and k is also known
as a function of ![]() from equation (4),
from equation (4),
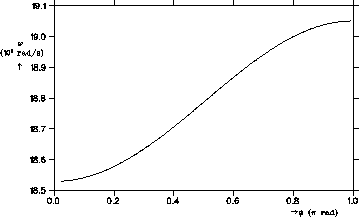
the phase shift per cell ![]() can be calculated as a function of
can be calculated as a function of
![]() , see figure 4. This figure was made using the
parameters of the periodic structure of a 10 MeV linear travelling-wave
electron accelerator with an operation mode
, see figure 4. This figure was made using the
parameters of the periodic structure of a 10 MeV linear travelling-wave
electron accelerator with an operation mode ![]() . From
figure 4, the frequency of this
. From
figure 4, the frequency of this ![]() mode can
be deduced. Once the frequency has been found, the eigenvalue problem can be
solved and the coefficients of the propagating modes are obtained. With these,
the coefficients of the decaying modes can be calculated by using the single
diaphragm theory. For a phase shift of
mode can
be deduced. Once the frequency has been found, the eigenvalue problem can be
solved and the coefficients of the propagating modes are obtained. With these,
the coefficients of the decaying modes can be calculated by using the single
diaphragm theory. For a phase shift of ![]() per cell, three cells
are needed for the field description. Figure 5 shows the total
longitudinal electric field on the z-axis in the three cells.
per cell, three cells
are needed for the field description. Figure 5 shows the total
longitudinal electric field on the z-axis in the three cells.
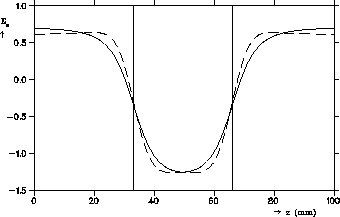
The empty waveguide modes are a useful tool for the description of the
electromagnetic field in periodically disk-loaded waveguides. With the
mode-matching technique, the reflection of waves from an infinitely thin
diaphragm is described accurately. The dispersion curve of the infinitely
long periodic structure can be calculated and the calculated fields for
a given frequency ![]() agree reasonably well with the fields calulated by
Superfish.
agree reasonably well with the fields calulated by
Superfish.
To obtain more accurate results, the theory could be extended to include
diaphragms of finite thickness [2] [5] and also to a
description of aperiodic structures [6], which is important for
the design of low-energy travelling-wave linacs.