A design for a split-coaxial, normally-conducting, 12 MHz RFQ structure is being developed to accelerate singly charged ions of mass 132 and heavier to a velocity v/c = 0.008, suitable for injection into the ATLAS superconducting heavy-ion linac. Numerical studies have shown that a transverse (normalized) acceptance of 0.25 mm-mrad can be achieved while maintaining a longitudinal emittance as small as a few keV-nsec. A novel feature is the use of drift-tubes at the entrance and exit of the RFQ which make use of the voltage offsets intrinsic to the split-coaxial structure to increase the voltage gain by about 30%. A half-scale model of the RFQ has been built and tested. The model, with no provision for cooling, was not operable cw but was pulsed to vane-vane voltages as high as 59 kV for periods of several milliseconds. The achieved level, limited by arcing in an rf feedthrough and so not a fundamental limit for the structure, corresponds to 1.2 times the (frequency and gap dependent) Kilpatrick limit. Assuming the model results scale, a 2 meter long 12 MHz RFQ, with 8 mm minimum aperture radius, will operate at 100 kV intervane voltage with an RF input of slightly less than 25 kW. Design and construction status of a full-scale prototype is discussed.

This paper discusses the ongoing development of a low-frequency RFQ as the initial element of a secondary beam linac for an ISOL-type radioactive beam facility. The proposed facility would upgrade the existing ATLAS superconducting heavy-ion linac for the acceleration of radioactive beams [1,2]. In its present form, ATLAS can accelerate any ion with a sufficiently high charge state (q/A > 0.1). For efficient production of most radioactive beams, much lower charge states must be accelerated, at least for the first few MV of the linac. Adapting ATLAS to radioactive beams, therefore, requires development of a low-charge-state injector which can maintain the good features of ATLAS, i.e. large transverse acceptance, flexibility in configuration, and most particularly, excellent beam quality [2,3]. To meet these goals, it is necessary to maintain substantially smaller longitudinal emittance than is typical for RFQ implementations. Several features of the RFQ discussed here ensure this result.

The RFQ should operate at as low a frequency as is practicable both to minimize longitudinal emittance growth and also to maximize the transverse acceptance. The split-coaxial RFQ geometry is appropriate for this frequency range; RFQ structures have already been developed that operate near the frequency and fields required[4].

Injecting the RFQ with a pre-bunched beam maintains the longitudinal emittance at a smaller value than is practicable using adiabatic bunching within the RFQ structure [5]. Also, by removing the bunching function, the length of the RFQ is reduced and the efficiency enhanced. A suitable bunching system exists: the 12 MHz gridded-gap, four-harmonic system which is presently in use on the ATLAS accelerator can bunch 70% of a dc beam into 1 nsec bunches[6]. The efficiency can be further improved by development of a finer grid structure, which should be straightforward for the very low beam currents anticipated.

Placing the RFQ on a variable voltage platform (350 kV) allows operation at a constant velocity profile for a wide range of ion masses and also increases the velocity at the entrance of the RFQ, thus increasing the transverse acceptance.

We have analyzed an RFQ structure configured for beams of charge to mass ratio of 1/132 [2]. Ions of higher charge state are accommodated by scaling the platform voltage to maintain a constant injection velocity and the RFQ voltage as the ratio of mass to charge. The RFQ parameters are as follows:

Operating frequency 12.125 MHz

Resonant Structure split-coaxial

Vane-vane voltage 100 kV

Maximum Electric field 12.8 MV/m (1.2 KP)

Minimum Aperture 8.00 mm radius

Modulation factor 1.5

Entrance Velocity 0.00247 c

Exit Velocity 0.00493 c

Number of cells 44

Length 222 cm

Synchronous phase -30 degrees

The split-coaxial structure is characterized by a voltage offset of _ the vane-vane voltage (V_v) at both entrance and exit. We make use of this offset to provide accelerating potential by attaching a drift tube to the high-voltage vane pair at both the entrance and exit of the RFQ. The energy gain provided by the two drift tubes is somewhat greater than twice V_v and, as shown below, increases the voltage gain through the RFQ by more than 20%.

The electric fields near the vane tips have been numerically modeled using TOSCA and also RELAX3D.

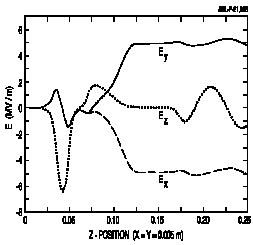
The vane geometry used has a constant radius of curvature of 10 mm, 1.25 times the minimum aperture radius. At entrance and exit the vanes are tapered over a 4 cm interval.

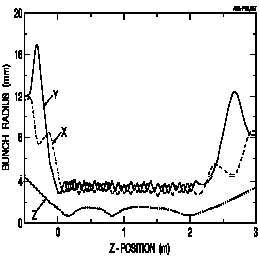
Figure 2 shows the transverse and longitudinal dimensions of a beam bunch numerically traced through the RFQ and includes matching electrostatic triplets at the entrance and exit. Some parameters for the beam shown are:

Species Sn¹³²

Charge state 1+

Entrance Velocity .00247 (378 keV)

Exit velocity .00493 (1508 keV)

Emittance (normalized)

Input:

Transverse 0.27 p mmmrad

Longitudinal 4.7 p keVnsec

Output:

Transverse 0.27 p mmmrad

Longitudinal 6.1 p keVnsec

The small increase in longitudinal emittance through the RFQ indicates that beam quality in this system will be determined primarily by the bunching system. It should be noted that the transverse acceptance projected above is substantially greater than required for the ISOL - type ion sources contemplated for this machine. In fact, for the vane voltage assumed above, it is possible to accelerate singly charged uranium ions and achieve similarly small longitudinal emittance values by reducing the RFQ modulation factor from 1.5 to 1.3, and the transverse acceptance from 0.27 to 0.17 p mmmrad.

An roughly half-scale model (19.6 MHz) of the RFQ, with unmodulated vanes, has been constructed of copper and aluminum. Measurements of the electromagnetic fields in the model yielded the following results (where we have scaled both the structure size and the observed RF surface resistance to 12.125 MHz) for V_v = 100 kV:

RF Input Power = 23.6 kW

Peak surface electric field = 12.3 MV/m

RF Energy = 2.3 joules

Even though no efforts at vibration isolation were made, the effects of ambient mechanical vibrations on the RF eigenfrequency were much less than the intrinsic resonator bandwidth and should pose no operational problem.

The model was so constructed that it was possible to evacuate the resonator and operate it at high fields. No provision for water cooling was made, however, so that high-field operation was limited to periods of a few milliseconds at a repetition rate of a few pulses per second.

An rf pickup loop to monitor the vane voltage was calibrated by three different methods. The first method, using the results of perturbation measurements of the field together with direct measurements of the rf energy content of the resonator, gave values for V_v in good agreement with a direct

measurement using a high-impedance probe. The third method was to observe the high-energy cutoff energy for bremstrahlung produced during high-field tests: this indicated voltages some 20% higher than the voltage determined by the two previously mentioned methods. This may be due to bremstrahlung resulting from electron trajectories which traverse an appreciable portion of the length of the RFQ while traveling between vane pairs. In the split-coaxial structure, such trajectories can yield voltages greater than V_v. The calibration for the results discussed here was from the first two methods discussed.

On operation following initial pumpdown, the structure exhibited low-level multipacting, which conditioned away in less than an hour. High power operation was with pulses of a few milliseconds duration, and with a duty factor less than 1%. At higher field levels, the structure arced between the RFQ vanes repeatedly but within a few hours had conditioned to V_v = 59 kV. At this level the input power was limited (at approximately 15 kW) by arcing in a vacuum feedthrough to the power coupling loop

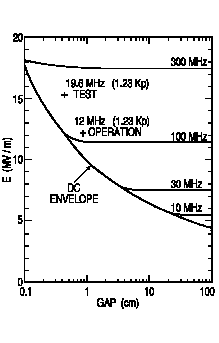
Figure 3 shows the results of this test, in the context of the Kilpatrick model for limiting electric fields in RF structures[7]. It should be noted that for most RFQ implementations, the rf frequency is sufficiently high that for practical vane-vane spacing, the Kilpatrick limit is in the asymptotic limit of large gap, and the gap dependence is generally ignored. For the present case of a very low frequency RFQ, however, we are not in the asymptotic region for the Kilpatrick model, and the gap dependence is quite important. This is born out by the experimental result for the 19 MHz model shown in Figure 3, which is nearly three times the asymptotic Kilpatrick limit for this frequency, but only 1.23 times the Kilpatrick limit when the gap dependence is included. Using the complete Kilpatrick model to scale the present result to a 12 MHz structure, it appears that operation at an intervane voltage of 100 kV is feasible.

By operating at low frequency, and by pre-bunching the beam, it seems feasible to provide good transverse acceptance and excellent longitudinal beam quality in an RFQ structure for singly-charged ions heavier than mass 132. It should be noted that two two-meter sections of 12 MHz RFQ will be required for an injector for ATLAS. This paper has focused on the critical entrance section, as subsequent sections are similar, but technically less demanding.

A two-meter section of 12 MHz RFQ is presently under construction. Tests are planned initially to be with unmodulated vanes, for the purpose of demonstrating cw operation and determining voltage limits. Subsequently, the vanes will be modulated and tests with beam performed.

The authors gratefully acknowledge numerous helpful conversations with Rolf Muller, Jerry Nolen, and John Staples. John Vincent, John Brandon, and other staff members of the National Cyclotron Laboratory made possible the high power RF tests, which were performed at Michigan State University. We also thank Michael Bruns for performing the RELAX 3D calculations.

[1] J. A. Nolen, in the Proc. 1995 IEEE Particle Accelerator Conference, May 1-5, Dallas, Texas, 95CH35843, p354 (1996).

[2] K. W. Shepard and J. W. Kim, in the Proc. 1995 IEEE Particle Accelerator Conference, May 1-5, Dallas, Texas, 95CH35843, p1128 (1996).

[3] R. C. Pardo, et al.,, in the Proc. 1992 Linear Accelerator Conference, August 24-28, Ottawa, Ontario, AECL-10728, p70 (1992).

[4] R. W. Muller, GSI Report GSI-90-25-ISSN 0171-4546, (1990).

[5] John Staples, in the Proc. of the Workshop on Post-Accelerator Issues at the Isospin Laboratory, Berkeley, CA, October 22-29, 1993, edited by S. Chattopadhyay and J. M. Nitschke, P101 (1994).

[6] F. J. Lynch, R. N. Lewis, L. M. Bollinger, W. Henning, and O. D. Despe, Nucl. Instr. and Meth. 159, p245 (1979).

[7] W. D. Kilpatrick, Rev. Sci. Instr. 28, p824 (1957).