A.P. Letchford
Rutherford Appleton Laboratory, Chilton, Didcot, UK
A critical part of the design of a high intensity linear accelerator is to keep activation caused by particle loss below an acceptable limit. For bunch currents up to 200 mA it is possible to make a technical layout of a proton linac which allows operation in a non-space charge dominated regime. As a consequence almost no rms emittance increase is obtained in all three planes and the production of halo particles is reduced. A cylindrical bunch stays cylindrical. To examine the process of particles moving from the core into the halo, Monte Carlo simulations with a large number of macroparticles are necessary. Strong transverse-longitudinal coupling is observed. The simulation results are used also to study the effect of halo scraping.
High intensity proton linacs can either be pulsed H--accelerators up to 5 MW average beam power [1] or cw H+-accelerators up to 130 MW beam power [2]. The major design problem is to reduce the particle loss along the linac down to 1 W/m which corresponds to a loss rate below 10-7 /m. Losses above this limit prevent hands on maintenance. Therefore the linac design is determined by approaching these loss figures.
Particle loss is caused by a small number of particles outside the dense beam core, called the beam halo. The origin and the formation of the halo and its dynamics is an important issue for understanding the particle loss. There exist two different approaches. The first is a theoretical one based on simplified particle distributions and transport channels. Significant progress has been made in recent years on the basis of the so-called 'particle-core model' [3]. However, it is not obvious how to transform those results into loss rates for realistic linac designs where the beam is bunched and accelerated. The other approach is to first set up a realistic linac design based on technical parameters. With the help of Monte Carlo simulations such a design is checked against particle loss.
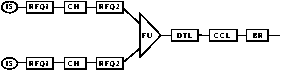
For this investigation of halo properties the underlying realistic high current linac design is the linac of the European Spallation Source (ESS) [4]. The layout of the linac [5] is shown in Fig. 1.
The low energy part consists of two H--ion sources with 70 mA peak current each, two RFQs separated by a 2 MeV bunched beam transfer line for installing a fast chopping device and a 5 MeV funneling line after the second RFQ. The drift tube linac (DTL) operates at 350 MHz and accelerates a bunch current of 107 mA up to 70 MeV. The coupled cavity linac (CCL) has a frequency of 700 MHz resulting in an effective bunch current of 214 mA [6]. The CCL accelerates the beam up to 1.334 GeV. It is followed by a transfer line to the two compressor rings. The linac operates at 50 Hz and 6% duty cycle.
The main task of the linac design is to reduce the losses along the linac and at ring injection [7]. For low loss ring injection the low energy chopper and a bunch rotator in the transfer line are foreseen. The transverse losses along the linac have to be minimized by choosing appropriate parameters.
Beam currents of 107 mA in the DTL and 214 mA in the CCL are considered to be high and therefore it is expected that the beam is space charge dominated. Nevertheless, despite the high current it is possible to set the parameters for the CCL such that the beam dynamics is not space charge dominated, which reduces the sensitivity against mismatch and tolerances.
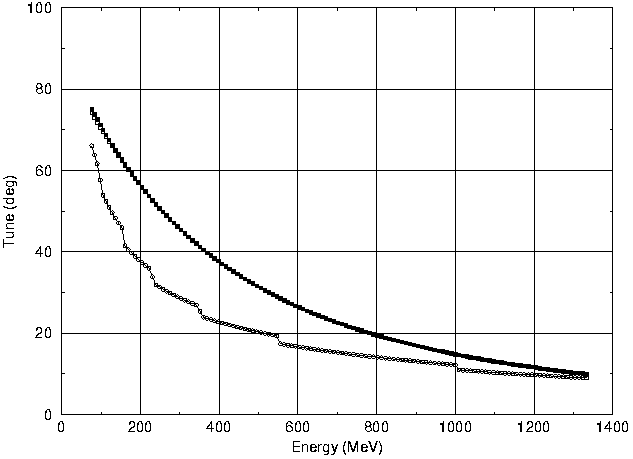
To get a non-space charge dominated design the transverse tune has to
be decreased along the CCL with increasing energy. This increases
the beam dimensions at higher energies giving a smaller space charge
density. As a consequence longitudinal focusing is still effective
at high energies. The energy dependence of the transverse tune 
t in
the CCL is shown in Fig. 2. The transverse tune has been chosen to
decrease like t = to(
/o)-2.5. Here is the relativistic factor and
the index o refers to the input energy of 70 MeV. Other underlying
numbers are the effective beam current of 214 mA, a transverse rms
input emittance of 0.6 
mm mrad and a longitudinal rms input emittance
of 1.2 o MeV. Transverse focusing is provided by doublets.
The tune ratios /o stay rather constant around 0.8 in the transverse
and the longitudinal direction. The value 0.8 is indicative of the
non-space charge dominated design. Not shown is the zero current tune
to. For the CCL design to starts at 105o at 70 MeV. However, to
decreases quite fast. At 105 MeV its value has fallen below 90o. The
longitudinal zero current tune lo is always below 90o.
The equipartition ratio in the bunch system, the ratio between transverse and longitudinal energy, is around 0.5 at the input. As a function of energy the ratio first increases up to 0.9 and then falls down to 0.5 at the high energy end. A ratio of 1 at high energies would be possible by doubling the transverse tune and therefore reducing the transverse beam radius. The increasing space charge density would shift the design parameters into a space charge dominated region [8], which we try to avoid.
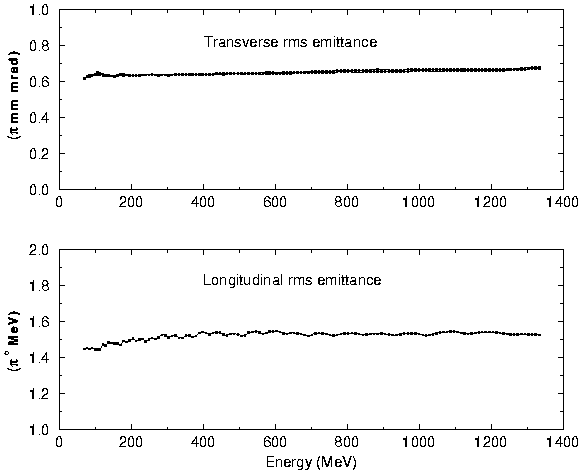
Monte Carlo simulation with up to 200000 particles have been carried through for the DTL and CCL. Hereby the DTL and CCL have been simulated as whole. No effect can be associated with the frequency jump and the change from a singlet to a doublet focusing system. The rms emittances along the CCL are shown in Fig. 3. Less than 10% rms emittance growth is observed. This indicates that no dangerous resonances are present and no temperature exchange takes place between the transverse and the longitudinal direction.
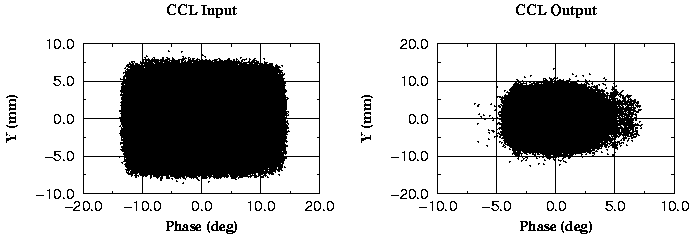
Real space projections at the beginning and at the end of the CCL are shown in Fig. 4. At the input into the DTL the transverse and longitudinal phase space is filled independently with waterbag distributions. This is a reasonable assumption for the particle distribution produced by the preceding RFQ. The resulting cylindrical bunch shape is conserved along the linac. The forces of such a distribution can be calculated analytically [9].
The transverse mismatch factor, which is not shown, has an average value of 0.3. Sources of mismatch are the changes of cell length and number of cells from cavity to cavity. The mismatch causes no rms emittance growth. In summary it can be said that the ESS linac is an example of a high current linac designed in the non-space charge dominated regime. This results in small rms emittance growth, conservation of the bunch shape and in less sensitivity against mismatch.
It is understood that the halo consist of only a small number of particles outside the beam core. Small means that less than 10-3 particles are forming the halo. To understand the properties and dynamic of the halo particles one should try to answer questions about the halo production mechanism and the single particle motion.
To answer these questions Monte-Carlo simulations with a large number of particles here up to 200000, have been made for the ESS Linac, a realistically designed linear accelerator. Results presented here refer to the CCL. The output distribution of the preceding DTL was transferred into the CCL. Space charge calculations are fully three dimensional and no symmetries have been assumed. Projections of the input distribution are shown in Fig. 5. Examining the distribution one can see that no halo has developed up to the end of the DTL. This is no longer true at the end of the CCL, see Fig. 6. Transversely less than 0.1% of the particles have entered the halo. A filamentation is seen in the longitudinal phase space which contains less than 1% of the particles.
The evolution in the longitudinal phase space is shown in Fig. 7 at four different energies along the linac. The boundary of the longitudinal distribution at input differs slightly from an elliptical one. This is due to a 20 % rms emittance increase in the DTL. In order to study the sensitivity against longitudinal mismatch we have not corrected the injection parameters longitudinally. The non-elliptical distribution is connected with nonlinear forces which causes the filamentation in the longitudinal phase space. The mismatch enhances the development of a halo. This agrees with investigations made before [10]. Monte Carlo simulations with a longitudinally matched beam show much less filamentation [11]. While the filamentation is acceptable for the linac, it cannot be ignored in a following high ß transfer line either to a compressor ring or to a target station [12].
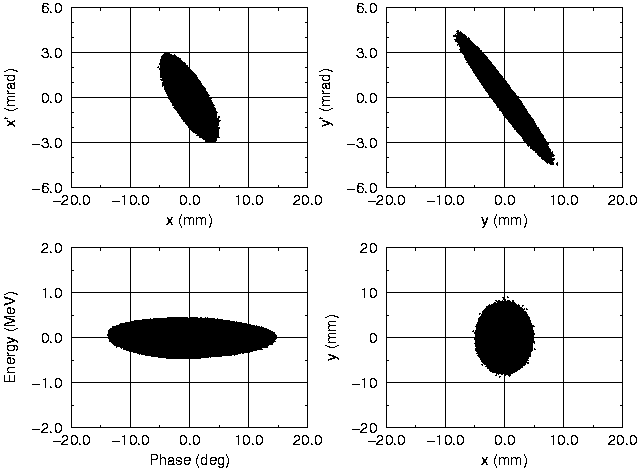
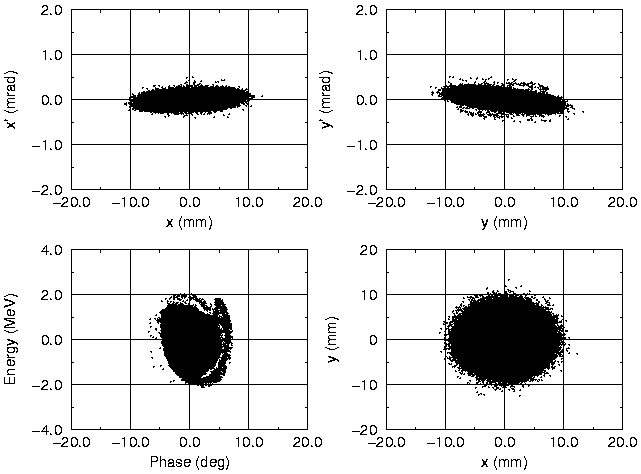
Fig. 6 Phase space projection at the end of the CCL (1.334 GeV)
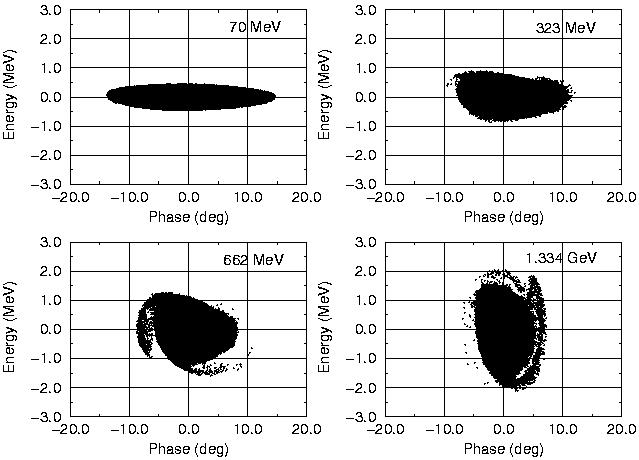
Fig. 7 The evolution of the longitudinal phase
space distribution along the CCL
While we studied the filamentation in the longitudinal phase space, transversely we are interested in the particle motion of the radially outermost particles. The particle-core model assumes that halo particles are oscillating through the beam core [13,14]. For a space charge dominated beam, chaotic particle trajectories have been found [15,16]. Analytical models for halo formation have been developed by different groups [17,18,19] and are confirmed by numerical simulations [19,20].
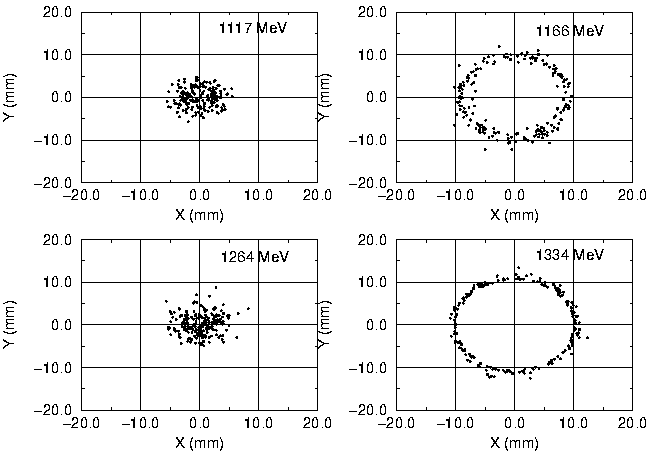
In order to compare the particle-core model with the results of the
Monte Carlo simulation presented here Fig. 8 shows the real space
(x,y) at four different energies. 200 selected particles are plotted
, the outermost ones at the CCL output. Tracing those particles
backwards one sees that the particles are inside the beam core around
1264 MeV. They are in the halo around 1166 MeV and again in the beam
core at 1117 MeV . This corresponds to a full betatron oscillation
consistent with a design tune design tune
t is around 15o at this
energy range. This confirms the particle oscillation predicted by
the particle-core model.
Information about the halo production mechanism can be obtained if the position of halo particles at the CCL input are studied. Again the 200 outermost particles in the (x,y)-space at the end of the CCL are investigated, see Fig. 9. Their positions in phase space at injection are shown in Fig. 10. Comparing Fig. 9 and 10 several conclusions can be made.
Halo particles in (x,y)-space at the end of the CCL come from the boundary of the longitudinal distribution and transversely mainly from the inner part of beam at injection, see Fig. 10. The conclusion cannot simply be reversed. Not every particle which is initially located at the boundary of the longitudinal distribution and inside the beam will become later on a halo particle. All six initial coordinates in the whole phase space have to be considered. At the end of the CCL the same halo particles are found inside the longitudinal phase space distribution forming some clusters, see Fig. 9. In the transverse phase space the particles are uniformly distributed inside the core, see again Fig. 9.
These observations lead to the following conclusion. Radial halo particles are driven out of the beam by a transverse-longitudinal coupling force. Initially they are located at the boundary of the longitudinal phase space projection. The coupling causes the particles to enter the halo in (x,y)-space and at the same time the particles move inwards into the longitudinal distribution. Details of the amount of halo particles in the (x,y)-space at the end of the linac are correlated to the precise knowledge of the longitudinal input distribution.
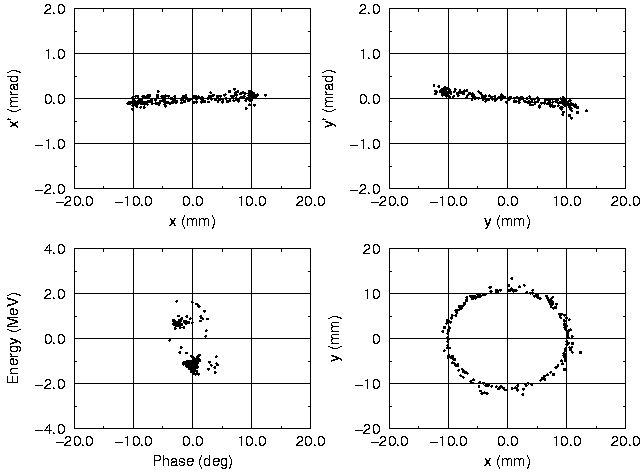
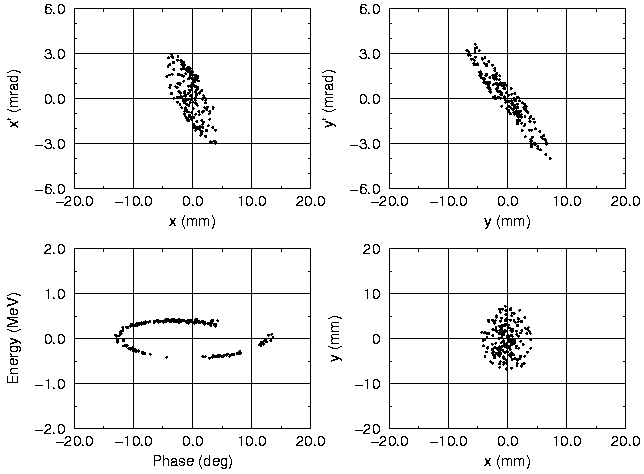
Fig. 10 Phase space distributions of the same particles as in
Fig. 9 at the beginning of the CCL
Summing up, we come to the following explanation for the formation of the halo. The non uniform space charge density of a bunched beam is connected with nonlinear forces and coupling forces between the transverse and longitudinal direction. These forces are the driving terms for the generation of the halo. The transverse-longitudinal coupling cannot be neglected for understanding the properties of the radial halo particles. Mismatch, tolerances and errors are not additional sources, they just enhance the formation of the halo.
Beam envelopes in y-direction are plotted along the linac in Fig. 11.
There are less than 10-4 particles outside 
10 mm for all parts of
the linac, except for two 'hot spots' at around 1150 and 1250 MeV.
The envelope of the outermost particle, representing the 10-5 - level,
reaches values up 15 mm. The pipe radius is 22 mm along the CCL.
Scraping away some particles in the halo at medium energies is tried for the CCL. Around 800 MeV scrapers in the x and y directions are positioned at two places. The distance from the axis is set to be 9 mm. The maximum absorbed beam power is limited to less than 0.5 kW on each scraping device. This corresponds to 30 particles at 800 MeV in a Monte Carlo simulation with 200000 particles.
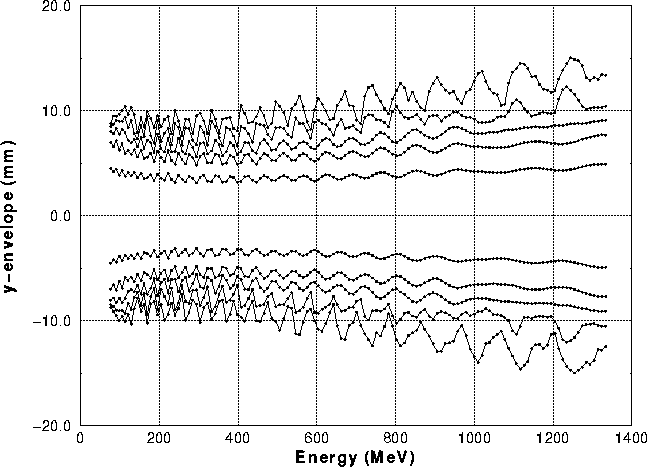
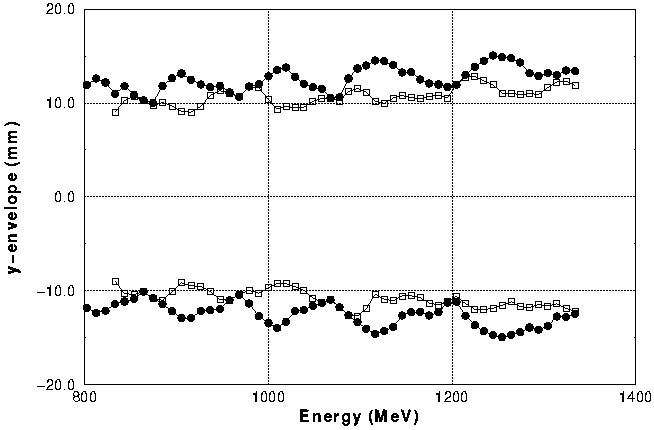
Fig. 12 Beam envelope of the outermost particle without and with two
scrapers. The two outer curves (filled circles)
correspond to the unscraped beam, the two inner ones
(open squares) correspond to the scraped beam.
In Fig. 12 the envelope of the outermost particle in y-direction is
plotted above 800 MeV. Less than 10-3 particles in total are scraped
away. Also shown is the effect of using two scrapers which are
separated by about 40o in betatron oscillation. Quite obvious is the
limitation of the beam envelope to about 10 mm at most positions.
At the two hot spots the number of particles outside 10 mm and the
maximum amplitude are reduced.
The two scrapers are positioned to get an overall 'global' effect on
the beam envelope. For reducing the hot spots other scraper positions
and probably more than two maybe necessary. For the ESS CCL 6 to
8 scrapers in the x and y direction each are considered in every
second diagnostic section, which are separated by about 20o in betatron
oscillation. With this arrangement it should be possible to have less
than 10-5 particles outside 10 mm all along the linac after scraping,
which is a reduction by one order of magnitude.
Greatly acknowledged is the generous provision of computing time by the Forschungszentrum Jülich GmbH. We express our gratitude to N. Attig and R. Vogelsang for helpful discussions and their support in developing the computer programs.
[1] Y. Yamazaki, "Design Issues for High Intensity, High Energy Proton Accelerators", these proceedings
[2] M. Prome, "Major Projects for the Use of High Power Linacs", these proceedings
[3] J. - M. Lagniel, "Halos and Chaos in Space-Charge Dominated Beams", Proc. EPAC Sitges, Spain, 1996
[4] Outline Design for the European Spallation Source, eds: I. S. K. Gardner, H. Lengeler, G. H. Rees, ESS report 95-30-M, Sep. 1995
[5] H. Klein, Transmutation Workshop, Las Vegas 1994, P. 322
[6] M. Pabst, K. Bongardt, Proc. PAC Dallas 1995, p. 3197
[7] K. Bongardt, M. Pabst, "Accelerator Physics of High Intensity Proton Linacs", see ref.3
[8] M. Reiser, N. Brown, Phys. Rev. Lett., vol. 74, p. 1111, 1995
[9] M. de Magistris, V. G. Vaccaro, L. Verolino, "Bunched Beams in Axissymmetric Systems", submitted to Il Nuovo Cimento
[10] C. Chen and R. A. Jameson, Phys. Rev. E, vol. 52, p. 3074, 1995
[11] M. Pabst, K. Bongardt and A. P. Letchford, " Critical Beam Dynamical Issues in Neutron Spallation Sources", Proc. of the 8th ICFA Advanced Beam Dynamics Workshop, Bloomington, USA, Oct. 1995
[12] K. Bongardt, M. Pabst, A. P. Letchford, V. G. Vaccaro, L. Verlino, "Filamentation Effects and Image Charges in High ß Proton Transfer Lines", see ref. 3
[13] J. S. O'Connell, T. P. Wangler, R. S. Mills and K. R. Crandall, Proc. PAC Washington 1993, p. 3657
[14] R. A. Jameson, see ref. 13, p. 3926
[15] J. - M. Lagniel, see ref. 11
[16] A. Piquemal, "About Self-Similarity or Routes to Reversibility in Space Charge Dominated Beams", see ref. 3
[17] R. L. Gluckstern, Phys. Rev. Lett., vol. 73, p. 1247, 1994
[18] A. Riabko et al., Phys. Rev. E, vol. 51, p. 3529, 1995
[19] see also contributions to the 8th ICFA Advanced Beam Dynamics Workshop, Bloomington, USA, Oct. 1995
[20] R. D. Ryne, S. Habib, T. P. Wangler, Proc. PAC Dallas, 1995, p. 3149