While time-dependent electromagnetic fields using microwave technology have been exploited for decades in acceleration and manipulation of charged particle beams, modern lasers stand poised to be exploited for these purposes with great promise. The advent of compact sub-picosecond terawatt lasers has renewed the interest in phenomena that involve scattering or collective interaction of lasers with relativistic particles for various purposes such as diagnostics and control of beams, ultra-high gradient particle acceleration, laser-driven high brightness particle sources, etc. We will give examples of laser-linac interaction already in use or being contemplated in such areas as TeV-scale gamma-gamma colliders, laser monitoring of beams, laser injectors and prospects for laser acceleration of particles.

The microwave technology at frequencies up to tens of GHz has been the work horse for particle accelerators since World War I and II. Powerful radio frequency (rf) electromagnetic energy sources - such as tetrodes and klystrons, with a great deal of flexibility in amplitude, phase and frequency control - have been the drivers of particle storage and acceleration in circular and linear accelerators. Along with such versatile power sources came the necessity to control and manipulate particle beams via rf electromagnetic fields to a high degree of precision. The rf and beam feedback systems, bunch-rotating and Landau rf cavities, etc. - all have been employed successfully to benefit collider operation. As the science and technology of rf sources and devices progressed, the demands on the spectral purity of rf components for accelerator applications rose precipitously. This has been so in order to assure a high degree of stability and control of the beam.

Progress in technology allows us today to contemplate going beyond the GHz microwave rf technology to mm-wave and even THz radiation sources and eventually to the state-of-the-art short pulse high power compact lasers. Many of these technologies are ready to be exploited in charged particle handling devices. In this article, we will restrict ourselves to various possibilities with lasers only, and even that as it applies to possibilities with linear accelerators alone, leaving untouched the multitude of possibilities with storage rings and circular colliders.

The development of compact high power, short pulse, efficient lasers is a fast moving technology [1]. Peak powers well above multiple terawatts have been demonstrated and routinely used in the so-called Table Top Terawatt (T3) solid state lasers, based on the Chirped Pulse Amplification (CPA) technique. Current research is focused on further increase of peak power (multiple Joules of energy in sub 100 fs pulse length) as well as increasing the repetition rate beyond 1 Hz to a kHz and beyond. This latter aspect of high repetition rate as well as the phase, amplitude and jitter control of T3 lasers is very relevant for particle accelerators. Fortunately, we benefit from the laser developments driven by the demands for coherent control needed for research in fields such as ultrafast phenomena in solids, chemistry of liquid and gas phases and many biological studies.

These intense lasers are well-known to have high electric and magnetic fields. Investigations are under way throughout the world to explore possibilities to exploit such intrinsic ultrahigh electromagnetic fields by coupling these lasers appropriately to a particle beam for net longitudinal acceleration and for other beam manipulations [2-3]. Such coupling can be produced in free space in presence of suitable boundaries and apertures; or in free space without boundaries via nonlinear higher order mechanisms and in presence of magnetic fields; or via direct coupling to a suitable macroscopic medium like a plasma. However, just as in today's microwave technology involving beam manipulation over fractions of 'mms' in time-scales of 'picoseconds' at frequencies of 'GHz', one would have to invent techniques and learn to manipulate and control signals and particles at optical wavelengths of 'microns', in time-scales of 'femtoseconds' and at frequencies of 'THz' in order to take advantage of today's lasers.

Lasers can be scattered off a relativistic electron beam and the frequency up-shifted photons can be used directly for various scientific applications. One such use of lasers in linear accelerators is in the realm of colliders where a linear - or photon-photon collider provides an attractive complement to high energy TeV scale electron-positron collisions. This is discussed in Section II. The intrinsic coherent transverse focal volume of a laser is typically much smaller than that of a particle beam. Thus lasers could act as ideal microprobes of particle beam phase space for purposes of diagnostics. This is discussed in Section III. One particular aspect that makes lasers unique is their ultrashort pulse duration (100 fs or shorter) which makes time-resolved measurements of emittance over short beam slices possible. The intrinsic high field of lasers allow us to contemplate their use in particle acceleration and various beam manipulations. This is discussed in Section IV. Finally the tunability and short pulse nature together with the ability to synchronize lasers to sub-ps level make them ideal drivers for particle injectors to linear accelerators. Various possibilities are under investigation and are reported in Section V. Section VI concludes with an outlook.

The LEP and the SLC have been successful in doing precise spectroscopy of the W± and Z0. However, we understand the technical and fiscal constraints of large circular lepton colliders owing to limits imposed by the synchrotron radiation. Hence, there is increasing interest world-wide in TeV scale linear colliders involving electrons and positrons. Such colliders are seen as complementing the multi-ten TeV hadron colliders of the future, such as the LHC.

It has also been recognized that in order to maximize the reach to accessible high energy physics frontier, it is important and reasonable to explore the technical possibility of at least two interaction points (IPs) at these colliders: one for normal electron-positron collisions and a second one for collisions of hard photons on hard photons, electrons on hard photons and electrons on electrons. This second IP is commonly referred to as the Gamma-Gamma Collider arm of a linear collider - a term dubbed after an international workshop on the topic in Berkeley in 1994 [4]. High energy photons i.e. gamma rays for these collisions are most effectively produced via Compton backscattering of focused laser beams by the high energy electron beams of the linear collider. The high energy photon beams are then brought into collision with opposing electron or photon beams. Since one does not need positrons for the Compton conversion, the possibility of electron-electron collision exist as well. With suitable laser and electron beam parameters, a luminosity of electron-photon and photon-photon collisions comparable to that of the electron-positron collisions can be achieved. In addition, the polarization of the high energy photons can be controlled via polarization of the laser and the electron beams. With high luminosity and variable polarization, the photon-photon and electron-photon collisions at TeV energies will significantly enhance the discovery potential and analytic power of a TeV linear collider complex.

Yet another important reason to consider photon-photon collisions is the limitations imposed by radiative effects of the macroscopic beam electromagnetic fields. Charged particles get bent severely by the macroscopic electromagnetic field of the opposing colliding beam, leading to copious emission of what is known as 'beamstrahlung' photons, characterized by the parameter - a classical measure of average radiated photon energy in units of beam particle energy. The effect also leads to a large energy spread, _B, in the colliding beams. If the number of particles per colliding bunch is too large, the beamstrahlung photons can produce coherent pairs, causing concern about electromagnetic and hadronic backgrounds in the detector. Typically, the conventional wisdom in collider design is to stay below ~0.3 limit in order not to be limited by the radiative effects. However, as one reaches up to higher energies of 5 TeV in the center-of-mass and beyond with luminosities above 1035 cm-2 s-1, conventional choices for the radiative effects lead to unrealistic values for critical collider parameters e.g. a total site power well above a gigawatt, etc. We are thus forced to consider colliders with radiative parameters in the unconventional regime of °>>0.3 and large _B. The "-" collisions (instead of direct e+e- collisions) via Compton conversion offer an alternative paradigm to collider physics, with no limitation from beamstrahlung or coherent pair production. The issues to be addressed are rather different: the development of suitable laser technology, the feasibility of the laser-beam and interaction point geometry and the complementarily of the physics.

A preliminary but rapidly evolving conception of such a composite and integrated linear collider complex is being considered by the international linear collider community at present and is shown in Figure 1 [5]. The required laser peak powers - about a Joule in a picosecond or a 100 mJ in 100 femtoseconds - have already been achieved in today's state-of-the-art T3 lasers. And there is significant promise of enhanced repetition rate operation of these lasers to match the particle beam collision frequency for luminosity considerations. Investigations on both conventional lasers and Free Electron Lasers (FELs) towards this goal are underway at present [5].

Fig. 1 A linear collider configuration with electron-positron, photon-photon, electron-photon, and electron-electron collisions.

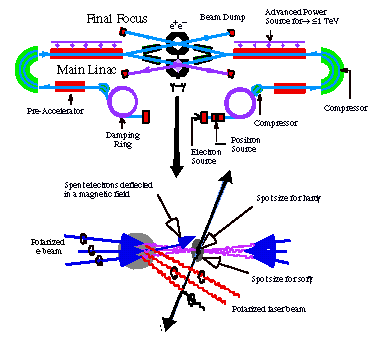
The TeV-scale electron-positron -gamma linear colliders envisioned today would require beam spot sizes of nanometers at the final focus of the collisions. For controlling the collisions and maintaining the luminosity, it is critical that one is able to measure and monitor such ultra-small spot sizes. Lasers have already been employed in this task successfully at the SLC at SLAC [6].

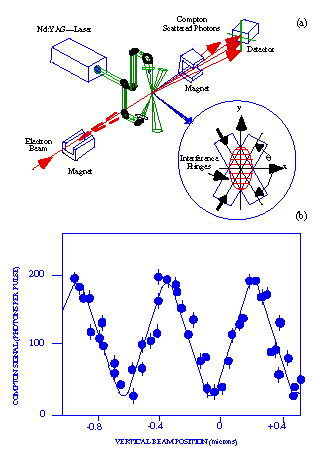
The principle of small spot-size measurement at the SLC is illustrated in Figure 2 (a) below. An interference fringe or standing wave pattern is created by direct and reflected near-infrared laser beams orthogonal to the electron beam. The relativistic electron beam is scanned across the waist of the fringe pattern. The pattern created by the Compton-scattered photons at a detector along the beam's forward direction has intensity oscillations as a function of beam position during scanning, as shown in Figure 2 (b) for the SLC. The result contains information about the beam size, resulting in a measure spot size of 70 nm!

Fig. 2 (a) and (b) Final spot size measurement at the SLC via Compton Scattering across laser interference frignes.

While monitoring and control of beam spot sizes are important, the longitudinally time-resolved measurement of beam phase-space characteristics are even more critical. Development of this kind of techniques will become increasingly necessary for diagnosing electron bunches in future accelerators. Since the transverse coherence volume of lasers is typically much smaller than that of a particle beam, the laser beam can act as an optical microprobe of a finite region of the beam transverse phase space and with the advent of femtosecond lasers, all this can be achieved in a time-resolved manner over femtosecond slices of many samples of a beam.

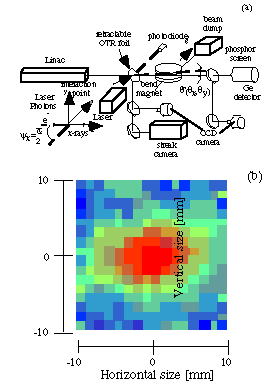
X-rays produced by Thomson scattering of a short terawatt laser pulse (40 mJ, 100 fs long) off a 50 MeV electron beam at 90_ have already been shown to be an effective diagnostic to measure transverse and longitudinal density distribution of the electron beam with subpicosecond time resolution at the Beam Test Facility at LBNL [7]. Near- infrared (800 nm) laser pulses, were focused onto the electron beam waist, generating x-rays in the forward direction with energies up to 30 keV (Figure 3 (a)). The transverse and longitudinal electron beam dimensions have been obtained by measuring the intensity of the x-ray beam, while scanning the laser beam across the electron beam in space and time (Figure 3 (b)). The electron beam divergence or transverse momentum distribution has been obtained through intensity and size measurement, followed by a deconvolution of spatial and spectral characteristics of the scattered x-ray beam, thus completing the full transverse phase-space characterization of the electron-beam in steps of femtoseconds over its entire 20 ps duration.

Fig.3 (a) and (b) Thomson scattering phase-space diagnostic set-up (a) and phosphor image of scattered x-rays (b).

It is well known that lasers have inherently high electric and magnetic fields, that can potentially be harnessed for compact ultra-high gradient linear accelerators. There exists the possibility of acceleration via lasers in free space in presence of suitable boundaries or via nonlinear higher order mechanisms or via direct coupling of lasers to a plasma-like medium [2-3]. Among experimental results to date on laser-driven acceleration of electrons in a plasma, the UK (RAL) experiment is the most recent (1996). It has demonstrated the highest gradient (100 GV/m) and produced beam-like properties in the accelerated electrons with 107 electrons @ 40 MeV ± 10% with a normalized emittance of eN<5 mm-mrad [8].

I would like to remind the readers of two important aspects that will critically determine the future of laser acceleration schemes. First, just as today's microwaves from klystrons are suitably guided by linac waveguide structures without diffraction for efficient coupling to a charged particle beam, we will have to learn how to focus strongly (in order to achieve high electric field intensities) and simultaneously guide short pulse high energy lasers over long macroscopic distances of cms without diffraction in order to use them for particle acceleration. Second, one would have to master the relative amplitude, phase and frequency control of lasers similar to that exhibited by today's rf control level, but scaled to laser frequencies.

An artist's impression of a staged and modular laser wakefield accelerator, compared and contrasted to its present-day microwave linac analog, is depicted in Figure 4 [9]. Such a scheme depends on the success of propagating and guiding intense laser pulses in hollow plasma channels at high power densities of the order of 1018 W/cm2 over several hundred Rayleigh lengths. I would like to mention here the important results obtained at Maryland [10], where lasers focussed to 1014 Watts/cm2, have been propagated up to 70 Rayleigh lengths. Much progress has also been made in the context of pulse train generation and control in today's table-top terawatt lasers, thanks to applications in coherent wavepacket control for studies in chemistry. One has the capability today of tailoring a sequences of up to eight or ten pulses, varying in strength, phase and width from a short pulse laser.

Fig. 4 Conventional microwave linac (a) with klystrons and metallic waveguides vs. conceptual laser-plasma linac (b) with lasers and plasma guides.

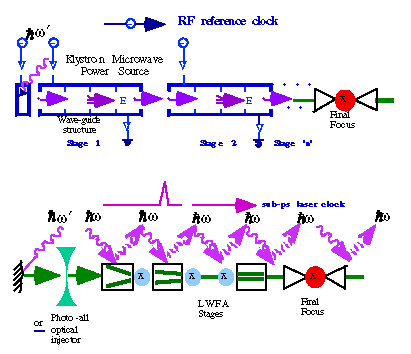
A state-of-the-art T3 - laser with improved repetition rate (10TW, 300 fs, 10 kHz) will provide 3 J of laser energy per pulse at a wavelength of 1 µm. If one aims at a 1 meter stage with energy gain of 10 GeV, one needs a plasma 1 meter long, with a density of 1017 cm-3 accommodating 300 Rayleigh lengths. The accelerating wakefield wavelength will be 100 µm, the channel radius 30 µm, the acceleration gradient of 10 GV/m, with channel density variation of a 50% from center to the edge. In this scenario, one laser creates the necessary plasma acceleration structure via guiding, the other creates the wakefield for acceleration.

The required plasma channels need further study in order to overcome diffraction and to decouple the transverse gradient from that of the accelerating wake. Many similarities exist between linac structures and hollow plasma guides. These need to be quantified and better understood. Synchronization of laser and electron pulse from stage-to-stage in Figure 4 demands sub-ps laser synchronization scheme. There are various injection and synchronization schemes under study at present as mentioned in Section V.

Should the guiding, staging and controllability issues be worked out, there is hope that wakefields excited in plasmas by a suitably shaped laser pulse will have the necessary characteristics for particle acceleration to ultrahigh energies, based on rather reliable simulations available today [11].

Lasers are beginning to play a crucial role in injectors of high quality (i.e. low emittance and high phase-space brightness) electron beams to linear accelerators. RF photoinjectors, where electrons packed tightly in phase-space are produced from a photocathode surface properly embedded in a high electromagnetic field inside a radio frequency cavity and subjected to short pulse laser irradiation for photo-emission, have been under intensive development in the past decade. Normalized particle beam emittances close to 1 mm-mrad have been achieved. .Such optically switched rf photoinjectors are optimal candidates as injectors for FELs and future colliders based on metallic traveling waveguide linear accelerators. The promise and R&D of rf photoinjectors is described elsewhere in detail [12].

As we have discussed before, some of the high gradient acceleration concepts using lasers as drivers envision using a high density (1014-1018 cm-3) plasma as an accelerating structure over the short time duration of a picosecond or so [2-3]. For possible future high gradient linear accelerators based on laser-driven plasmas, it is probably more natural to consider a photoinjector that is based on a plasma, rather than on a rf cavity made up of conducting metallic structures. 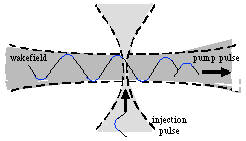Thus emerges the concept of LILAC - Laser Injected Laser ACcelerator, proposed by D. Umstadter [13]. In LILAC, one laser pulse drives a wakefield in the plasma and another ejects and injects background plasma electrons, thus employing an all-optical synchronized injection and acceleration (Figure 5). In laboratory experiments, a terawatt-peak-power laser beam was focused into a gas jet and an electron plasma wave was observed to create and accelerate a naturally collimated beam of electrons in a 10 fs slice to relativistic energies (up to 109 electrons, with an energy distribution maximizing at a MeV and a physical (unnormalized) total geometric transverse emittance of 1 mm-mrad and electric field gradient of 2 GV/cm) [13].

Yet another laser-based, ultra-cold optical injector scheme is based on interaction of subcyclic optical pulses with a thin plasma film (10 nm in thickness) [14]. The resulting chirp introduced in the electron phase space of the plasma distribution leads to a compressed ultracold electron bunch with a potential normalized emittance of 10-3 mm-mrad in a bunch shorter than a nm. It is important to note however that such a short bunch will radiate coherently (N2 radiation) in soft x-ray and longer wavelengths.

Finally, Pellegrini [15] has proposed a FEL solution to the injection into a plasma-based accelerator. Such accelerators typically demand an injector pulse as long as a tenth of the plasma wake wavelength and a normalized emittance less than 1 p mm-mrad for focussing into an optical channel. The scheme is based on using the same laser to drive the plasma accelerator and to seed a FEL modulation into the injected beam from a rf photoinjector. The FEL, thus phase-locked to the plasma wave will provide both longitudinal and transverse focusing and a train of synchronized bunches.

Fig. 5 The LILAC concept: one pulse drives a wakefield and another injects electrons.

There is significant promise of the usefulness of lasers in the monitoring, control and manipulation of charged particle beams. The time is ripe to begin exploiting today's lasers and even guide its future development for this purpose.

The author wishes to thank "Sam" Vanecek for producing the graphics in this paper.

[1] G. Mourou, "Laser for Wakefield Plasma Accelerator", in The Future of Accelerator Physics, The Tamura Symposium Proceedings, Nov. 1994, AIP Conf. Proc. 356, pp. 301-309.

[2] The Future of Accelerator Physics, The Tamura Symposium Proceedings, Nov. 1994, AIP Conf. Proc. 356.

[3] Advance Accelerator Concepts, AIP Conf. Proc. 335, 1994.

[4] S. Chattopadhyay and A. Sessler ed., Proceeding of the Workshop on Gamma-Gamma Colliders, Berkeley, CA, March 1994, Nucl. Instr. Meth. in Physic Res., Feb. 1, 1995, Vol. 355, No. 1, pp. 1-194.

[5] Zeroth-Order Design Report for the Next Linear Collider, LBNL-PUB-5424, SLAC Report 474, UCRL-ID-124161, Vol. 2., pp. 971-1030.

[6] B. Schwarzchild, "New Stanford Facility Squeezed High-Energy Electron Beams", Physics Today, July 1994, p. 22.

[7] W. Leemans et. al., "X-ray based sub-picosecond electron bunch characterization using 90_ Thomson scattering", LBNL-39060, submitted to Physical Review Letters, May 1996.

[8] The author acknowledges T. Katsouleas for private conversations on this topic.

[9] The author is indebted to T. Tajima for fruitful discussions on conceptualizing Figure 4.

[10] C. Durfree, et. al., Phys. Rev. Lett. (93); Phys. Rev. E (95).

[11] J. S. Wurtele, "Advance Accelerator Concepts", Physics Today, pp. 33-40 (1994).

[12] J.E. Clendenin, "RF Photoinjectors", these proceedings.

[13] D. Umstadter et. al., "Nonlinear Optics in Relativistic Plasmas and Laser Wake Field Acceleration of Electrons", Science, Vol. 273, pp. 472-475, 26 July 1996.

[14] B. Rau, T. Tajima and H. Hojo, "Ultracold Optical Injector", submitted to Phys. Rev. Lett.

[15] The author is indebted to C. Pellegrini for bringing this work to his attention.