Robert Palmer, Juan Gallardo,
Brookhaven National Laboratory
Upton, NY 11973-5000, USA
Muon Colliders have unique technical and physics advantages
and disadvantages when compared with both hadron and
electron machines. They should be regarded as
complementary. Parameters are given of 4 TeV high
luminosity 
collider, and of a 0.5 TeV lower
luminosity demonstration machine. We discuss the various
systems in such muon colliders.
The possibility of muon colliders was introduced by Skrinsky et al. [1], Neuffer [2], and others. More recently, several workshops and collaboration meetings have greatly increased the level of discussion [3, 4]. A detailed Feasibility Study [5] was presented at Snowmass 96.
Hadron collider energies are limited by their size, and
technical constraints on bending magnetic fields. Lepton
( 
or ) colliders, because they undergo simple,
single-particle interactions, can reach higher energy final
states than an equivalent hadron machine. However,
extension of colliders to multi-TeV energies is
severely performance-constrained by beamstrahlung, The
luminosity 
of a lepton collider can be written:
where 
is the average vertical (assumed smaller) beam
spot size, E is the beam energy, 
is the total
beam power, 
is the electromagnetic constant, 
is the classical radius,
and 
is the number of photons
emitted by one bunch as it passes through the opposite one.
If this number is too large then the beamstrahlung
background of electron pairs and other products becomes
unacceptable.
As the energy rises, the luminosity, for the same event
rate, must rise as the square of the energy. For an electron
collider, 
, and, for a fixed background,
we have the severe requirement:
In a muon collider there are two significant changes: 1)
The classical radius is now that for the muon and is
200 times smaller; and 2) the number of collisions a bunch
can make 
is no longer 1, but is now
related to the average bending field in the muon collider
ring, For 6 T, it is 900.
In addition, with muons, synchrotron radiation is negligible, and the collider is circular. In practice this means that it can be much smaller than a linear electron machine. The linacs for the 0.5 TeV NLC will be 20 km long. The ring for a muon collider of the same energy would be only about 1.2 km circumference.
There are, of course, technical difficulties in making
sufficient muons, cooling and accelerating them before they
decay and dealing with the decay products in the collider
ring. Despite these difficulties, it appears possible that
high energy muon colliders might have luminosities
comparable to or, at energies of several TeV, even higher
than those in colliders.
The basic parameters of a 4 TeV collider are shown
schematically in Fig. 1 and given in
Table 1 together with those for a 0.5 TeV
demonstration machine based on the AGS as an injector. It
is assumed that a demonstration version based on upgrades
of the FERMILAB machines would also be possible.
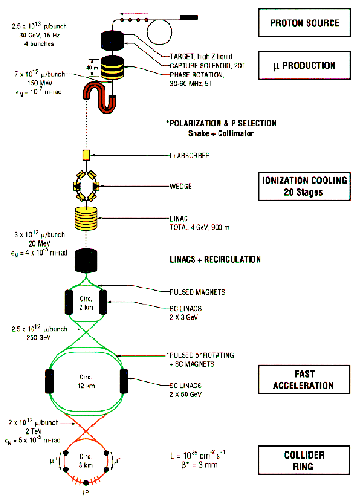
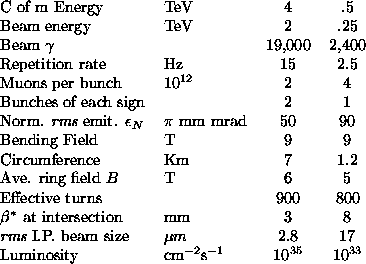
The proton driver is a high-intensity (four bunches of
protons per pulse) 30 GeV proton
synchrotron, operating at a repetition rate of 15 Hz. Two
of the bunches are used to make 
's and two to make
's. Prior to targeting the bunches are compressed to
an rms length of 1 ns.
For a demonstration machine using the AGS [6], two
bunches of 
at a repetition rate of 2.5
Hz at 24 GeV could be used.
Predictions of nuclear Monte-Carlo
programs [7, 8, 9] suggest that 
production is maximized by the use of heavy target
materials, and that the production is peaked at a
relatively low pion energy ( 
MeV),
substantially independent of the initial proton energy.
Cooling requirements dictate that the target be liquid: liquid lead and gallium are under consideration. In order to avoid shock damage to a container, the liquid could be in the form of a jet.
Pions are captured from the target by a high-field (20 T, 15 cm aperture) hybrid magnet: superconducting on the outside, and a water cooled Bitter solenoid on the inside. A preliminary design [10] has a Bitter magnet with an inside coil diameter of 24 cm (space is allowed for a 4 cm heavy metal shield inside the coil) and an outside diameter of 60 cm; it provides half (10 T) of the total field, and would consume approximately 8 MW. The superconducting magnet has a set of three coils, all with inside diameters of 70 cm and is designed to give 10 T at the target and provide the required tapered field to match into the decay channel.
The decay channel consists of a periodic superconducting
solenoidal (5 T and radius 
cm). A linac is
introduced along the decay channel, with frequencies and
phases chosen to deaccelerate the fast particles and
accelerate the slow ones; i.e. to phase rotate the muon
bunch.
Figure 2 shows the energy vs ct at the end of the decay channel.
, and 
are marked by the symbols `+', `.' and `-' respectively.
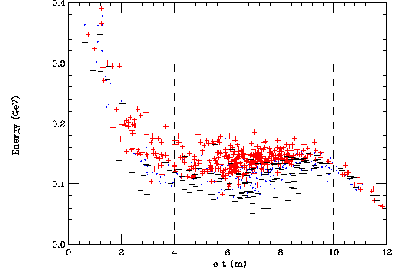
The selected muons have a mean energy 150 MeV,
rms bunch length 
m, and rms momentum spread
% ( 
%,
). The number of
muons per initial proton in this selected bunch is
0.3.
If nothing is done then the average
muon polarization is about
0.19. If higher polarization is desired, some selection of
muons from forward pion decays 
is required. This can be done by momentum
selecting the muons at the end of the decay and phase
rotation channel. A snake [11] is used to generate
the required dispersion. Varying the selected minimum
momentum of the muons yields polarization as a function of
luminosity loss as shown in Fig. 3. Dilutions
introduced in the cooling have been calculated [12]
and are included. A siberian snake is also required in the
final collider ring.
For the required collider luminosity, the phase-space
volume must be greatly reduced; and this must be done
within the 
lifetime. Cooling by synchrotron
radiation, conventional stochastic cooling and conventional
electron cooling are all too slow. Optical stochastic
cooling [13], electron cooling in a plasma
discharge [14] and cooling in a crystal
lattice [15] are being studied, but appear very
difficult. Ionization cooling [16] of muons seems
relatively straightforward.
In ionization cooling, the beam loses both transverse and longitudinal momentum as it passes through a material medium. Subsequently, the longitudinal momentum can be restored by coherent reacceleration, leaving a net loss of transverse momentum.
of muons
accepted;
the dashed line shows
polarization as selected before cooling; the solid line
gives polarization
after cooling.
The equation for transverse cooling (with energies in GeV) is:
where 
is the normalized emittance,
is the betatron function at the absorber,
is the energy loss, and 
is the
radiation length of the material. The first term in this
equation is the coherent cooling term, and the second is
the heating due to multiple scattering. This heating term
is minimized if is small (strong-focusing)
and is large (a low-Z absorber).
Energy spread is reduced by placing a transverse variation in absorber density or thickness at a location where position is energy dependent, i.e. where there is dispersion. The use of such wedges can reduce energy spread, but it simultaneously increases transverse emittance in the direction of the dispersion. It thus allows the exchange of emittance between the longitudinal and transverse directions.
The cooling is obtained in a series of cooling stages. In general, each stage consists of three components with matching sections between them:
's are
minimum.
In a few of the later stages, current carrying lithium
rods replace item (1) above. In this case the rod serves
simultaneously to maintain the low , and
attenuate the beam momenta. Similar lithium rods, with
surface fields of 
T , were developed at Novosibirsk
and have been used as focusing elements at FNAL and
CERN [17].
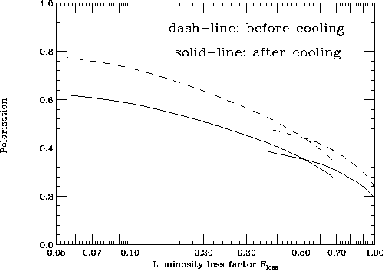
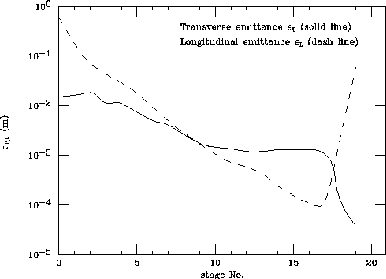
The emittances, transverse and longitudinal, as a function
of stage number, are shown in Fig. 4. In the
first 10 stages, relatively strong wedges are used to
rapidly reduce the longitudinal emittance, while the
transverse emittance is reduced relatively slowly. The
object is to reduce the bunch length, thus allowing the use
of higher frequency and higher gradient rf in the
reacceleration linacs. In the next 7 stages, the
emittances are reduced close to their asymptotic limits. In
the last 3 stages, using lithium rods, there are no wedges
and the energy is allowed to fall to about 15 MeV.
Transverse cooling continues, and the momentum spread is
allowed to rise.
The total length of the system is 750 m, and the total
acceleration used is 5 GeV. The fraction of muons remaining
at the end of the cooling system is calculated to be
%.
Following cooling and initial bunch compression the beams must be rapidly accelerated to full energy (2 TeV, or 250 GeV). A sequence of recirculating accelerators (similar to that used at CEBAF)could be used but would be relatively expensive. A more economical solution would be to use fast pulsed magnets in synchrotrons with rf systems consisting of significant lengths of superconducting linac.
For the final acceleration to 2 TeV in the high energy machine, the power consumed by a ring using only pulsed magnets would be excessive and alternating pulsed and superconducting magnets [18] are used instead.
After acceleration, the and bunches are
injected into a
separate storage ring. The highest possible average
bending field is
desirable to maximize the number of revolutions before
decay, and thus
maximize the luminosity. Collisions occur in one, or
perhaps two, very
low- 
interaction areas.
The magnet design is complicated by the fact that the
's decay within
the rings ( 
), producing
electrons whose mean energy is approximately 0.35 that
of the muons. These
electrons travel toward the inside of the ring dipoles,
radiating a
fraction of their energy as synchrotron radiation
towards the outside of the
ring, and depositing the rest on the inside. The total
average power deposited,
in the ring, in the 4 TeV machine is 13 MW.
The beam must thus be surrounded by a 6 cm
thick warm
shield [19],
which is
located inside a large aperture conventional
superconducting magnet.
The quadrupoles can use warm iron poles placed as close to the beam as practical, with coils either superconducting or warm, as dictated by cost considerations.
In order to maintain a bunch with rms length 3 mm, without excessive rf, an isochronous lattice, of the dispersion wave type [20] is used. For the 3 mm beta at the intersection point, the maximum beta's in both x and y are of the order of 400 km (14 km in the 0.5 TeV machine). Local chromatic correction is essential. Two lattices have been generated [21, 22], one of which [22], after the application of octupole and decapole correctors, has been shown to have an adequate calculated dynamic aperture.
Studies of the resistive wall impedance instabilities indicate that the required muon bunches would be unstable if uncorrected. In any case, the rf requirements to maintain such bunches would be excessive. BNS [23] damping, applied by rf quadrupoles [24], is one possible solution, but needs more careful study.
Monte Carlo study [25, 19] indicated that the background, though serious, should not be impossible. Further reductions are expected as the shielding is optimized, and it should be possible to design detectors that are less sensitive to the neutrons and photons present.
There would also be a background from the presence of a halo of near full energy muons in the circulating beam. The beam will need careful preparation before injection into the collider, and a collimation system will have to be designed to be located on the opposite side of the ring from the detector.
There is a small background from incoherent (i.e.
) pair production in the 4 TeV Collider
case. The cross section is estimated to be 
, which
would give rise to a background of 
electron pairs per bunch crossing. Approximately 90%
of these, will be trapped inside the tungsten nose cone,
but those with energy between 30 and 100 MeV will enter
the detector region.
colliders, and, at higher energies
could be a viable alternative.
This research was supported by the U.S. Department of Energy under Contract No. DE-ACO2-76-CH00016 and DE-AC03-76SF00515.
Colliders and High Energy Storage Rings, Physics
Potential & Development of Colliders. 2 
Workshop, Sausalito, CA, Ed. D. Cline, AIP Press, Woodbury, New York, (1995).
Colliders:
Particle Physics and Design, Napa CA, Nucl Inst. and Meth., A350 (1994;
Proceedings of the Muon Collider Workshop, February 22, 1993, Los Alamos
National Laboratory Report LA- UR-93-866 (1993) and
Physics Potential & Development of Colliders 2
Workshop, Sausalito, CA, Ed. D. Cline, AIP Press, Woodbury, New York, (1995).
Collider
Collaboration Meeting, Feb 6-8, 1995, BNL, compiled by Juan C. Gallardo;
transparencies at the 2 + 2 TeV
Collider Collaboration Meeting, July 11-13, 1995, FERMILAB, compiled by Robert
Noble; Proceedings of the 9th Advanced ICFA Beam Dynamics Workshop, Ed. J.C.
Gallardo, AIP Press, Conference Proceedings 372 (1996).
Collider: A Feasibility Study, BNL-52503,
FermiLab-Conf.-96/092, LBNL-38946, Proceedings of the Snowmass Workshop 96, to
be published.
Colliders, Proc., 3rd
Int. Conf., San Francisco, Dec. 1995, Elsevier, in press.
Colliders
2 Workshop, Sausalito, CA, Ed. D. Cline, AIP Press, Woodbury, New York,
pp. 146 (1995).
Colliders, Proc., 3rd
Int. Conf., San Francisco, Dec. 1995, Elsevier, in press.
Collider, Physics Potential &
Development of Colliders 2 Workshop, Sausalito, CA, Ed. D. Cline,
AIP Press, Woodbury, New York, pp. 178 (1995).
unpublished.
